最小二乘法的数学公式！

吴德辉老师 3583 阅读 0 评论 5 点赞

最小二乘法在很多地方都会用到。比如形状公差中，如果设计者采用下面的标注：

图1 图纸标注

图1中的标注，平面度的理想要素就必须采用最小二乘法拟合出来（如果没有那个G的修饰符号，默认是最大值最小法拟合平面）。还有，很多基准的拟合，也会近似的采用最小二乘法拟合。

之前在公差联盟介绍过最小二乘法，但是有很多好学的小伙伴总是追问，最小二乘法的数学公式究竟是怎么样的？

本期的这一篇文章，我们将介绍一个简洁的最小二乘法数学公式，慢慢剖析它，争取让好学的小伙伴们能认识它，然后再结合Excel利用它来做一些计算。

本期文章将分3个部分来讲解：

1. 3个方程组

2. 矩阵的初步概念

3. 最小二乘法的公式和案例

本期的文章可能会让很多小伙伴感到头疼不适，因为涉及的数学概念较多（主要是线性代数），如果你对线性代数比较了解，可以直接跳到第三节，如果不太了解，建议耐心把它看完。我们尽量从实用的角度出发，避重就轻，尽最大限度帮助小伙伴们快速理解这个公式的含义并学会使用它。

1. 3个方程组

1.1 不定方程组

方程组，我们初中就学过解方程。

我们知道，平面上的直线方程为：

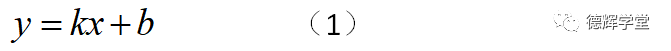
图2 直线方程

比如有一天，老师出的题目是这样的：已知平面中的一个点P（x0, y0)，求过这个点P的直线方程？

注意，直线方程有两个重要的参数，k和b，只要我们知道这两个参数，这个直线方程就确定了。所以我们把这个点P（x0,y0)带入直线方程（1）可得：

上式其实就是一个方程组（只不过方程组里只有一个方程），这里的未知数是k和b。如果根据方程组（2）能够求出k和b, 那么直线方程就求出来了。

问题是，两个未知数，一个方程组，怎么解？显然在方程组(2)中， k和b的解有很多个，不唯一。想象一下就可以理解，平面上，过一个点的直线有无数条，所以k和b的解有很多个。

图3 过一个点有无数条直线

可以看出来，方程组（2）的特点是，方程的个数（也就是已知点的个数）小于未知数的个数（2个）。这样的方程组，我们叫不定方程组，它没有唯一解，有无数个解。

不定方程组对我们的意义在于，如果你用三坐标只采一个点，在没有其它约束的条件下，三坐标是没有办法拟合出一条直线的，因为有无数条直线的可能，三坐标会直接懵逼出错。

当然，不定方程组，有一个唯一的最小范数解，和我们的主题无关，不去管它。

1.2 正定方程组

如果在平面上，有两个已知点：P1(x1, y1), P2(x2,y2), 求过这两个点的直线方程？相信初中班的小家伙们就可以解出来的，因为直接把两个已知点带入直线方程（1），就可以得有两个方程的方程组：

根据方程组（3），我们可以直接解出k和b, 再次强调， k和b是未知数。只要P1和P2不在同一个点上，方程组（3）一定有唯一解k和b。从几何上讲，过P1和P2两点一定有一条唯一直线。

来看看图吧：

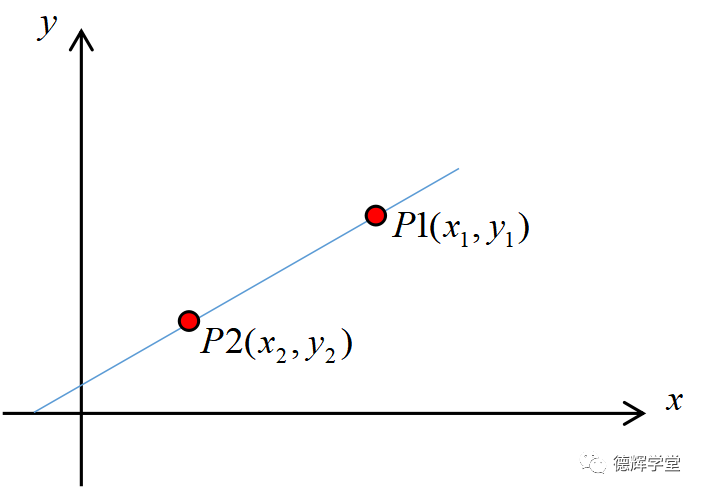
图4 过两个点能确定一条唯一的直线

方程组（3）是我们上学的时候经常做的习题，在做作业的时候，只要未知数的个数和方程的个数相等，我们就可以把它给解出来。

这种方程的个数和未知数的个数相等的方程组，我们把它叫住正定方程组。它的特点是有唯一确定解（当然这是有前提条件的，比如图4中的两个点不能在同一个位置上）。

在测量的时候，我们是经常有意识或者无意识的在用正定方程组，比如建基准系的时候，所谓的“3-2-1”原则中的“3”，指的是第一基准建立的时候，要在一个平面上采3个点（3个点不在同一条直线上），就能确定一个唯一的平面。因为平面方程是

显然平面方程有3个未知的参数a,b,c，三坐标采了3个点，软件就能列出有3个方程的方程组，也就是正定方程组。然后解出出a ,b,c这三个参数，得到平面方程，然后就可以想干嘛就干嘛。

“2”用在第二基准的建立，要求在产品表面上采2个点。它也是一个正定方程组，因为除了过两个点（有了两个方程），还要加一个和第一基准的垂直约束（第三个方程），也能列出一个正定方程组。

“1”也是一样，过一个点，加上和第一基准，第二基准，两个垂直的约束，也是一个正定方程组。

站在设计工程师的角度来说，我个人是怀疑3-2-1原则的合理性的，这个原则可以使软件的计算变得简单，但是和实际装配的符合性不好。实际上，我们希望测量工程师在第一，第二，第三基准上的采的点越多越好，才和实际装配接近。

如此一来，我们就不得不面临一个苦逼的问题，超定方程组。

1.3 超定方程组

还是用直线举例，假如测量工程师在一个面上采了3个点P1(x1,y1)，P2(x2,y2), P1(x3,y3)要我们求出过这3个点的直线方程。根据我们前面套路，我们可以把这3个点分别带入直线方程（1），得到一下方程组：

这时，你凭直觉，是不是有一种不好的预感呢？未知数k和b可能没有解, 因为方程组（4）中很有可能两个方程之间的关系是矛盾的。大家可以想象一下，如果P1, P2, P3这3个点不在同一条直线上，如何去求过这3个点的直线呢？

图4 过三个点能确定一条唯一的直线？

显然，去寻找一条同时过这3个点的直线肯定是扯，因为它根本就不存在。也就是说，不存在一个k和b, 使得三个点都在同一条直线y=kx+b上。

所以方程组（4）的特点是，它的方程的个数大于未知数的个数，这样的方程组，我们把它叫住超定方程组。

超定方程组，听起来是不是很牛逼的样子？

事实上是苦逼，因为它没有解。

更苦逼的是，在我们现实的测量中（甚至公差分析中），面临的都是超定方程组。比如，在一个实际平面上采8个点（放心，这8个点一定不在同一个平面上），非要让你解出一个平面，你面临的就是一个解超定方程组的问题。

比如，前面讲的直线，变态的是，测量工程师可能采了12个点，需要软件算出一条直线，软件怎么办？

所以在测量的时候，需要解超定方程组简直就是家常便饭。

明明知道没有解，非要去解，那怎么办呢？没有办法，日子总得过下去，我们只能找出一个近似解来“将就”一下。

上帝并没有让我们完全绝望，超定方程组有个特点，那就是它有唯一的最小二乘解。

最小二乘解就是近似解的一种。最小二乘法的特点在本公众微信号的《来认识传说中的最小二乘法》中已经介绍过，有兴趣的小伙伴，可以点击文章最后的链接。

如何求得这个最小二乘解呢？它有固定的公式，这正是本篇文章的目的。在介绍最小二乘法的公式之前，我们还有个难题必须要克服，那就是要认识矩阵和矩阵相关的概念，我们马上进入第2节。

2. 矩阵的初步概念

说到矩阵，可能有一半的小伙伴被吓跑了。

矩阵本身是个非常好用的数学工具，大约是因为上学那会儿为了应付考试，没有看到它的真正用处，可能很多小伙伴和我一样开始对它有心理阴影了。

本篇文章尽量只简单介绍和最小二乘法数学公式相关的矩阵的3个概念，1. 矩阵的概念和矩阵的乘法，2. 矩阵的转置，3. 矩阵的逆矩阵。

2.1 矩阵概念和矩阵的乘法

矩阵，其实就是表格里的一堆数。我们上学那会儿，学的123，xyz等等都是单个数单个数来认识的，然后进行处理和运算。而矩阵，则是多个数，放在一起，很简单。

举个例子，共享单车的兴起，据说救活了很多濒临倒闭的自行车厂，因为他们收到了很多订单。比如下面是某自行车的两个分厂2018年供给各共享单车品牌的销售清单，单位万辆。

以上的这个自行车销售清单的表格，我们就可以用矩阵来表达, 给矩阵取个名字叫A，就有：

上图中用中括号表达的这个东西就是高大上的矩阵A, 它就包含了表1中的所有信息。它是不是就是一张表格？所以它就像表格一样，可以有很多行，也可以有很多列。

我们再来，因为每个品牌单车的样子和型号不一样，所以自行车单价也就不一样，下面是每个品牌单车的单价清单（单位RMB）。

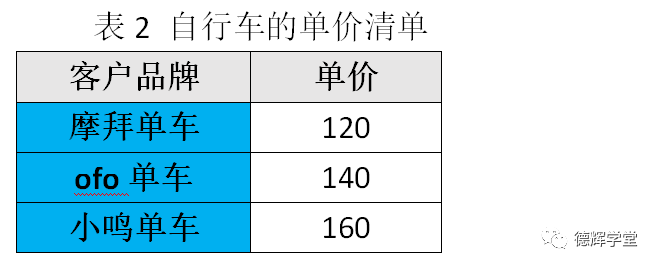
上面这个表格，也可以写成矩阵的形式, 给矩阵取个名字叫B. 则有：

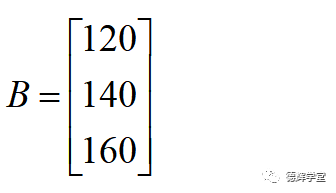
所以，矩阵其实就是把一堆数字，按特定顺序放在特定位置的一张表格里。

好了，我们对矩阵有了一个初步的认识，我们再来粗粗的认识一下矩阵的乘法。

继续我们的故事，到2018年年底，各品牌共享单车一分钱都没有给自行车厂家，流言传来，说共享单车不行了，这时自行车厂家慌了，赶紧核算一下各分厂这一年的损失。

这个算法小学生都会做的，我们把表格放在一起，很容算出来杭州分厂和上海分厂的损失（数量x单价=金额）。

图5 自行车厂家的损失

图3中第三张表格，显示的就是自行车厂家损失的计算方法，损失的结果也可以用矩阵C来表达，则有：

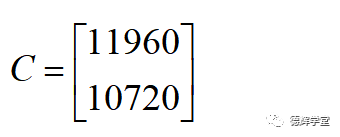
好了，从数学上讲，我们还可以用矩阵的乘法来表达上面的结果，很简单：

A∙B=C

即为：

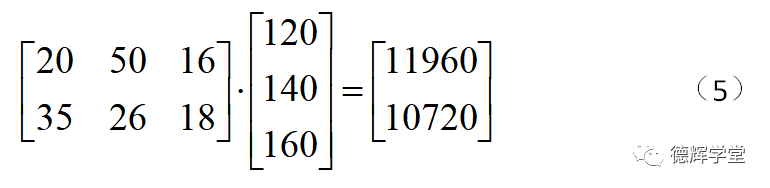
公式（5）就是矩阵的乘法，这个就像我们平时用的加减乘除一样，就是一种算法，通过矩阵的乘法，我们就可以直接计算出自行车厂家各分厂的损失。

大家最细要仔细观察等式（5）和图5中第三张表中的11960和10720是怎么来的。矩阵乘法，对初学者来说，稍微麻烦一点，要记住结果的规则，我列一个公式：

等式（5）的结果就是根据公式（6）计算出来的，公式（6）就是矩阵乘法的游戏规则。有兴趣的小伙伴最好记住，因为很多时候，我们需要根据方程组，也就是等式（6）的右边的样子，反推回等式左边的样子的。

大家注意到没有，矩阵的好处是可以“批处理”同类型的计算（当然，矩阵的好处远远不止这些）。

如果你实在记不住，也不愿意记，怎么办？没有关系，用Excel里的一个函数MMULT（）它可以直接帮你计算，你记住这个函数就好了。见图6：

图6 利用Excel的函数计算矩阵乘法

2.2 矩阵的转置

矩阵里有行，也有列，如果同行变成同列就是转置（相当于翻转）, 比如把第一行变成第一列，第二行变成第二列...。矩阵A的转置后叫转置矩阵，转置矩阵就记着：

举个例子吧，假设有：

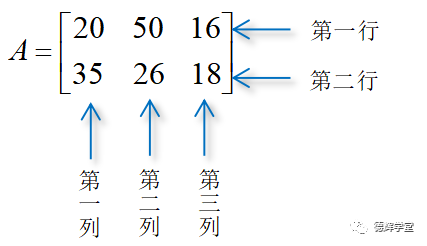
把A矩阵的第一行变成第一列，第二行变成第二列，就可以得到A的转置矩阵。那么矩阵A的转置矩阵为：

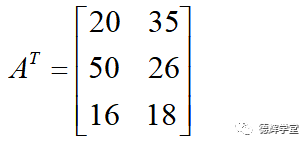
所谓转置是不是很easy?

还是怕弄错？好吧，没有关系，Excel里边有个函数Transpose()可以帮你完成矩阵的转置。

2.3 矩阵的逆

矩阵的逆，我们不深入了解，暂时把它想象成矩阵的倒数（其实矩阵没有这个倒数这个概念）。

任何一个非零数乘以它的倒数，结果是1，而这个1其实就是一个单位。所以有时候我们用乘以倒数的方法来代替除法。

矩阵里边也有类似1一样的单位矩阵，比如：

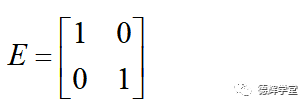
上面的矩阵E就是一个2阶的单位矩阵。所谓逆矩阵的特点，就是任何一个矩阵乘以它的逆矩阵等于单位矩阵。比如：

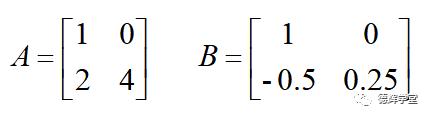
根据前面讲的矩阵的乘法规则，我们会发现：

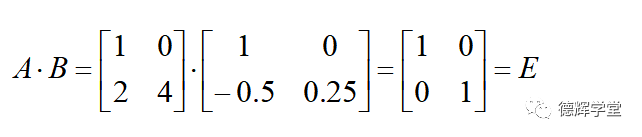
所以，B就是A的逆矩阵，A也是B的逆矩阵。记为：

这里要强调一下，只有方的矩阵（方阵），即行数等于列数的矩阵才有“逆”这一说，而且就算是方的矩阵，也不一定有逆矩阵（它的充要条件是行列式不等于0），类似不是任何数都有倒数的原理一样（比如0就没有倒数）。

问题是，如果我已经知道了一个矩阵，如何求它的逆矩阵呢？其实手工求比较麻烦，还要引入伴随矩阵之类的概念，不去深入了。我们还是偷懒，直接用Excel吧。

Excel里边有一个函数叫Minverse(), 它直接可以求出逆矩阵。如果逆矩阵不存在，他会提示出错。

3. 最小二乘法的公式和案例

好了，我们做了很多铺垫，讲了超定方程组，讲了矩阵和矩阵的乘法，转置矩阵，逆矩阵等概念，千呼万唤，现在终于可以把最小二乘法的公式给牵出来了。

定义 对于超定方程（矩阵方程）

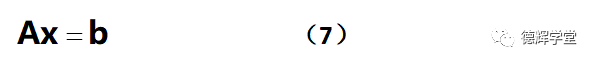
如果满足

可逆（这个条件大家不用担心，只要用三坐标采的点不再同一个位置上，肯定是可逆的），那么该超定方程（7）有唯一最小二乘解，且解的公式为：

这个公式（8）就是我们今天的主角。

需要说明的是，公式（7）中，A, X, b他们都是矩阵（所以它们被加粗），A和b是已知的系数或者值，x是不知道的未知数矩阵（如果你在这里开始懵圈不用急，后边我们还会举例来认识这个公式）。

公式（8）就是最小二乘法的解法，看起来很复杂的样子，但是对我们来讲，只要知道超定方程（7）中的系数矩阵A和b, 利用公式（8）就可以轻松解出最小二乘解x.

这个公式怎么来的？为什么成立？这解释起来太痛苦，必须要具备比较全面线性代数的知识，从基到张量空间再到坐标去解释，为了不让最后几个读者跑掉，不再讲了。

反正，有兴趣的小伙伴可以去查阅本文后边的文献。不过我可以把手按在手机上发誓，这公式不是我杜撰的，而且确定是正确的，算出来的这个x一定能满足平方和最小。

还要补充一下，公式（7）是一个矩阵方程，而我们前面讲的是线性的超定方程组，所以我们要学会自己把方程组转化成矩阵方程。举个例子，前面的超定方程组为：

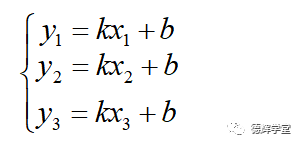
稍微做一个变化：

这样就可以转化成矩阵方程了：

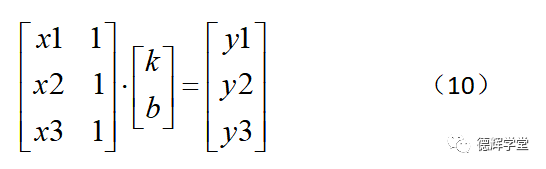
上面这个矩阵可能有点突然，如果大家把方程（10）中等号左边的矩阵乘法按照乘法的游戏规则（6）打开，就是方程组（9）了。

这一点还比较重要，有兴趣的小伙伴最好能熟练变换。

矩阵方程（10）中的x1,y1,x2,y2,x3,y3都是已知点的坐标数据，k和b是未知数。我们再给每个矩阵取个名字。令：

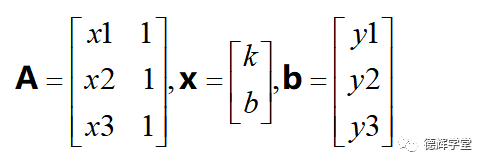
则矩阵方程（10）就可以写成：

看到没有，上面这个就是把超定方程组（9）转化成标准的矩阵方程了，它的好处在于我们可以直接套公式。所以，我们能再利用公式

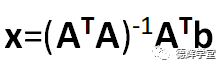
把k,b给解出来。

我就把它的长公式写出来吧。

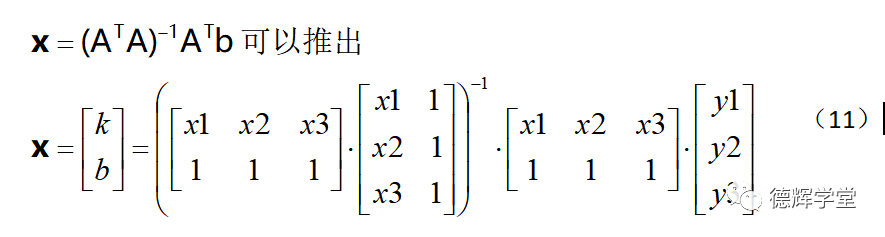
公式（11）看起来很复杂，其实右边那一堆就像加减乘除一样，最终得出一个2行1列的矩阵。如果你耐心把它输入Excel里边，也就是一步计算的事啊。

到了这里，k和b的最小二乘解就解出来了。

为了能够Excel来帮我们计算，我们再回忆一下Excel中的三个处理矩阵的函数：

如果你已经有了矩阵方程Ax=b, 也就是说你有已知矩阵A和b, 那么用Excel计算最小二乘解x就是分分钟的事情。你只要在Excel里边输入一个长长的公式就可以解决。当然你也可以一步一步输入公式计算。

数学公式为：

利用Excel的函数公式为：

x=MMULT(MMULT(MINVERSE(MMULT(TRANSPOSE(A),A)),TRANSPOSE(A)),b)

这个公式耐心看，吃透，它和数学公式是一模一样的。如果你还是不明白，那就拷贝黏贴吧。

好了，到这里，我们还是举一个实际的例子吧。我在平面上采了5个点，坐标如下图所示，请把这5个点拟合成最小二乘直线，并写出直线方程：

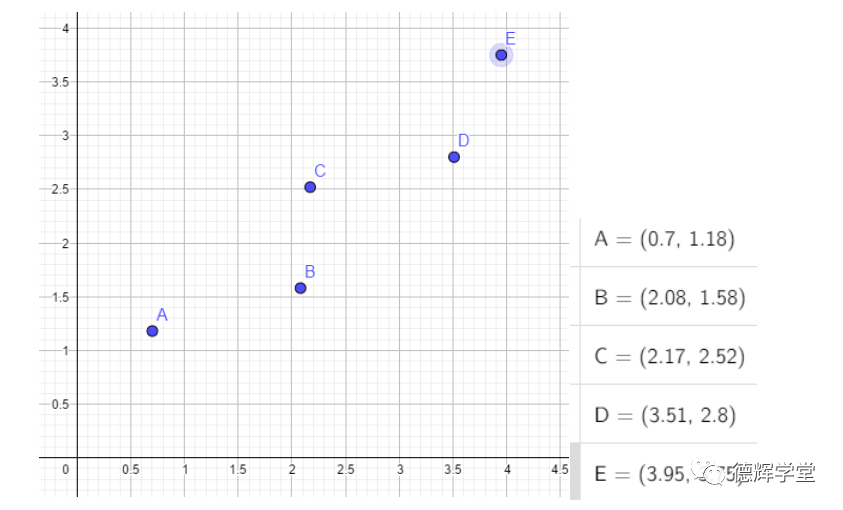
图7 5个点的分布

已知直线的方程为y=kx+b, 将A,B,C,D,E五个点带入直线方程，可以得到一个超定方程组（有些文献也把它叫做观测方程）：

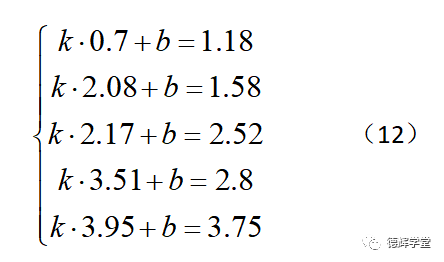
将超定方程组（12）整理成矩阵方程，如下：

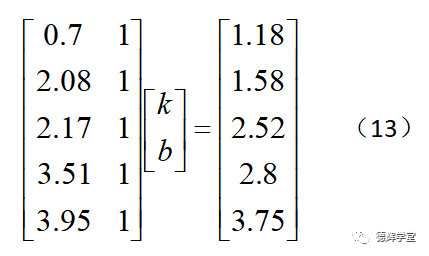
显然有：

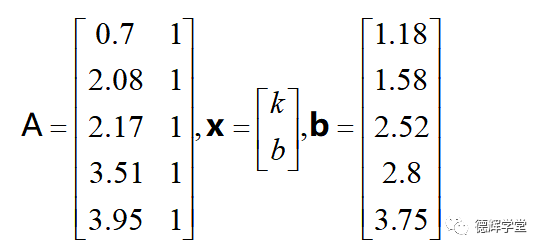
然后可以解得x的最小二乘解为：

所以可以得到直线方程的参数

k=0.731, b=0.551。

即最小二乘直线的方程为：

y=0.731x+0.551

Excel中的表格计算和公式输入，见图8：

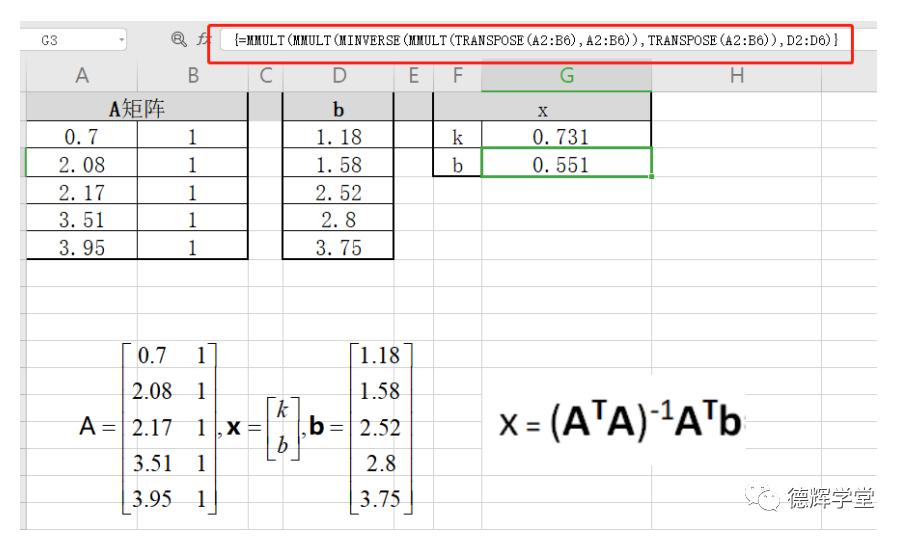
图8 Excel表格计算

我们再把最小二乘直线方程 y=0.731x+0.551和原来的5个点放在一起，做一下比较。见图9.

图9 最小二乘直线

显然，根据最小二乘法的规则，只有y这条直线满足残差的平方和e最小：

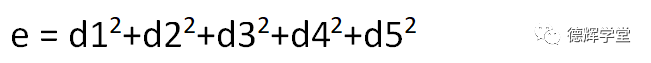
其中，也就是说，e值在所有可能的直线中，只有y=0.731x+0.551这条直线满足e是最小的。也就是说,尽管有点“将就”（也不得不将就），但是y=0.731x+0.551的直线已经是折衷后的优选方案了。

好了，最小二乘直线是拟合出来了，干嘛用呢？

该干嘛就干嘛，可以做基准去评价其它被测要素，可以做理想要素去夹被测要素（比如直线度），随你的便。

为了加深印象，我们再举一个例子，我们利用最小二乘法再来计算一个面轮廓度。

已知图纸标注和实际零件如图10所示：

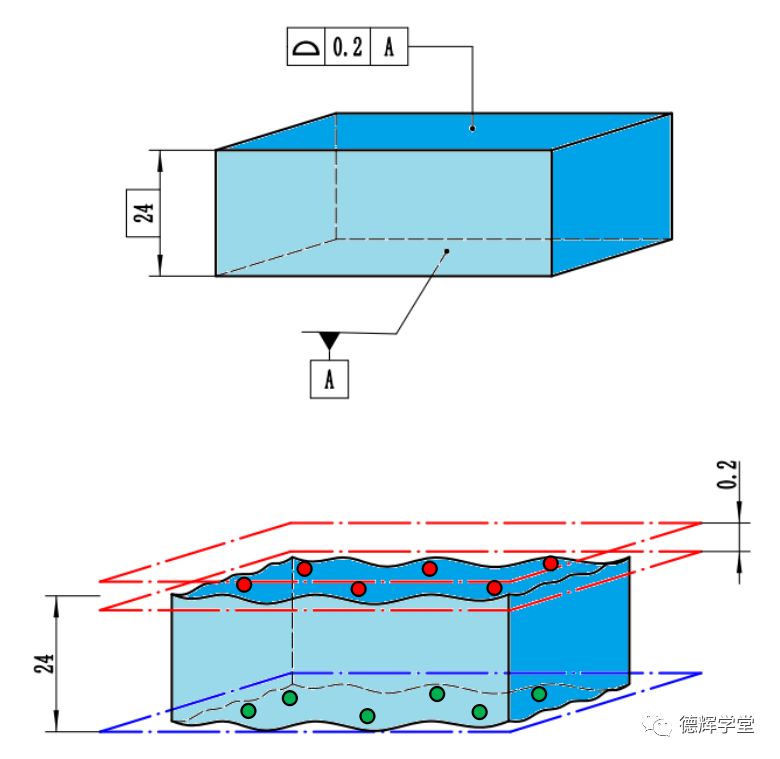
图10 图纸和零件上采的点

如图10，我们首先在基准要素（下表面）上采了六个点，点坐标如下：

被测要素（上表面）上采的点也有6个，数据如下：

因为平面方程可以写成下面的形式：

z=ax+by+c （14）

公式（14）中，a,b,c是平面方程的参数，只要知道a,b,c，我们就知道最小二乘法拟合出来的基准平面了。同样的方法，把D1，D2...D6的x,y,z坐标值分别代入平面方程（14），可以得到下面的超定方程组:

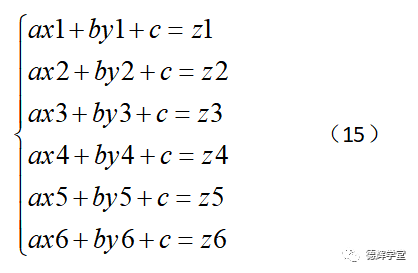
接下来的思路是如何把它转化成矩阵方程。我们令

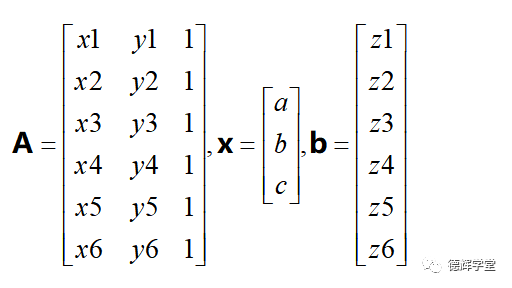
则方程组（14）就可以写成矩阵方程：

Ax=b

显然A是已知的系数矩阵（代入坐标值就已知），x包含3个未知数a,b,c， b也是一个数据已知的矩阵（所有的已知z）。我们就可以套公式啦。

我们将原始的数据整理成A和b, 然后利用Excel的函数：

x=MMULT(MMULT(MINVERSE(MMULT(TRANSPOSE(A),A)),TRANSPOSE(A)),b)

可以直接求出a,b,c。

Excel的具体数据如下：

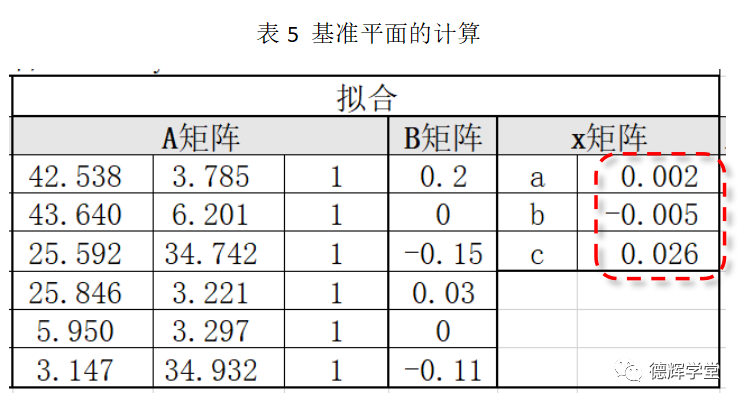
根据表5的计算，可以得到基准A的方程是：

为了方便后边直接套用公式，需要将上面这个基准平面的方程直接转化标准平面方程：Ax+By+Cz+D=0, 转化后为：

显然，标准平面方程，我们可以得出: A=0.002, B=-0.005,C=-1, D=0.026, 这四个标准平面方程的参数在算距离的时候，马上要用到的。

然后再求被测要素上每一个点到该基准面的距离，就可以算出轮廓度（根据ISO标准，轮廓度为和理论尺寸24差值最大的距离的2倍，）。这里需要利用点到面的距离公式（A,B,C,D四个参数刚好可以在这里用上）：

将被测要素每点的坐标代入公式（16），用点的实际坐标代替公式（16）中的x0,y0,z0。计算出每点到基准面的距离，最后可以计算出轮廓度（按照ISO标准）。最后的计算结果参考下面的表6。

表6 轮廓度的计算

根据上面的计算，可以得到轮廓度的实测值为0.344。

好了，我们的文章到这里快要结束了。

稍微回顾一下思路，我们求最小二乘解的时候，思路如下：

1. 写出目标函数，比如直线方程，平面方程；

2. 将已知点带入目标函数，构建超定方程组；

3. 再将超定方程组转化成矩阵方程Ax=b的形式（这一步有点难度，需要有兴趣的小伙伴们反复练习掌握）；

4. 利用公式

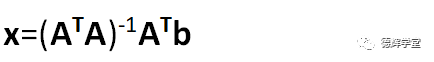
求出最小二乘解；

本期文章介绍的最小二乘解的公式，对线性问题适用（不仅仅是对测量GD&T, 其它地方也可以用），对非线性问题不能直接使用，如果要拟合最小二乘圆或圆柱之类的特征就没有办法直接采用这个公式。对于非线性的公式，如有机会，我们以后和大家讨论。

最后申明一下，本文的目的纯粹是为GD&T的发烧友们准备的技普知识，涉及到相关数学概念的解释一定有诸多不严谨之处，更加详细的，严谨的概念解释最好参考专业的文献，比如本文最后的参考文献。

本期小结

本期文章介绍了通过矩阵来计算最小二乘法的一个公式（注意，这并非最小二乘解的唯一方法），它非常简洁，但要求读者对线性代数有一定基础。为了照顾到把线性代数已经还给老师的小伙伴们，我们前期做了铺垫。第1节，讲了三种方程组，说明我们在拟合的时候，面临最多的是超定方程组。第2节，讲了矩阵的一些相关知识，为了帮助小伙伴们理解公式的含义。第3节才正式介绍最小二乘法的公式和相关例子，并用轮廓度计算作为例子，来解释了这个公式。

【后记】

写本期文章的过程非常痛苦，一方面在抖音，快手等超短，超爽视频流行的年代，公众号长文注定不受欢迎，而且还是针对专业化的小众文章；另外一方面，技普文章一旦遇到数学问题，马上就变得诚惶诚恐，因为数学既严谨，水又很深，一不小心就发现自己在肤浅的胡说八道。不管怎样，终于写完，不为别的，只为真正有好奇心的同行，哪怕寥寥无几。

这里要感谢OGP的伊扬威老师，他帮我用OGP的软件验证最小二乘法的计算结果的正确性，还热心的通过视频教我如何使用这款软件，让我有信心把这篇文章发出来。

如果你有任何问题，或者发现本文的错误之处，欢迎留言给我们。我也给你留一个思考题，在本文最后一个案例中，如果要求被测面相对于基准面A面的平行度，你可以通过今天的讲的公式计算出来吗？你可以留言告诉我们哦。

参考文献