在我们常用的测量软件里，比如说PC-DMIS, 我们经常会用到“T”值，如下图所示。

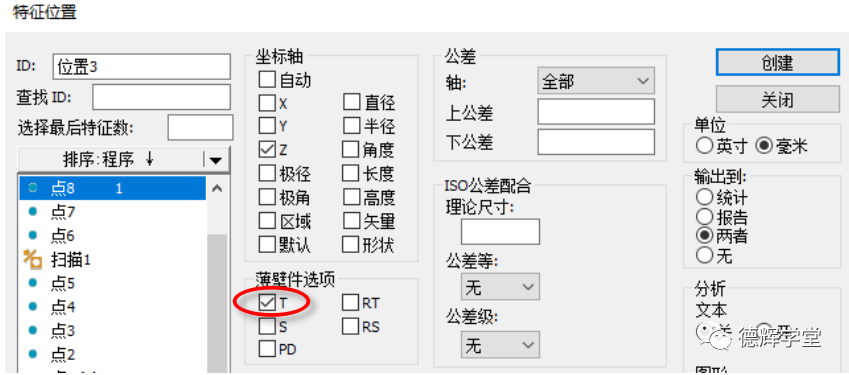
图1  T值

或者在测量轮廓度的时候，我们有时候难免会好奇，这个T值或轮廓度是怎么算出来的？它的计算原理或者公式是什么样的？

本期文章我们就来讨论一下这个话题。本期文章将分3个小节来讲解:

1. 一些基本的数学知识

2. T值的计算原理

3. 带基准轮廓度的计算原理

本期的话题有点难度，只针对对计算原理感兴趣的发烧友工程师们。如果对空间解析几何有概念的小伙伴，看起来会比较容易，对于不太了解空间解析几何但是好奇心强的小伙伴们，也没有关系，本篇文章在开头会做一些相关的基本数学知识介绍。

因为篇幅很长，本期文章分两次放送，今天这一次主要讲解第一小节，一些基本的数学知识。

1. 一些基本的数学知识

为了让各位在读的小伙伴彻底理解T值和轮廓度的计算原理，相关的数学知识一定是绕不开的。所以一开始，我们就来普及一下相关的数学知识。

三坐标计算的数学原理，基本上都来自于线性代数和空间解析几何。

上学那会儿为了怕挂科，考试前几天，天天熬夜啃课本的场景是不是还历历在目？那时心里特别憎恨数学这种破玩意儿，不知道像高数这种东西会用在哪里，而且心想那些所谓的数学家们心里得有多无聊才会发现那么多所谓的定理和公式？

当然啦，你知道的，参加工作后，才明白当时恨错了对象。

废话少说，回到主题，现在我们翻出当年的课本，抖抖灰。先回忆一下和本篇文章相关的3个基本的数学知识点。

1）矢量和矢量的加法

大家都听说过矢量，就是有大小，有方向的量就是矢量，也叫做向量。高中时我们学过典型的矢量就是力，速度之类的。

最早提出这个概念的，应该是亚里士多德。

当然，提起矢量，还有一个就是标量，只有大小没有方向的量，比如我们的工资，体重，颜值什么的。这里不再赘述。

矢量的加法，最常见的就是求力的合力，比如说我们已知两个力，一个是力a,一个是力b，如下图所示，如何求他们的合力c呢？

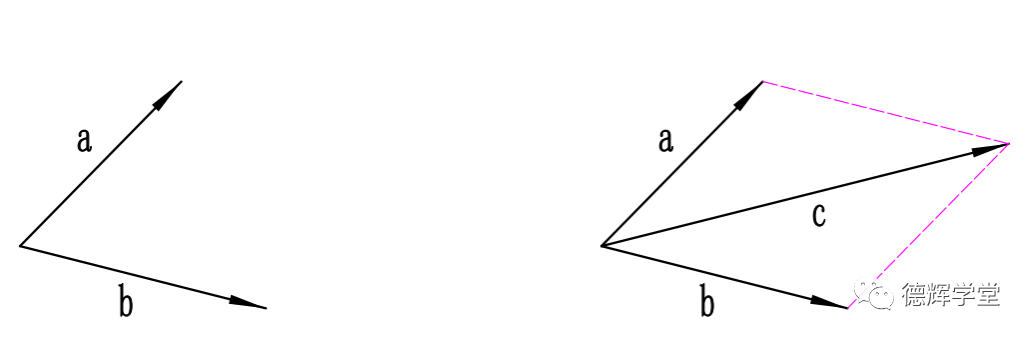
图2 平行四边形法求合力

我们常用的方法是平行四边形法，如图2中平行四边形的对角线c就是a和b的合力。我们把它记作：

c = a + b                          （1）

注意，公式（1）表达的是矢量和，而非简单的数值相加，所以c的大小的具体计算方法并非是把a的大小和b的大小直接相加，而是必须把a,b两个矢量投影到c上，再相加，相加的结果才是c的大小。

计算合力，其实更实用的方法，是采用三角形法。

图3 三角形法求合力

图3中就是通过平移个矢量，采用三角形法求合力。计算合力c的公式也是c = a + b。本质上，三角形法和平行四边形法是一样的。

观察图3，可以看出，矢量a和矢量b箭头首尾相连，而合力c起始点就是a的起始点，c的终止点就是b的终止点（这也是尺寸链计算的数学基础）。

所以基于图3，假设已知矢量c, 和矢量a, 如果求矢量b的话，不难求出：

b = c - a                         （2）

公式（2）就是矢量的减法。

到这里为止，我们只是介绍了矢量最简单也最朴素的基本知识点，要解决三坐标的算法问题，它还不够，我们继续往下走。

2）矢量坐标和矢量坐标的加法

在三坐标算法里，我们常常更喜欢用坐标来表达矢量，它更加方便计算。

假设在3D坐标系中有一个点A（见图4），它的坐标是(x1, y1, z1)，那么从坐标原点O指向该点A就可以看成一个矢量，记作OA, 该矢量OA的坐标就是(x1, y1, z1)，记作：

OA = (x1, y1, z1) = x1i + y1j + z1k

     其中，i, j, k分别表示x,y,z轴正方向的单位向量。见图4。

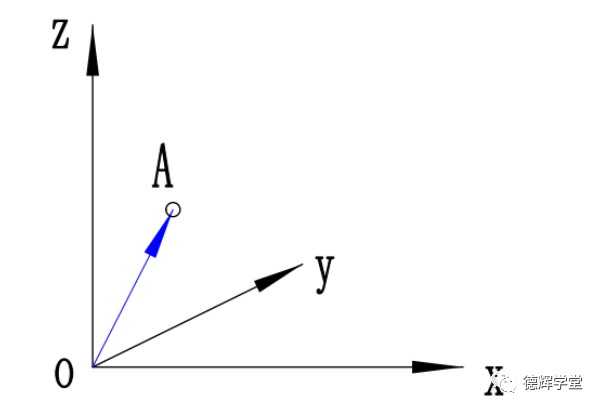
图4 矢量坐标

注意，同样都是坐标（x1, y1, z1）, 作为点坐标和作为矢量坐标是完全不同的两个概念，作为点坐标只是表达该点在坐标系中的具体位置；但是如果表达的是矢量坐标，它提供了两个信息：

1. 该矢量的方向，由O指向A，我们甚至可以计算出OA和每个坐标轴的夹角。

     2. 该矢量的大小。即OA的长度，专业术语称为OA的模，记作lOAl. 且有：

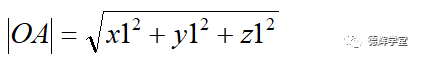
注意，这个模的计算公式，我们后边会频繁用到，请各位小伙伴把它记住。

假设我们已知另外一个点B的坐标是（x2, y2, z2）。那么OB的矢量坐标则为（x2, y2, z2），假设矢量OC为OA和OB的矢量和，即 OC= OA + OB根据矢量的加法原理，则有：

OC = OA+OB 

      =（x1i + y1j + z1k）+ （x2i + y2j + z2k）

      =（x1+x2)i+(y1+y2)j+(z1+z2)k  

      = (x1+x2, y1+y2, z1+z2)                  （2）

具体见图5. 

其中C点的坐标就是(x1+x2, y1+y2, z1+z2)。

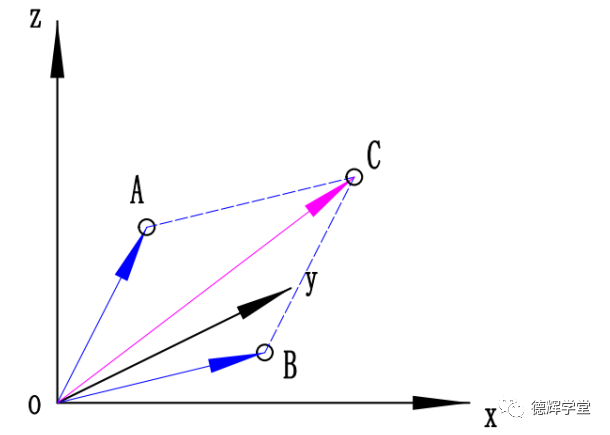
图5 矢量坐标相加

在实际的工程应用中，我们可能会更加关心线段AB的相关特点，比如图5中线段AB的长度是多少？它在空间中的姿态（和x,y,z轴的夹角）是怎样的？

所以我们更常用的是矢量的减法。

     如果我们将点A和点B连起来，形成一个线段AB，而且将A指向B的方向作为该线段的方向，此时，我们就得到一个矢量AB, 见图6：

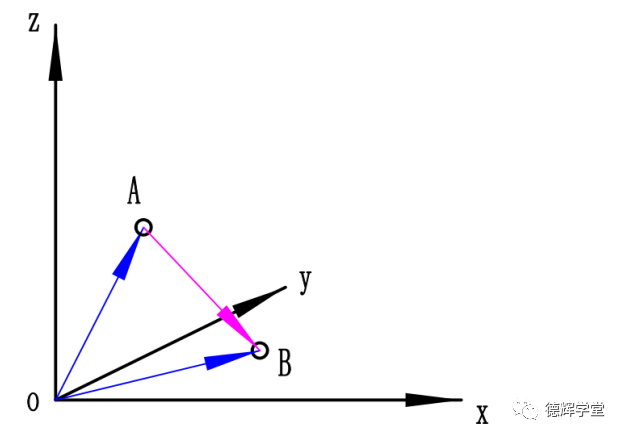
图6 矢量坐标相减

仔细观察图6中箭头的特点，因为向量OA和向量AB的箭头首尾相连形成OB，所以有：

OB = OA + AB

转化后可以得出：AB = OB - OA

又因为OA的矢量坐标为（x1, y1, z1），OB的矢量坐标为（x2, y2, z2），根据矢量的减法原理不难得出：

AB = OB - OA

      = （x2i + y2j + z2k）-（x1i + y1j + z1k）

      = （x2 - x1）i +（y2 - y1）j +（ z2 - z1）k

      = （x2-x1, y2-y1, z2-z1）                  （3）

注意，公式（3）非常实用，我们可以利用公式（3）计算关于AB的两个信息：

     第一个是AB的长度：

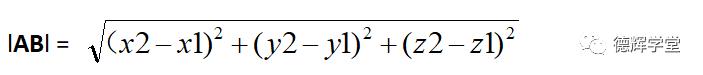
这个公式是不是和3D空间中已知两个点A,B的坐标，然后求AB之间的距离的计算公式是一样的？没错，所谓条条大路通罗马，用向量也完全可以计算出两点距离！

第二个是向量AB和x,y,z轴的夹角：

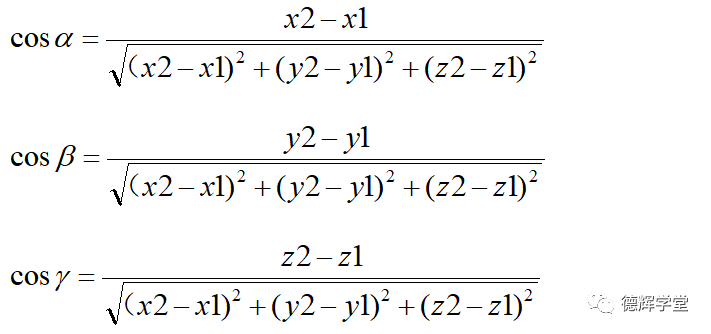
其中，

分别表示向量AB和三个坐标轴xyz形成的夹角。本文暂时用不上上面3个看起来高逼格的余弦公式，开始头疼的小伙伴可以直接略过。

可能有很多小伙伴想不通, 那个坐标（x2-x1, y2-y1, z2-z1）究竟在坐标系的哪个位置？我们将图6中的矢量AB在坐标系里平移，让A点和坐标系原点重叠，我们将得到一个新的矢量OD，见图7。

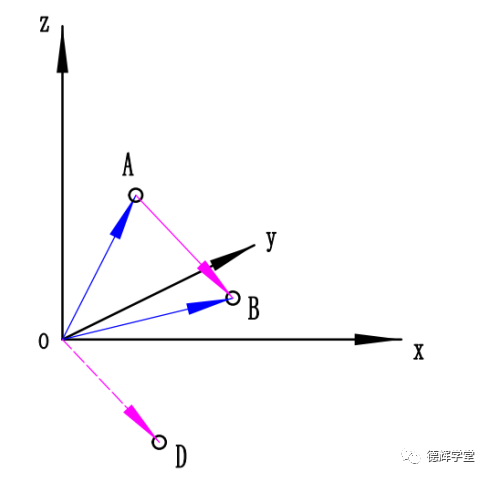
图7 相减后的矢量坐标

注意，图7中的D点的坐标就是（x2-x1, y2-y1, z2-z1）！

我们知道矢量OD是通过平移矢量AB得到的，它们两个有区别吗？

答案是，没有区别！因为对于直角坐标系中的矢量来说，人们并不关心它在空间中的具体位置，只关心它的方向和长度，基于这个特点，在图7中，我们可以得到这个结论：

AB = OD

稍微回顾一下。

到这里我们已经扯了好多。不想知道推导过程，只想知道结论的小伙伴，可以记住本小节的结论：

在已知两个矢量OA（x1, y1, z1）, OB（x2, y2, z2）的矢量坐标的前提下，如果要计算他们的加减法，很简单：

1. 要计算OA,OB的加法: 相应的坐标直接相加即可。

OA+OB=（x1+x2, y1+y2, z1+z2 ）

2. 要计算矢量AB的矢量坐标，直接采用减法。

AB=OB-OA=（x2-x1, y2-y1, z2-z1 ）

本篇文章中，主要用减法。

注意，上面的减法的坐标不要弄反了，如果是AB（A指向B）的坐标向量，是后边B点的坐标减去前边A点相应的坐标。如果是BA（B指向A)，则需要反过来。

我们再往下走。

3）矢量和矢量坐标的乘法（数量积）

我们接下来再探讨一个和本文内容相关的第3个数学知识点，那就是矢量的乘法。

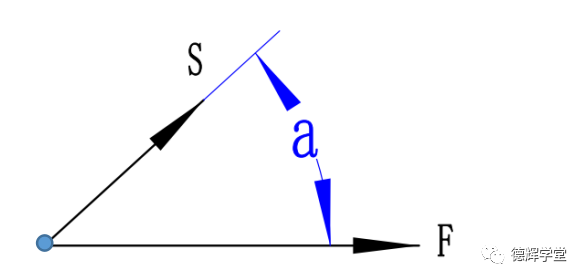
图8 力和位移

如图8所示，已知一个物体在力F的作用下产生了位移S，那么请问力F做的功是多少呢？显然根据我们上学所学的物理知识，不难得出：

W=lFl*lSl*cos(a)

在解析几何里边，力F所做的功也可以用向量来表达：

W=F∙S

注意，向量F和向量S的这种乘积关系，专业术语称为数量积或者点积，中间有个点表示乘，而不能用乘号“x”表示，如果用“x”, 那是另外一个概念，叫向量积。

本篇文章我们只讨论数量积（点积）。

所以由上面两个公式，我们可以得出：

W=F∙S=lFl*lSl*cos(a)                        （4）

可以看出，两个有方向的矢量的数量积或点积的计算结果是一个没有方向的标量，比如上面的功W。

同样，已知矢量OB和矢量OA的矢量坐标，如何计算它们的数量积呢？见图9，其实，计算他们的数量积并不困难。

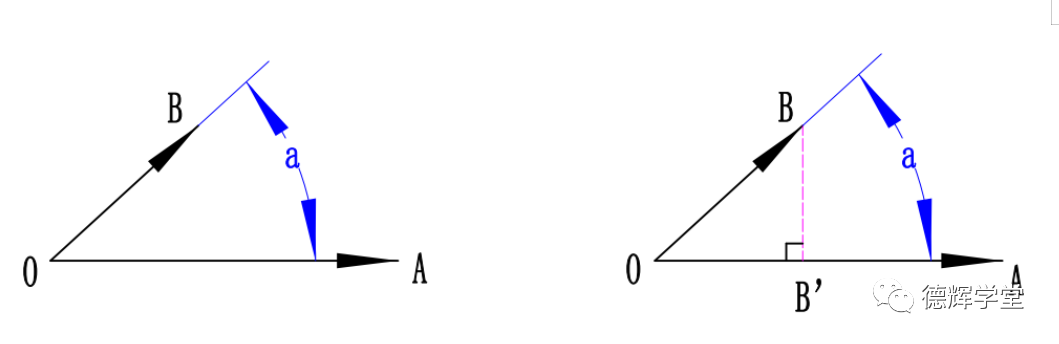
图9 两个矢量的数量积

根据公式（4），我们可以得出：

OB∙OA=lOBl*lOAl*cos(a)                  （5）

此时，我们再做进一步研究，过B点向OA做垂线，垂足是B’, 这时，lOB’l我们称它是矢量OB在矢量OA上的一个投影。

注意，这个OB’有非常重要的研究价值。再一次强调，lOB’l就是OB在OA上的投影。

投影是一个非常非常重要的概念，需要要引起重视，因为后边我们讨论的T值，就是某个向量在另外一个单位矢量上的投影！而轮廓度我们计算的也就是T值，它也是投影！

我们后边搞来搞去，就在求这个投影。

如何求得投影的长度呢？不急，我们慢慢来。

尽管投影非常重要，计算它的长度却非常简单。见图9中右图，根据三角函数关系，不难得出投影OB’的长度：

lOB’l=lOBl*cos(a)                      （6）

所以把公式（5）和公式（6）整合一下：

OB∙OA=lOBl*lOAl*cos(a)

           = lOB’l*lOAl                    （7）

公式（7）说明，两个向量的数量积，就是一个向量的投影的模乘以另外一个向量的模。

我们再往下走，各位请耐心跟下去。

已知矢量OA的矢量坐标是（x1, y1, z1），OB的矢量坐标是（x2, y2, z2），我们也可这样表达:

OA = x1i + y1j + z1k    OB = x2i + y2j + z2k

那么OB和OA的数量积可以表达为下式：

OB∙OA =（x1i+y1j+z1k）*（x2i+y2j+z2k）

             = x1*x2+y1*y2+z1*z2            （8）

公式（8）是不是来得太突然？如果我们耐心的把公式（8）慢慢展开, 再结合下面公式：

i∙i = j∙j = k∙k =1,     i∙j = j∙k = i∙k = 0

所以不难得出公式（8）的结论。为了不把各位小伙伴搅晕，这里不再详细展开。

不管怎样，已知两个矢量的矢量坐标，那么该两个矢量的数量积，就是他们对应的坐标乘积之和。

再说一遍，两个矢量的数量积就是他们对应的坐标乘积之和。这个就像最基本的加减法一样，我们要记住。

再结合公式（8）和公式（7），我们来推出终极公式：

OB∙OA=lOB’l*lOAl=x1*x2+y1*y2+z1*z2

稍做整理，可以推出：

lOB’l=（x1*x2+y1*y2+z1*z2）/lOAl  （9）

公式（9）就是我在这里啰里啰唆半天，想要得出的这个终极公式，它表示向量OB在向量OA上的投影长度的计算方法。这种计算方法在计算T值时会用到。

文章先到这里。我们下次再介绍这些公式在计算T值和轮廓度几何误差中的具体应用。

第一节小结

本小节有点装逼的学术味道，没有办法，在数学面前不得不严肃一回，吊儿郎当没法唬弄过去。

一开始做了很多基本概念上的解释，比如矢量，模，矢量及矢量坐标的加法，减法，数量积之类的概念。但是和T值及轮廓度相关的知识点无外乎两条。

1. 矢量的减法计算：已知空间坐标中的两点, 点A（x1, y1, z1）和点B（x2, y2, z2），利用矢量的减法，则可以得出矢量AB的坐标为（x2-x1, y2-y1, z2-z1 ），利用这个信息，我们可以得出AB的长度和方向角。

2. 投影长度的计算：已知空间坐标中的两点, 点A（x1, y1, z1）和点B（x2, y2, z2），利用矢量的乘法再整理，则可以计算出矢量OB在OA上的投影l OB’l 。投影计算公式为：

lOB’l =（x1*x2 + y1*y2 + z1*z2）/lOAl 

看完本期文章后，觉得本期文章对您有用吗？还是有卵用？或者您有其他不同的观点，欢迎给我们留言！