在本期文章开始之前,我们先回顾一下上一期文章的内容。
上期我们讨论了平移,旋转和敏感度(Sensitivity),平移的敏感度始终为1,和结构无关。而旋转的敏感度和结构有关系, 比较可怕的是它可能会大于1。基于这个理论,我们讨论了敏感度对测量的影响(严格意义上讲,是对加工工艺的影响),一句话,我们害怕旋转的原因是,在旋转运动中,结果变量O和原因变量C之间的关系不是1:1, 还有一个以敏感度作为放大系数的参数在作祟。
那么敏感度又和谁相关呢?显然,敏感度和产品结构相关(和原因变量点与结果变量点到旋转中心的距离有关),这就给了结构设计工程师,或者尺寸工程师很大的灵活度,可以通过改变结构来优化设计。
我们现在知道了旋转和敏感度的特点,它对我们的实际设计和生产有什么指导意义呢?
作为设计工程师,或尺寸工程师,如何利用旋转的特点,来改变敏感度,从而优化我们的设计呢?
本期,我们就来讨论一下和设计相关的话题,本期文章将完成上期剩下的两个章节:
3.旋转对设计的影响
4.旋转与稳健性设计
3. 旋转对设计的影响
我们以汽车的后背门和灯带之间的装配为案例,来分析旋转带来的影响。本章节又分两个小节,首先分析旋转对设计带来的影响,然后我们再讨论解决办法。
3.1 旋转对设计带来的影响
图1是汽车上后背门和灯带的装配总成,我们先来了解后背门和灯带之间的装配关系。
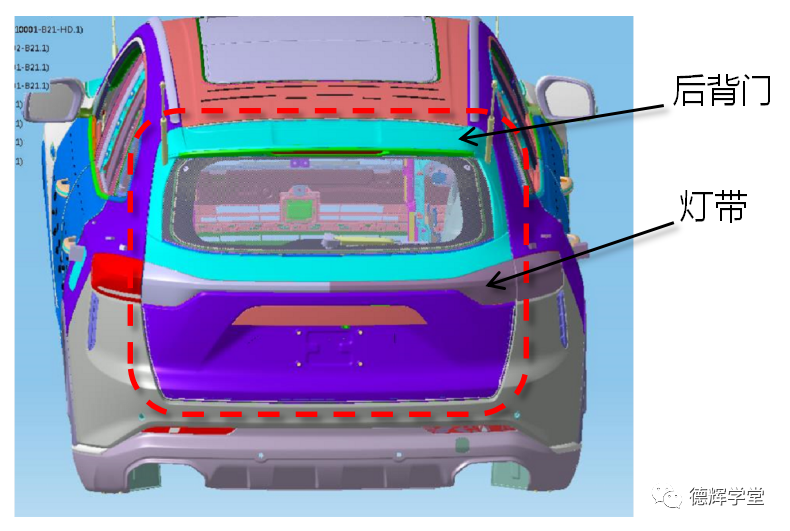
图1 后背门总成图

图2 灯带
图1和图2分别显示了某款车型的后背门总成和灯带,根据汽车行业的要求,对后背门和灯带之间的缝隙有DTS(尺寸技术规范)要求,见图3。
比如缝隙大小Gap=3±1,缝隙均匀度(即最大缝隙和最小缝隙之差)小于1.2之类的。
(因为本期文章我们只做定性分析,不做定量分析,所以缝隙大小和均匀度的具体要求不是我们的重点。)
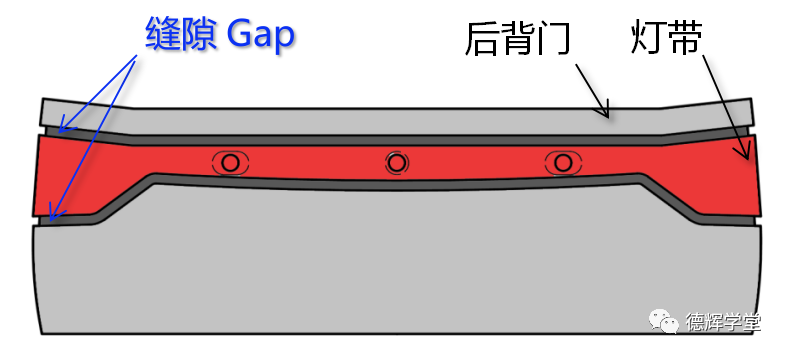
图3 灯带缝隙DTS要求
我们的目标就是分析有哪些因素在影响图3中的缝隙(Gap)。
分析公差的第一步就是分析产品的装配关系,也就是定位关系。如果我们单独把灯带和后背门拆开,发现它们之间的定位关系非常简单,典型的一面两销定位,哦,不对,是一面三销定位。
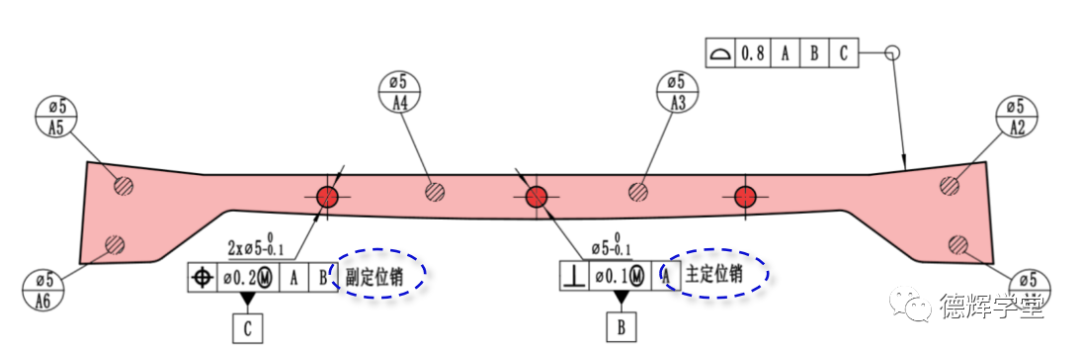
A. 灯带简图
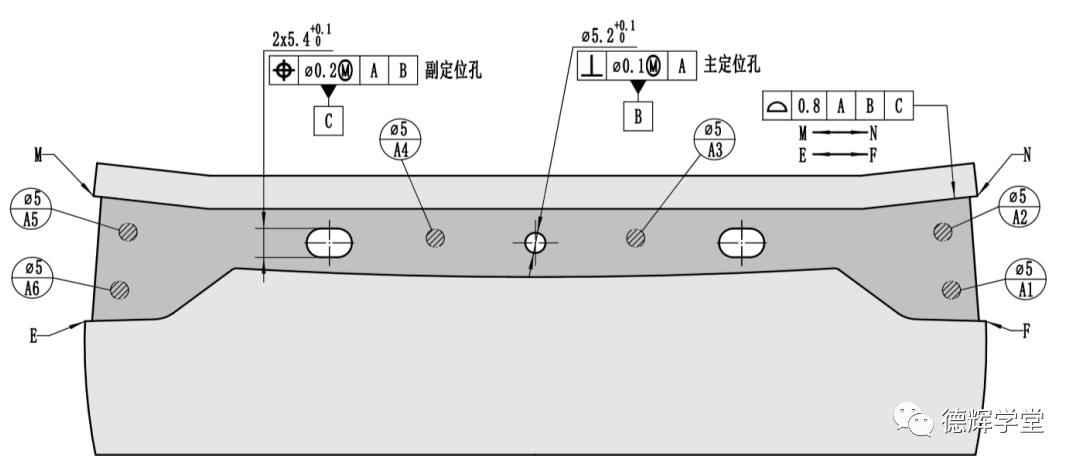
B. 后背门局部简图
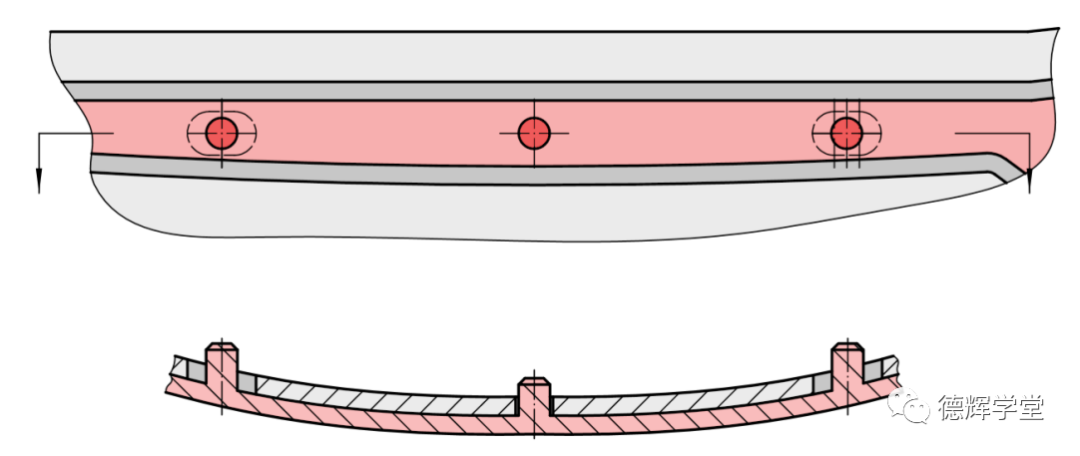
C. 一面三销定位细节
图4. 后背门,灯带简图及定位细节
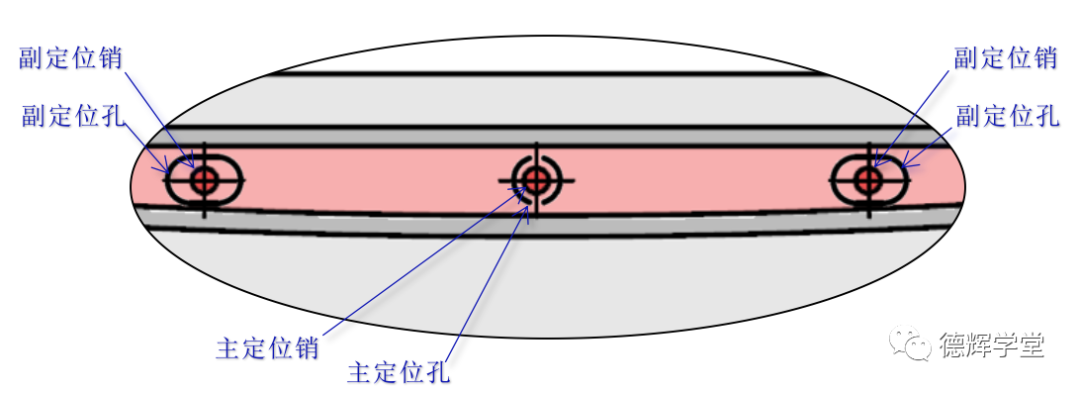
如图4A中所示,红色灯带除了安装面(A1-A6)以外,有一个居中的主定位销,和两个分布在两侧的副定位销,见图4A中的蓝圈部分。
与灯带装配的后背门对应的定位特征,是一个圆孔(主定位孔)和两个长腰孔(副定位孔),见图4B。
我们假设后背门不动(即以后背门为参考系),那么灯带在后背门上有六个自由度,它们是被上面说的这些定位特征限定的。
显然,主安装面约束3个自由度(哪3个自由度,小伙伴们自己想), 主定位销约束两个平移(基于车身坐标系,就是Y方向和Z方向的平移,即Ty和Tz), 而两个副定位销则约束围绕X轴的旋转, 即Rx。见图5。
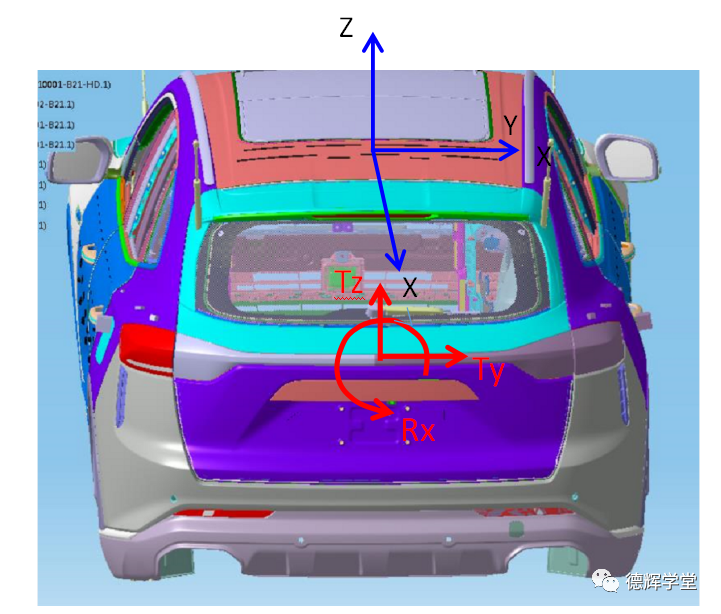
图5 车身坐标系及自由度
为了让大家直观的理解定位特征对灯带自由度的约束,还是来看看动画吧。

动画1 主定位销约束Ty和Tz平移的自由度

动画2 副定位销约束旋转自由度Rx
动画1显示了主定位特征约束灯带平移的自由度,动画2显示了两个副定位特征约束灯带旋转的自由度。
这里多一句嘴,很多小伙伴一看到有两个长腰孔,马上感觉不舒服,在旋转方向上,这不是过定位吗?
过定位又怎么了?
我们为什么对“过定位”有如此大的心里阴影呢?常见的直观经验是,装配时,这些过定位的特征容易被“卡”住(在定位功能上互掐),所以很多工程师一看到过定位的结构就马上啊啊的叫起来。事实上,过定位不会有害处的,如果我们能做到:
1.对于刚性零件,如果定位特征公差配置的合理(比如满足孔IB大于轴OB),看起来过定位,事实上干涉或卡住的现象永远不会发生。
2.对于非刚性零件,本身就是软的,能够容纳一定量的干涉,只要我们控制得当,在一定范围内(注意,是在一定范围内),过定位就过定位呗,又怎样?
但是过定位的好处也是明显的:
1.分散定位权力,定位特征之间相互制衡(这在政治上,这是多高的权术啊),可靠性好。
2.因为过定位,当零件产生微变形后,会有多点同时接触的现象,这样产品受力条件会比较好(比单点接触好),整体变形少。
基于上面的分析,你还是很讨厌过定位吗?
实在忍不住,又扯远了。
在了解了灯带和后背门之间的装配关系后,我们还是回来研究车身缝隙的话题。
搞公差分析的小伙伴都知道,分析灯带和后背门之间的缝隙误差的时候,我们必须要弄清楚误差源,即误差来源。
就本案例的缝隙而言,显然误差源有以下4类:
1. 零件自身的轮廓度误差(制造误差)
2. 孔销浮动
3. 装配变形
4. 其他误差
本期的话题,我们主要研究上面第2条误差源,孔销浮动给缝隙(Gap)带来的误差。
也就是说,在分析之前,我们做了一些假设,零件自身轮廓度满足要求,没有装配变形和其他误差。
什么是孔销浮动?(也有的文献叫装配偏移,Assembly Shift)
就是当实际孔比实际轴大的时候,孔轴之间有间隙了,所以孔轴之间有相对运动的的可能性。对于主定位销孔和副定位销孔之间,如果有了间隙,那么灯带相对后背门就会相对浮动(Shift)。孔销之间的间隙,具体见图6中的A图和B图。

A. 灯带和后背门的定位关系
A. 局部放大图
图6 孔销之间存在间隙
图6中的主定位孔销和副定位孔销之间,任意一个存在间隙(这种机率一定会发生),这些间隙就使所谓的“定位”功能丧失一部分。
设想一下,如果灯带和后背门的定位特征之间没有间隙存在,那么灯带相对于后背门的位置是固定的,因为没有任何自由度存在。
现在两零件的定位特征之间有了间隙存在,那么对自由度就有了“纵容”,这个纵容的后果就是,灯带相对于后背门有一定“自由度”的浮动。见动画3:
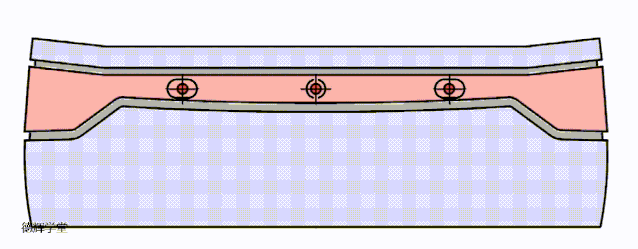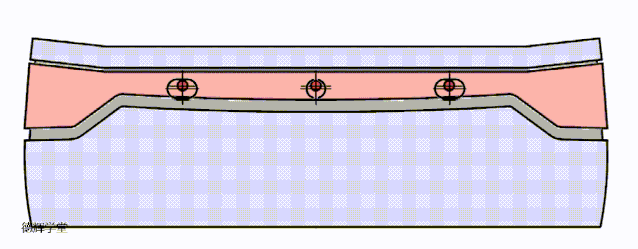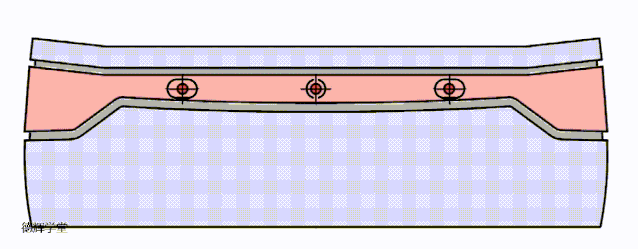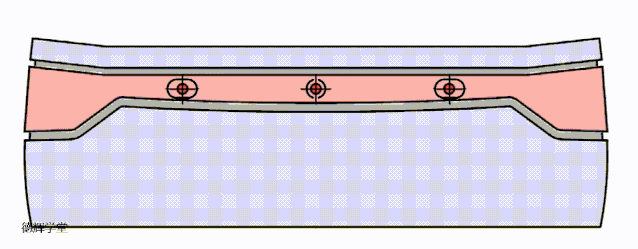
动画3 灯带的“自由度”
比较动画1,动画2和动画3, 不难得出规律:定位特征约束灯带哪些自由度,当孔销浮动产生的时候,定位特征就对灯带的这些自由度进行一定量的“放纵”(备注:这个和基准偏移,Datum Shift, 是一个原理)。
比如,主定位孔销之间的间隙,会使得灯带相对于后背门有一定量“平移”的自由度,而副定位孔销之间的间隙,会使得灯带相对于后背门有一定量“旋转”的自由度。
当然,如果主副定位销孔都有间隙存在,那么雪上加霜,后果就是灯带相对后背门的运动是“平移”和“旋转”的叠加。
孔销间隙存在,就必然存在孔销浮动,存在“纵容”,这种纵容一旦发生,会给我们产品带来额外的坏影响。比如说灯带和后背门之间如果存在孔销浮动,浮动是随机的,会影响缝隙。当灯带和后背门之间的固定螺钉被打紧后,实际的缝隙相对理论缝隙而言,会变得更大或更小,缝隙的均匀度会变得更加糟糕。
因为孔销浮动引起的“放纵”,对灯带和后背门之间的缝隙带来的负面影响,正是本期文章探讨的主题。
和上一篇文章一样,我们还是将问题分解开来,一步一步分析。
我们先建立一个简单的数学模型,见图7。
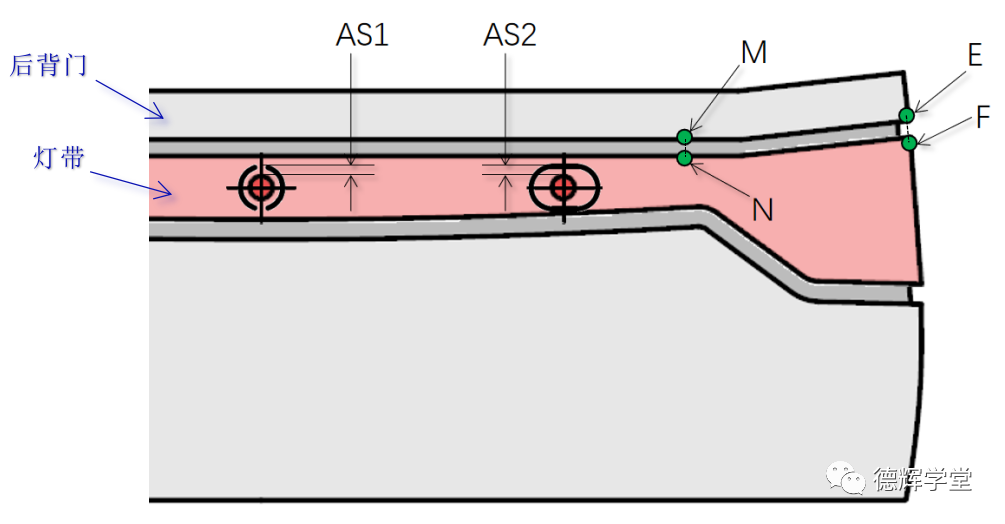
图7 灯带和后背门初始的相对位置
如图7示,我们在后背门上取两点,M和E点,在灯带对应的位置取N和F点,显然,MN的距离和EF的距离体现的就是后背门和灯带的缝隙大小(当然分析的话,点数是越多越准确)。
图7中的AS1表示主定位孔销之间的单边间隙,AS2表示副定位孔销之间的单边间隙,显然有:

我们的目的就是分析AS1和AS2对MN处的缝隙Gap1, EF处的缝隙Gap2
带来的影响。注意,上述公式仅仅用来计算最大的AS1和AS2,不需要考虑定位特征的几何公差。
先分析主定位孔销浮动带来的影响。
我们先假设副定位孔销之间的间隙为0,此时,如果主定位孔销之间存在间隙,那么孔销浮动会使得灯带相对后背门左右平移(长腰孔的原因)。
如果副定位孔销之间的间隙不为0(先不考虑旋转),那么在主定位孔销之间存在间隙的前提下,灯带相对于后背门不仅可以左右平移,还可以上下平移。见动画4。

动画4 主定位孔销浮动带来仅平移
我们把动画4中的孔销浮动的量夸张一点,让灯带使劲往下移AS1,即主定位销由原来的B点,移到B’点, 那么相应的, 灯带上的N点,F点分别移动到N’点,F’点。
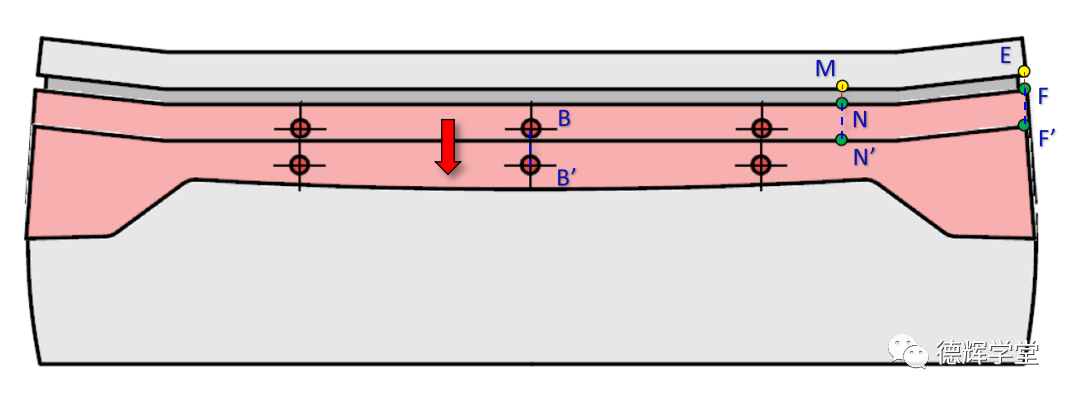
图8 主定位特征的孔销浮动带来的平移
图8中,BB’为原因变量,NN’和FF’为结果变量,又因为我们一开始总结的,平移的敏感度为1(即Sensitivity=1),不会减小也不会放大,显然有:
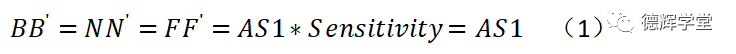
注意,上式中,BB’,NN’,FF’,AS1的数值,可能是正,也可能是负,取决于孔销浮动的方向。
也就是说,孔销浮动引起灯带位置的变动量NN’和FF’,可能使缝隙Gap变大,也可能使缝隙变小。
我们再回到后背门总成,对于灯带和后背门之间的缝隙,显然,孔销浮动AS1对缝隙MN和EF的影响是一样的。
MN处缝隙Gap1的实际变化范围为:
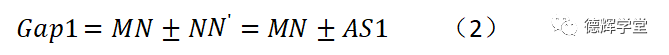
MN就是数模上的理论间隙。
EF处缝隙Gap2的实际变化范围为:
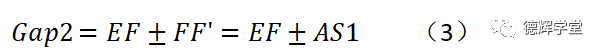
EF就是数模上的理论间隙。
再强调一次,上述公式(2)和公式(3)没有考虑旋转带来的影响,也没有考虑零件制造误差,变形之类的其它因素。如果要考虑,需要叠加进去。
接下来,我们再来讨论副定位孔销浮动AS2对Gap1和Gap2带来的影响。
显然,AS2是对旋转的“纵容”。我们先不考虑主定为销的平移,仅仅看AS2带来的影响。见动画5:
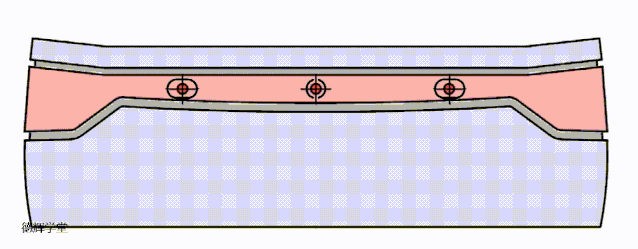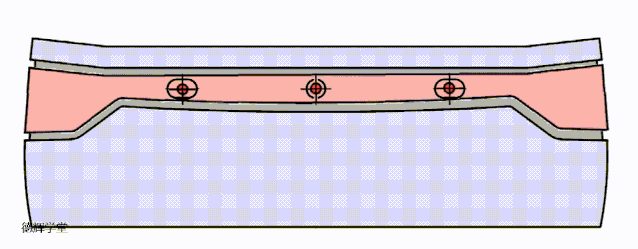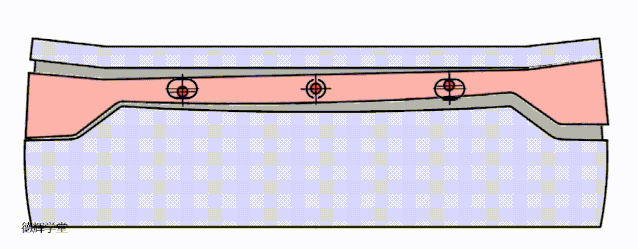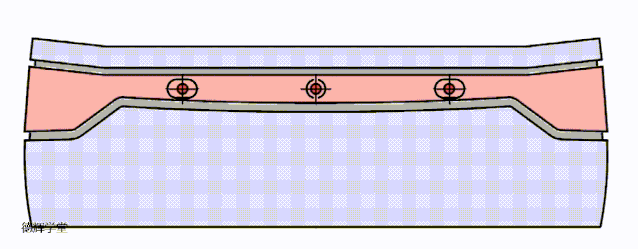
动画5 副定位特征的孔销浮动带来仅旋转
副定位销孔之间的孔销浮动AS2会带来旋转。同样,我们把动画5中的旋转再夸张一点,先来研究MN处的间隙Gap1.
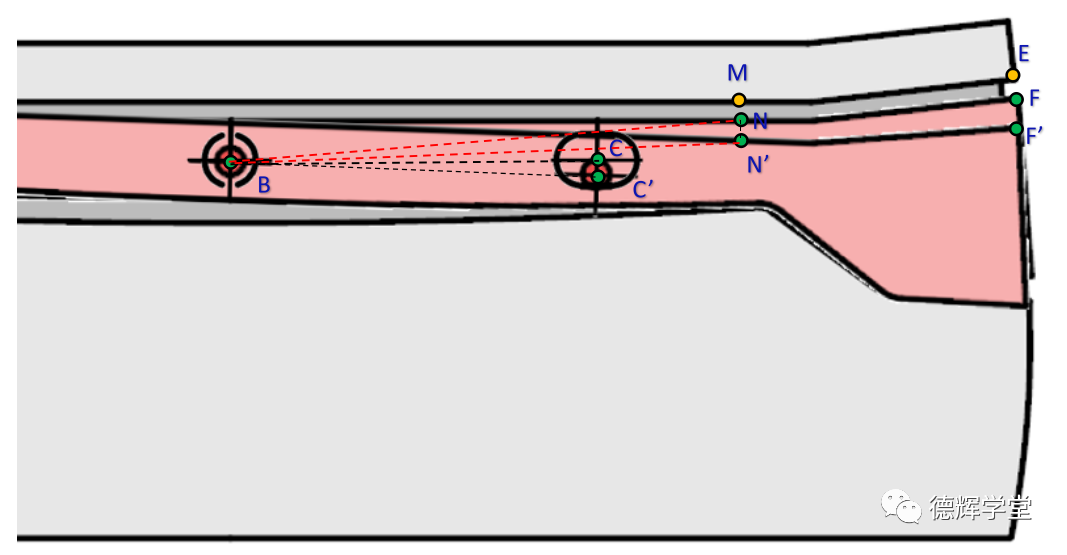
图9 MN处的几何关系
见图9,B为灯带上的主定位销(假设没有移动),C是灯带上的副定位销,C’是旋转后灯带的副定位销。根据图9所示,显然有三角形BCC’和三角形BNN’为相似三角形(都是等腰三角形,顶角相等)。则有:
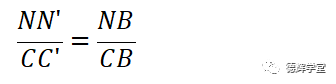
又因为CC’为原因变量(孔销浮动), 而NN’为结果变量(被动引起间隙变化),那么N点处的缝隙变化量相对于C点处孔销浮动的敏感度则为:
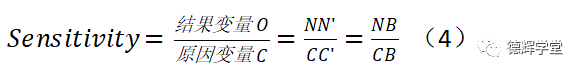
我们还可以把公式(4)做一个变换:
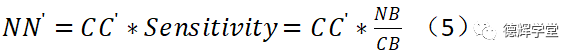
假设副定位销处的孔销浮动是AS2, 即有CC’=AS2。我们就可以算出N点处缝隙变化量NN’。根据公式(5),不难算出NN’的大小:

注意,公式(6)和公式(4), NN’处的变化量来源于副定位销处的孔销浮动AS2,但是,还必须要乘以一个系数, 就是敏感度Sensitivity, 而这个敏感度的大小取决于N点的具体位置!
我们凭直觉或者根据公式(4), 甚至可以预测,F点处的变化量会更大!
我们先来计算MN处的实际缝隙Gap1。
因为NN’是相对于理论缝隙MN的变化量,它可能是正的,也可能是负的,所以最终的Gap1,则是把MN加上这个NN’或者减去这个NN’,那么最终MN处的实际Gap1的范围不难可得出:

基于同样的逻辑,我们可以计算EF处的缝隙Gap2:
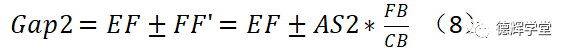
好了,整了一大堆看似装逼,实则简单的公式,我们终于计算出来了MN和EF处的缝隙变化范围。
注意,目测图9中的位置,无能是N点处的敏感度(Sensitivity=NB/CB),还是F点处的敏感度(Sensitivity=FB/CB),它们都大于1。
就是这些要命的敏感度,放大了孔销浮动带来的影响!
当然,当敏感度小于1的时候,它可以缩小孔销浮动带来的影响。这,对我们的设计工程师来说,有重要的意义!
关于敏感度影响的逻辑图,先看看图10:
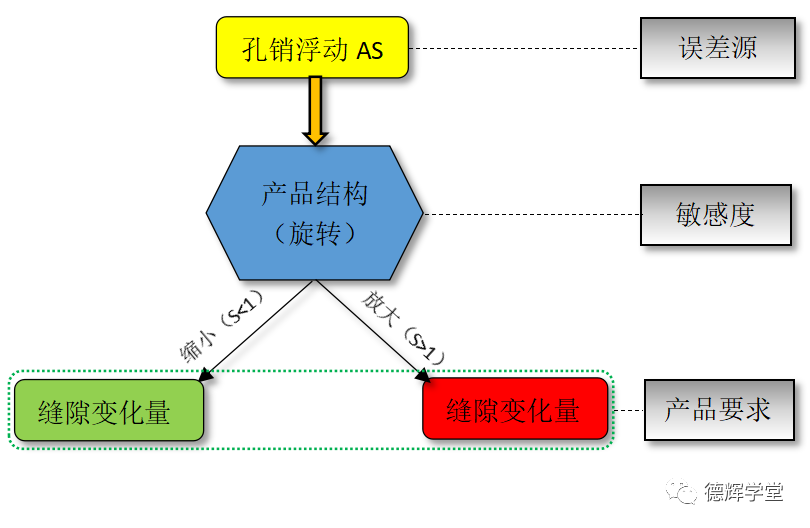
图10 敏感度影响逻辑图
假设根据公式(7)和公式(8)计算出来的Gap超出了要求,作为设计工程师该怎么解决这个问题呢?
见图10中敏感度影响的逻辑图。要想使得产品合格,即想让Gap满足DTS要求,有三种办法:
1. 减少误差源,比如收严孔轴的尺寸公差,减少孔销浮动;
2. 降低敏感度,比如设计工程师改变结构设计;
3. 降低产品的要求,比如放宽DTS要求;
上面三种方法,哪种方法更加靠谱呢?第一种方法,贵;第二种方法,麻烦;第三种方法,找抽。
现实中,要根据实际情况综合考虑。作为设计工程师,我们这里主要讨论如何通过改变结构设计来满足DTS要求,也就是采用第二种办法(在开模之前,这是最经济,最靠谱的方法)。
接下来我们详细讨论。
3.2 改变设计来降低旋转的影响
前面我们介绍过,我们为什么害怕旋转?因为旋转可能使得敏感度S大于1,这样会放大原因变量。当然了,旋转也可能使得敏感度小于1,削弱原因变量的影响。
作为结构设计工程师,我们的本能应该是,只要有旋转运动的场合,我们就要想尽一切办法降低结构的敏感度S。
就本期文章的案例而言,如何降低敏感度?先直接上图吧:
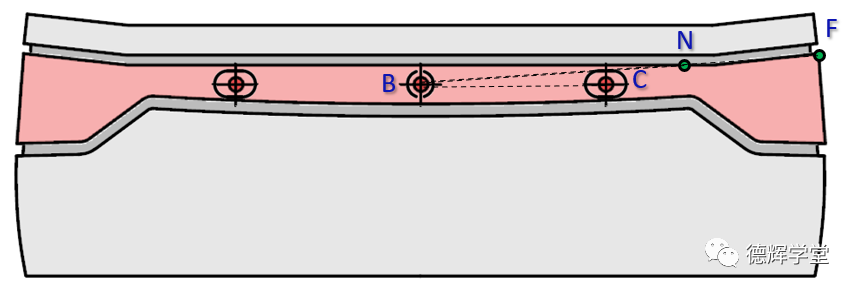
图11 原始设计
如果你是设计工程师,根据公式(7)和公式(8),我们知道:
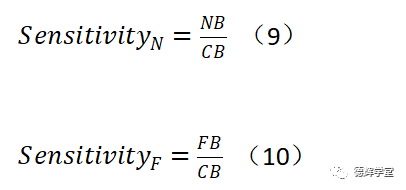
根据上面两个公式,如果NB和FB的长度很难改变,要想降低敏感度,那就是让分母变大呗。也就是增加CB的长度就能使得敏感度降低。
如何增加CB得长度?废话少说,直接看动图吧。
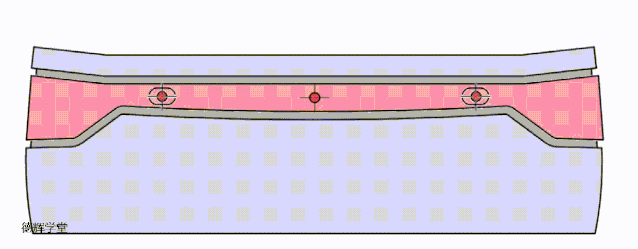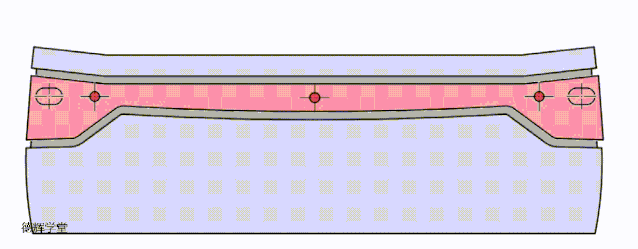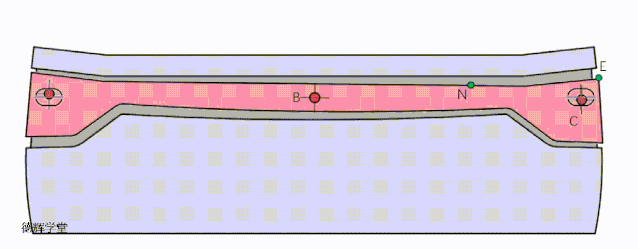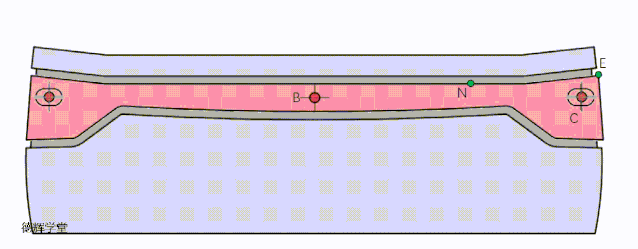
动画6 改进定位方案一
见动画6,我们就是把副定位特征和主定位特征之间的距离,使劲拉开,使得CB变大,从而达到降低敏感度的目的。
是不是So easy?
其实,对很多老道的结构工程师,尺寸工程师或工艺工程师来说,都会有意识的拉开定位特征之间的距离。其根本原因就是为了降低敏感度。
上面的方案还可以优化吗?其实还是可以的,见下面动图。
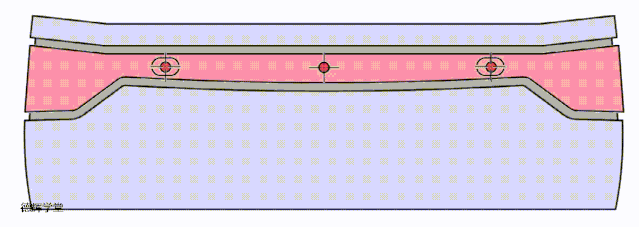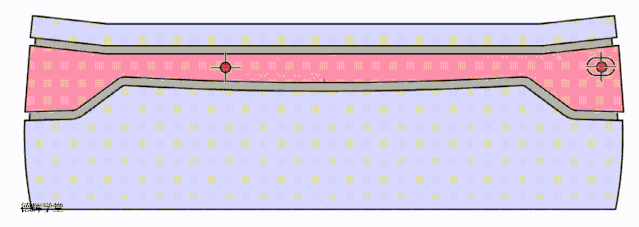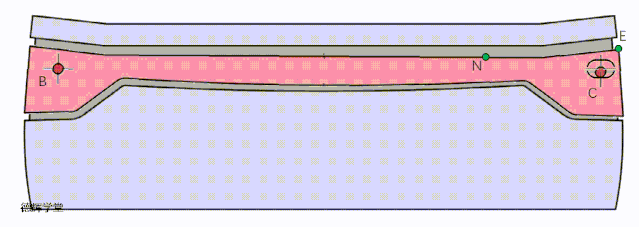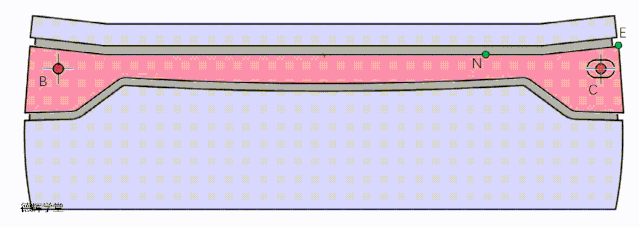
动画7 改进方案二
见动画7,将定位特征更改成一个主定位特征加一个副定位特征后,再把两定位特征之间的距离拉开,这样的定位效果会更好。
细心的小伙伴可能会问,动画7中的定位方案和动画6中的定位方案相比较,貌似对F点和N点的影响没有太大变化?
两种方案,对F点和N点的影响差异确实不大,但是,动画7的方案,对左侧(再强调一下,是左侧)缝隙处所有的点有利的。
为什么呢?
因为左侧缝隙处所有的点,他们对副定位特征孔销浮动的敏感度都小于0.5, 右侧缝隙处所有点的敏感度也就在0.5到1之间。
这个几何关系,聪明的你用直觉是不是可以感觉到?要是实在感觉不到,就拿公式(9)和公式(10)去套吧。
好了,到这里,我们讨论了三种定位方案,为了让各位小伙伴直观的感受三种方案的效果,我们把三种定位方案的动图放在一起,大家可以直接比较一下:
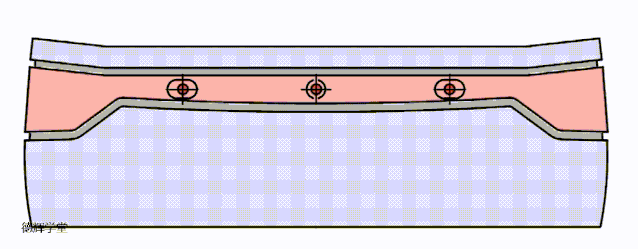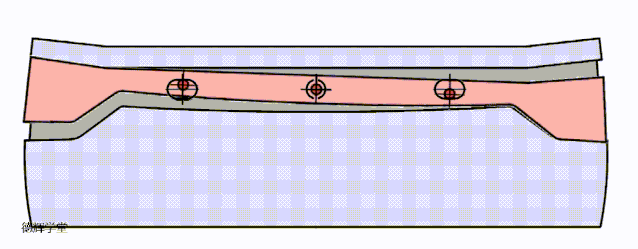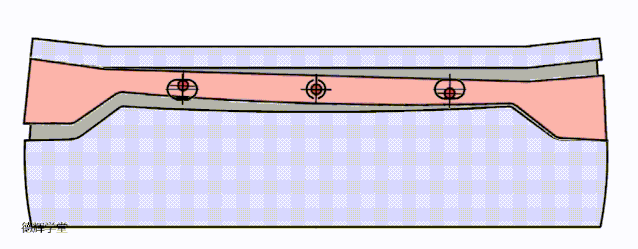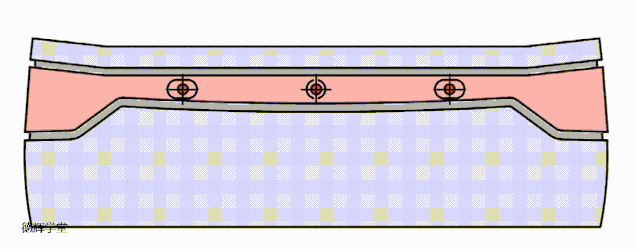
A原始方案

B 改进方案一
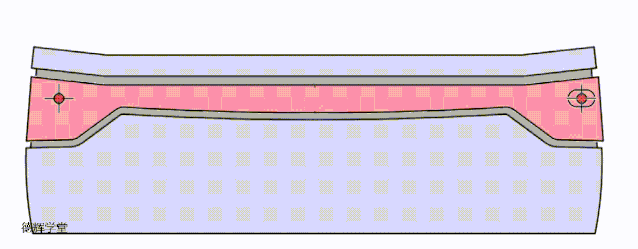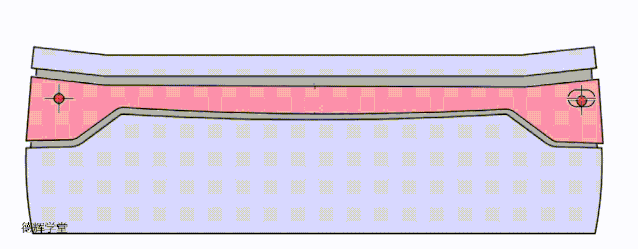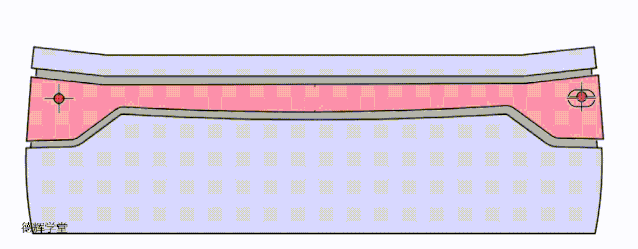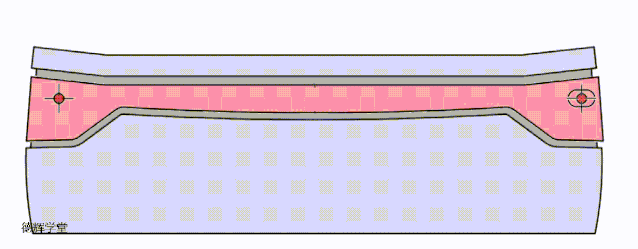
C 改进方案二
动画8 改进方案比较
希望有兴趣的小伙伴,仔细比较动画8中3个方案的特点,这是本期文章的核心。前面唧唧歪歪讲了半天,就是想说明,根据旋转的特点,我们如何利用这种特点来改进设计,所以有了这三种方案。
这里要稍加一些补充说明:
1) 动画8中,我们只讨论了副定位特征处的孔销浮动,引起的旋转,以及这个旋转带来的影响。没有考虑主定位特征处的平移,事实上,平移和旋转是需要要叠加起来的。不过这并不影响本文的结论,因为平移对谁都是公平的,不会改变方案之间的优劣式。
2) 动画8中的方案,我们所有的分析,并没有考虑力学方面的因素。比如,现实中,改进方案二可能有缺点,那就是灯带的变形可能会比较大(中间没有可靠的支撑),因为定位特征如果要受力的话,距离拉的越开,对变形的控制就越不利。作为设计工程师,需考虑再增加辅助定位之类的,或自己综合权衡。再多一句嘴,现实中,零件变形和公差控制是我们工程师都必须要考虑的因素,很多现场经验比较丰富的工程师,往往依靠自己的经验来反对或者揶揄公差分析工程师,或者不重视GD&T控制,这是不可取的。
4. 旋转和稳健性设计
稳健性设计,又叫鲁棒设计(Robust Design), 这是一个大的话题,我们今天粗粗过一下,它的定义是这样的:
鲁棒设计是产品在制造或者使用过程中,当结构参数,内在结构或外部环境发生变化时,都能够保持其质量的稳定性。
啥意思呢?一句话,就是产品的质量对其它的因素不敏感。比如,前一节讲的案例,如果我们能设计一种结构,使得灯带和后背门之间的间隙对孔销浮动不敏感,那么这种结构就满足稳健性设计。

图12 稳健性示意图
图12中,就希望绿色的产品质量对所有蓝色的影响因子不敏感。
用动图表达如下:

动画9 稳健性设计
动画9显示,所有的红框处的影响因子如果都在规定范围内任意变化,它对绿框处的质量肯定会有一定影响,但是无论这些影响因子怎么排列组合变化,幅度如何,产品质量变动都在一定范围内,轻微的波动,但是肯定不会超差,所谓“稳”如泰山,这就是稳健性设计的含义。
稳健性设计,说起来容易,做起来却没那么容易,对设计工程师来说,往往意味着后边包含着巨大的,看不见的工作量(辛苦了,苦逼的设计工程师们)。
顺便说一句,我们设计工程师为什么要搞尺寸链计算,公差分析?他们就是在验证自己的设计是否满足稳健性设计。
又有工程师会问,如果不搞稳健性设计会怎样?
还能怎样,废品率高呗,被客户投诉呗,售后返修率高,没生意没市场呗,反正产生的窟窿都是要用钱去堵的。
回到本期的案例,我们利用旋转的特点,改进结构设计,降低了产品缝隙对孔销浮动的敏感度,使得灯带和后背门之间的缝隙对孔销浮动不敏感,这就是在一个方面上满足了稳健性设计。
好了,本期讨论的话题就到这里了,有任何问题,或者有对文章不同意的观点,欢迎您给我们留言!
本期内容回顾
本期文章讲解了旋转对设计的影响,本文以灯带和后背门为案例,分析了由副定位特征的孔销浮动引起的旋转,对灯带和后背门缝隙的影响,并从数学上论证了当结构的敏感度大于1的时候,孔销浮动对缝隙的影响是非常大的。本文又提出了基于旋转特点,改变结构设计的两种优化方案,使得最终敏感度小于1,削弱孔销浮动对缝隙的影响。
最后,本文结合稳健性设计的设计理念,指出利用旋转减少结构敏感度就是在提高产品的稳健性。
最后说明,和往期的GD&T知识普及性文章不同,本期文章和上期文章都属于探讨性文章,里边的错误和不严谨的地方在所难免,欢迎您给我们留下您的意见。
在本文最后的最后,留一道思考题给你,本文提出了改进的方案一和方案二,见图13,对于缝隙的最大缝隙和最小缝隙之差,即均匀度或平行差来说,那种方案更好呢(不考虑可能存在的变形问题)?欢迎您给我们留言!
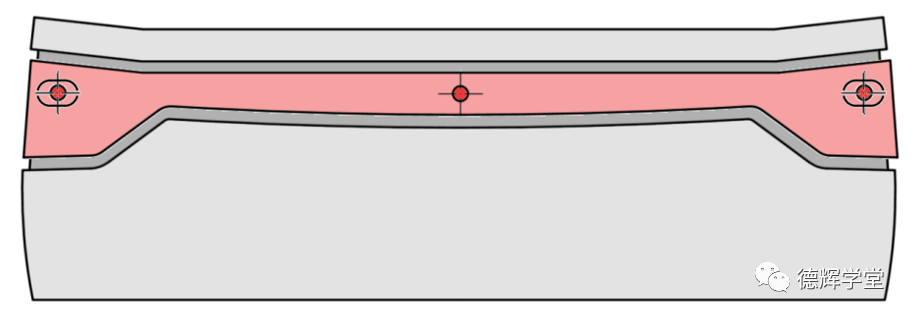
A.改进方案一
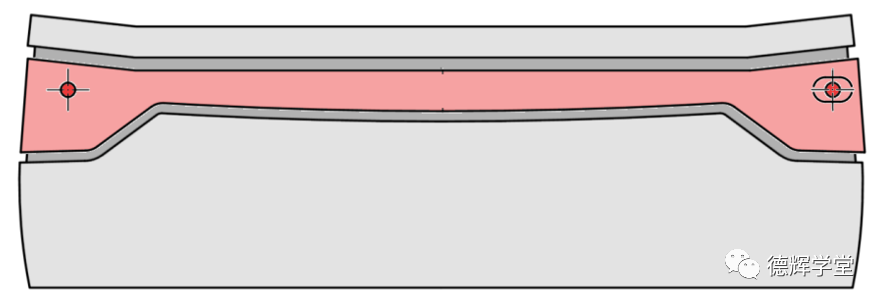
B.改进方案二
图13 哪种改进方案对控制均匀度最有利?
【后记】
本文还有很多问题可以继续挖掘。比如,如何计算孔销浮动的量?平移和旋转如何叠加?计算缝隙的时候如何结合零件图上的几何公差?敏感度Sensitivity一般多大合适?如何利用概率分布来计算间隙大小的概率分布从而判断合格率?如果我们已知某处的变形量我们又如何处理?
不管你关心还是不关心,这些有价值的问题就在那里,需要有人去回答。
软件是个好东西,它帮助我们避开复杂的计算,为我们节省了很多时间,同时软件也把我们给宠坏了,它让我们懒得去思考后边最基本的几何原理和关系。鼓励发烧友们继续探讨,你甚至可以把你的见解整理成文章发给我们,一经录取,我们是有偿发表哦。
觉得文章不错?点个赞呗,不想点?转发朋友圈也行啊!


取消回复