我们为什么害怕旋转(第一章)?
在我们现实的3D世界中,平移和旋转是最常见不过的运动方式,就公差世界来说,这两种运动方式给我们带来的影响却是截然不同的。
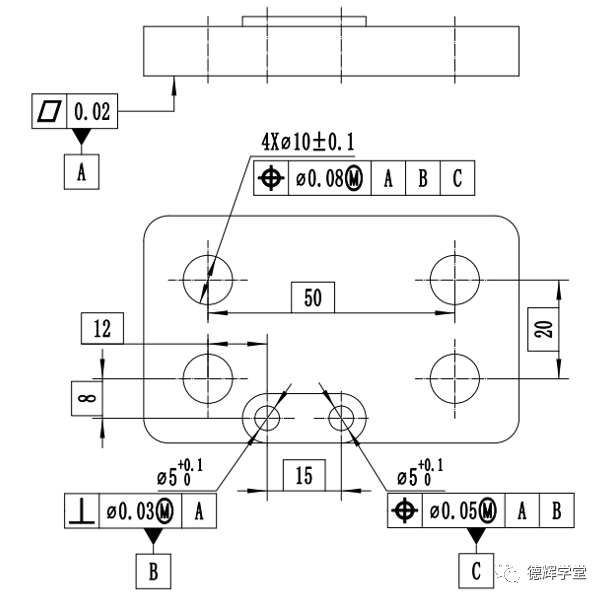
话不多说,大家看看下面这张2D零件图:

图1 2D标注案例
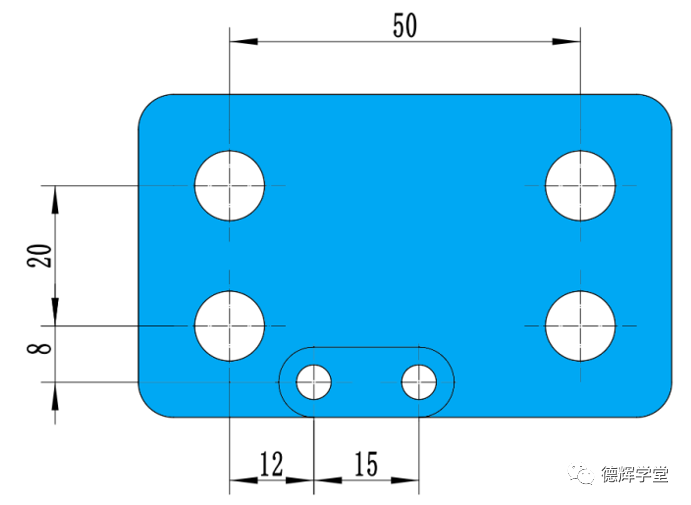
图1是一张看起来平淡无奇的2D图纸,如果我们只讨论红圈处4个孔的位置度,你能看出来有什么不对劲的地方吗?
对很多年轻的工程师来说,不一定能看出其中的问题在哪里,相信很多老道的测量工程师,一眼就可以看出来其中的不爽之处:那就是在测量的时候,会出现图1中右上角的那个孔(蓝圈部分)的位置度误差会比其它三个孔的位置度误差要大(很容易超差),而且该孔的位置度会非常不稳定的现象。
为什么呢?
说到底,都是“旋转”惹的祸!
今天我们就这个话题,来一次深入探讨。本期文章的话题将分为4个部分:
-
平移,旋转和敏感度
-
旋转对测量结果的影响
-
旋转对设计的影响
-
旋转与稳健性(Robust)设计
因为篇幅太长,本期文章只放送前两章,后两章下次放送。希望对这个话题有兴趣的小伙伴能够耐心的阅读完。
1. 平移,旋转和敏感度
平移和旋转的特点相信大多数小伙伴都很清楚,但是我们还是需要重新认识一下。为了能够帮助大家理性的认识平移和旋转,一开始我们就需要建立简单的数学模型,详细阐述一些简单的基础理论。
1.1 平移和敏感度
假设有一个刚性连接杆(刚性就是不会变形的意思),它现在的运动方式就是朝某个方向纯粹的平移(见下图动画)。
根据平移的特点,不管它是朝哪个方向平移,该连接杆上任意两点移动的距离都是相等的。
动画1 平移
比如,在该连接杆上有两点,分别是A点和B点。假设我们推动了B点,使得连杆发生了平移,那么B点由原来的位置移到新的位置B’点,同时,连杆上的另外一个点A点也会移动到新的位置A’点。见图2。

图2 连杆平移
因为是我们推动了B点,使得B点发生了位移,位移长度为BB’, 而A点和B点在同一个刚性连杆上,B点发生了位移, A点必然也会发生位移,显然,A点的位移为AA’。
我们再做一个定义,推动B点后,产生了位移BB’, 我们把BB’称为原因变量C(Causal Variable), 而AA’是因为我们推动B点产生位移BB’后被动产生的,我们称AA’为结果变量O(Outcome Variable)。
这样的表达是为了说明,一个是因(原因变量),一个是果(结果变量)。
很多时候,人们比较关心结果变量AA’和原因变量BB’之间的关系。我们再引入一个新的名词,叫敏感度S(Sensitivity)。
敏感度S就能够体现原因变量C和结果变量O的这种关系。怎么体现呢?它们满足下面这个公式:

在图2的平移过程中,显然有AA’=BB’。所以可以推算出:

敏感度S为1, 就意味着B点变化多少,A点也变化多少,没有放大,也没有缩小。
所以在平移的运动过程中,重点是结果变量和原因变量之间的关系比值是1,即敏感度为1。
在平移的运动中,敏感度为1好像理所当然,没啥好稀罕的,为啥非要装逼兮兮的弄一个公式呢?
别急,在另外一种运动中,敏感度就可能不是1了,比如说,旋转。
1.2 旋转和敏感度
旋转的运动方式大家都容易理解,纯粹的旋转就是一个刚性物体围绕一个固定点进行转动。
还是拿连接杆为例子,假设该刚性连接杆围绕C点做旋转运动,如下图中的动画所示:

动画2 旋转
同样的假设,我们不小心推动了B点,把它推至B’点,使得连杆围绕C点旋转,然后导致A点会移动到A’点, 见图3:

图3 连杆旋转
基于我们前面的定义,显然BB’为原因变量C,而AA’为结果变量O。此时敏感度S为:
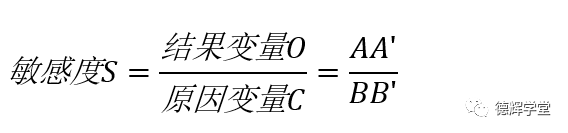
利用图3中的相似三角形关系,不难计算出敏感度的具体值:
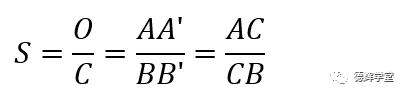
显然,这个敏感度的大小取决于图3中AC和CB的长度之比,实际上也就是取决于C点的具体位置。
目测图3中C点的具体位置,可以确定的是,敏感度S一定大于1.
这个敏感度又什么意义呢?
它可以帮助我们计算出结果变量。
假设,我们经过计算,得到S=1.8, 如果B点移动了1mm, C点的移动量一定是1.8mm的。我们可以将公式(1)做一个简单的转化:

注意,公式(2)是我们经常会用到的公式,敏感度很多时候由结构决定,原因变量我们可以模拟或者假设,但是结果变量是需要被计算出来的,那就是由公式(2)来计算。
我们为什么害怕旋转?就是因为在旋转运动中(平移不会有这种情况),结果变量O相对于原因变量C的敏感度S可能会大于1, 或者可能大于2,甚至更多。这样可能会导致结果变量变得更加大,给我们带来意料之外的负面影响。
当然,敏感度S也可能会小于1,让结果变量缩小,我们在优化设计,或优化工艺的时候,可以考虑利用这一点。
讲到这里,很多小伙伴可能开始懵圈,你究竟想说啥?
不要着急,我们慢慢来,现在我们开始回到本文刚开始时提出的案例,来慢慢分析。
2. 旋转对测量结果的影响
我们先再来看看本文的案例:

图4 本文案例
图4中采用位置度公差,管控4个孔。在加工过程中,4个孔的加工工艺是完全一样的,比如采用加工中心将4个孔在一道工序里加工出来。但是,在测量的时候,我们还是会发现每个孔的位置度大小是不一样的。
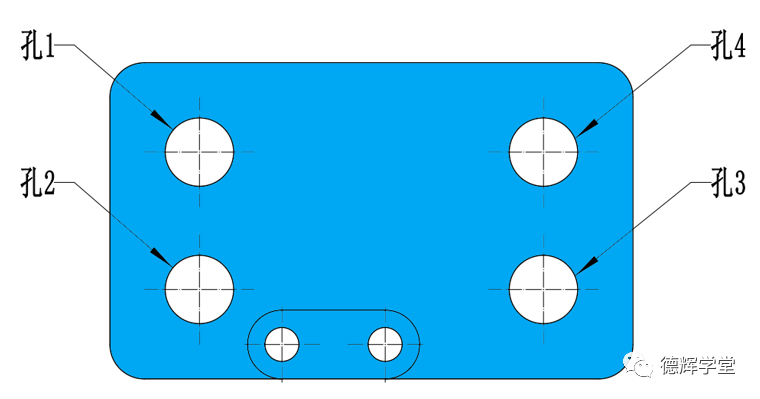
图5 被加工4孔
见图5所示,大量的测量数据表明,孔2的测量结果往往会是4个孔中最小的,而孔4则是4个孔中最差的。直觉比较好的小伙伴,甚至可以直接得出以下规律(大概率):
位置度_孔2 < 位置度_1 < 位置度孔_3 < 位置度_孔4
为什么呢?
接下来我们就来仔细分析分析。
为了让分析更加严谨,摒弃其他干扰因素,我们再做进一步假设。假设工艺工程师采用加工中心,并采用最短路径的加工工艺(公差累加最少),即将基准孔B,基准孔C,及被测孔1至孔4一起加工出来(一次装夹),而且我们又假设加工的误差全部来自于机床本身的精度误差,不考虑工装夹具,产品变形,测量误差等因素。
加工中心有自己的坐标系,我们把它叫机床坐标系好了。注意,加工时用的机床坐标系和测量时用的基准坐标系不是同一个东西。
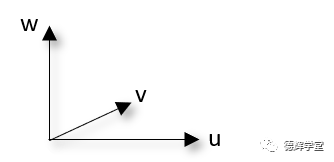
A. 机床坐标系
B. 基准坐标系
图6 机床坐标系和基准坐标系
如果我们连机床本身的精度误差都不考虑,认为机床是绝对理想的话,又不考虑其它因素,那么加工出来的2个基准孔中心位置和4个被测孔的中心位置坐标,一定和机床坐标系中设定的坐标是完美重合的。

A: 加工中心设定孔的位置
B: 加工中心加工出来孔的位置
图7 加工中心的设定和加工完美一致
如图7所示,所有加工出来的孔的位置都与加工中心设定的坐标完全重合,那么加工出来特征之间相对的方位关系肯定是完美的,四个孔的位置度误差一定是零。
现在我们开始考虑机床本身的精度误差。
那就意味着加工出来的这6个孔的位置和机床坐标系中设定的理论位置会有偏差。见下图中的动画:
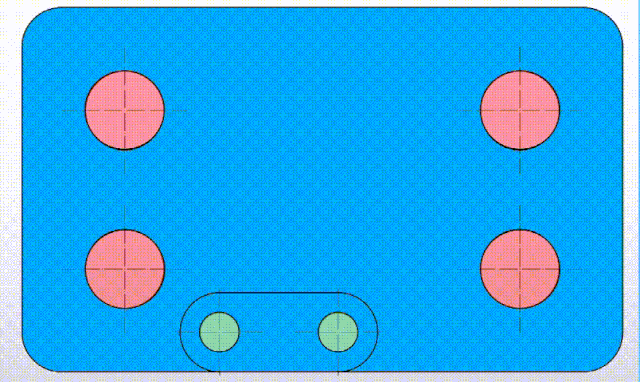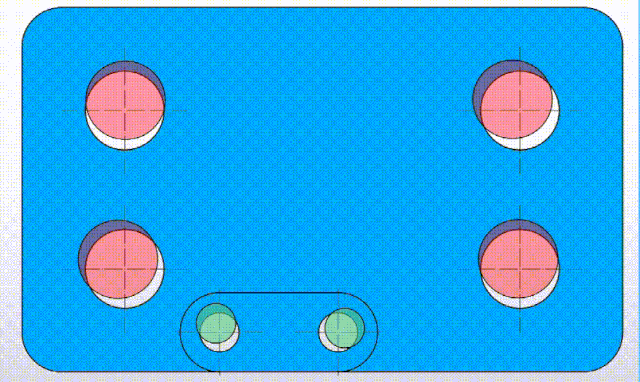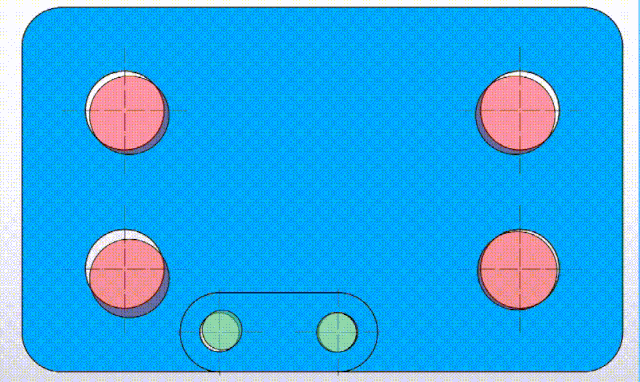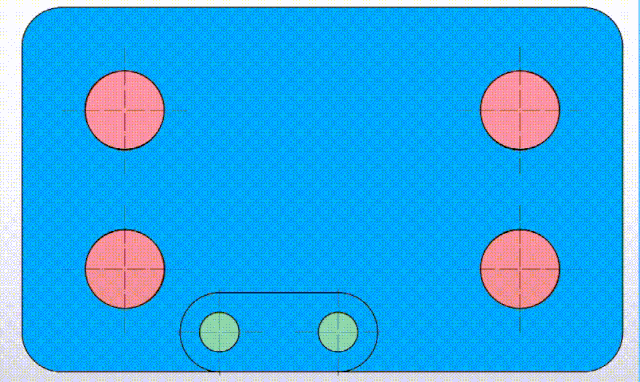
动画3 机床加工精度引起的误差
动画3中显示了机床在加工6个孔的时候,因为机床的精度问题,会导致每个孔的实际位置和机床程序设定的坐标有点偏差(实际上这个偏差很小),对于这种机床精度原因引起的偏差我们还可以合理的做一下假设:
1. 机床在加工六个孔的时候,相对于机床坐标系,每个被加工孔可能的最大偏差基本一样,都是d(deviation);
2. 六个孔的实际偏差方向(相对于机床坐标系)是各自独立而且是随机的;
事实上,4个被测孔本身,基准孔B以及基准孔C被加工“偏”后,对4个被测孔的位置度都有影响,而且这些影响又都不一样。
所以本节我们再分3个小节来分别讨论。
1. 4个孔自身被加工偏后对测量结果的影响
2. B基准孔加工偏后对测量结果的影响
3. C基准孔加工偏后对测量结果的影响。
以上三种情况是我们对加工零件时,复杂的误差源经行的初步分解和分析,下面我们就一一来讨论。
2.1 4个孔自身被加工偏后对测量结果的影响
第一种情况,我们先假设B,C基准孔在加工的时候,没有误差,它们的实际位置和机床坐标系设定的位置是重叠的,即基准是完美的(基准平面A的偏差可以暂时不考虑,它的影响对每个孔是都是公平的)。此时,4个被测孔中,每个被测孔的几何误差完全来自于机床本身的精度误差。
如果BC两孔的实际位置和机床坐标系设定的位置是完美重叠的,那么基准坐标系xoy和机床坐标系uov就呈现理想的相对关系(就是说两个坐标系相互之间仅仅理论偏离了设定的某个值),见图8。
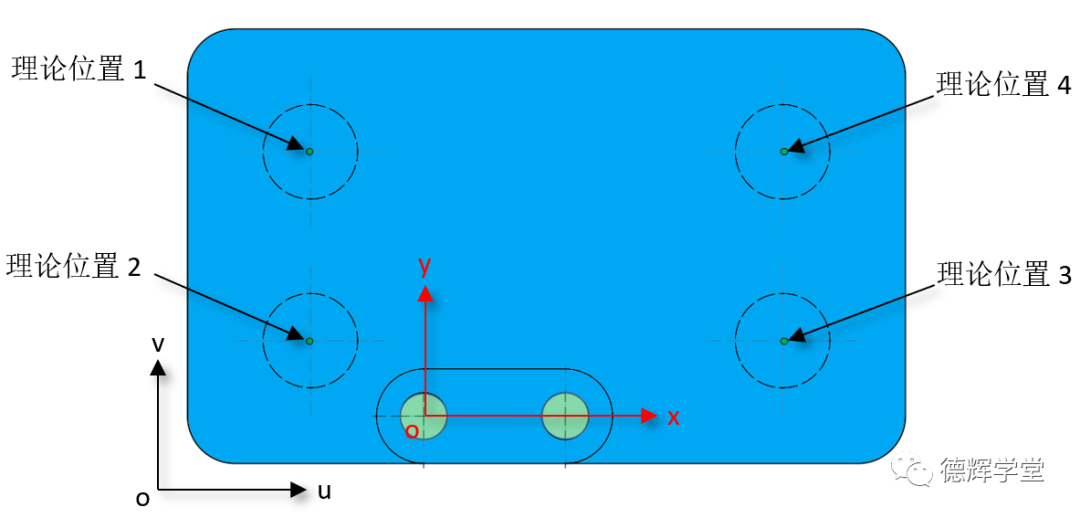
图8 机床坐标系,基准坐标系和理想位置
因为机床坐标系和基准坐标系相互之间的关系是理想的,那么在机床坐标系里边,4个被测孔的设定位置就是基准坐标系的理论位置了(即理想要素的位置),见图8。
现在,加工出来4个孔的实际位置和理论位置(机床设定位置)有偏差了。
4个被测孔的实际位置相对于机床坐标系设定位置的偏差分别是ds1, ds2, ds3, ds4,相互比较而言,4个孔相对理想位置的偏差,应该都是一样的(概率上)。即有:
ds1 = ds2 = ds3 = ds4
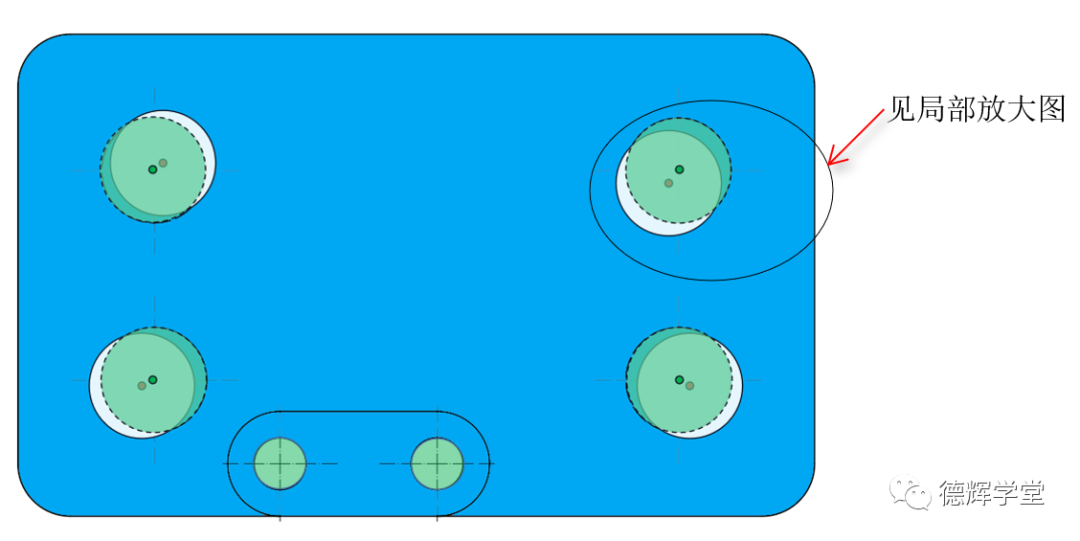
A. 机床设定位置和加工后孔的实际位置

B. 局部放大图
图9 四个孔的偏差概率相同
如图9所示,孔4的实际位置度误差为DS4(DS4=2*ds4),每个孔的实测位置度分别为DS1, DS2,DS3, DS4。
相互比较而言, DS1,DS2,DS3,DS4之间的差异很小(概率上)。
根据第一章节的理论,容易看出,4个被测孔的实际位置度误差是一个结果变量,而其原因是由机床的加工精度造成的,所以机床精度是原因变量。
在本文中,我们对机床的精度dm再做一个简单的定义,它表示机床加工出来的孔的实际位置和机床程序设定的坐标位置的最大偏差。
显然,就图9中的工况而言,有:

也就是说,加工精度dm和实际位置度的偏差是相同的。
注意,为了和机床精度dm做同量的比较,本文中都采用位置度的半值误差,即位置偏差(单边)来作比较。
基于本小节的假设,加工精度和实际位置偏差之间的关系是1:1的关系:
O结果变量 = 实际几何误差(半值)=ds
C原因变量 = 机床加工精度=dm

就是因为每个被测孔的位置度的半值误差或位置偏差对加工精度的敏感度S=1,所以机床精度对每个孔影响一样的(众生平等)。
这里稍微再强调一下,机床精度对每个孔的影响一样,并非意味着每个孔的实际位置度(即位置度误差)就是一定一样的,只是说明每个孔的实际位置度都在同样一个范围内变化而已(它们的概率一样)。
2.2 B基准孔加工偏后对测量结果的影响
为了使问题简单化,我们重新做假设,我们先认为4个被测孔的位置不变,即加工出来4个孔的位置刚好和机床坐标系重合。仅仅B孔的位置因为加工精度的原因在变化(先不考虑C,我们认为C孔和B孔保持理想的方位关系)。见图10:
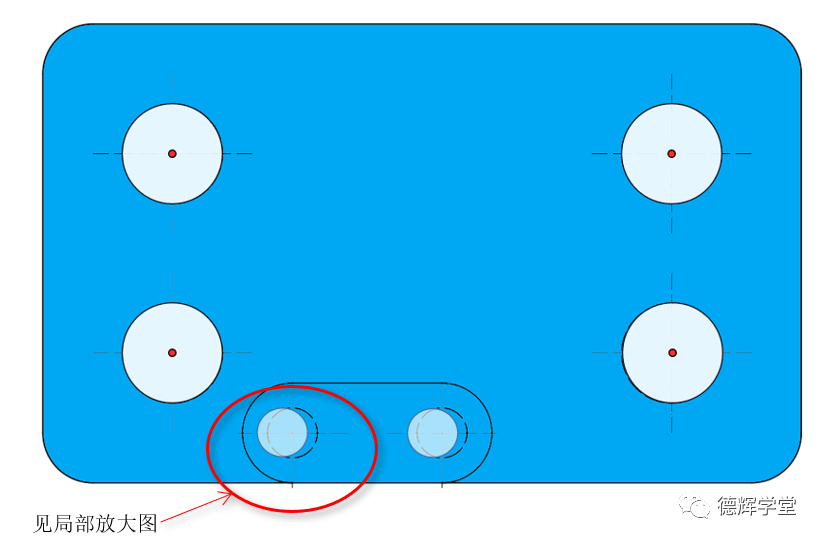
A. 加工歪了的B基准孔
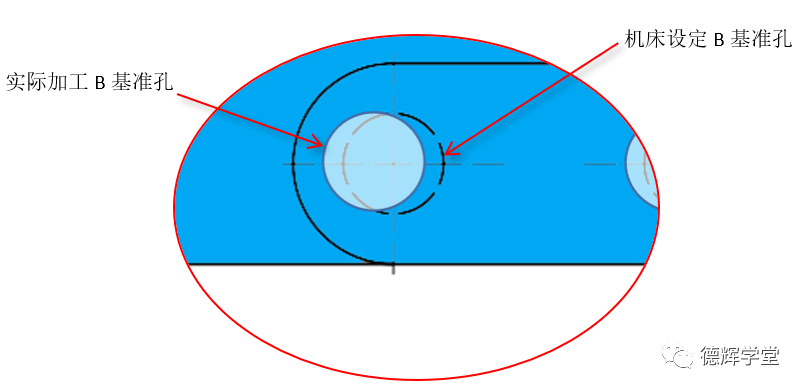
B. 局部放大图
图10 加工歪了的B基准孔和局部放大图
如果B基准加工歪了后,带来的后果是是什么呢?
俗话说,上梁不正下梁歪, B作为基准要素如果位置跑偏了,对以它作为基准的其它被测要素就会有影响,比如说,四个被测孔。
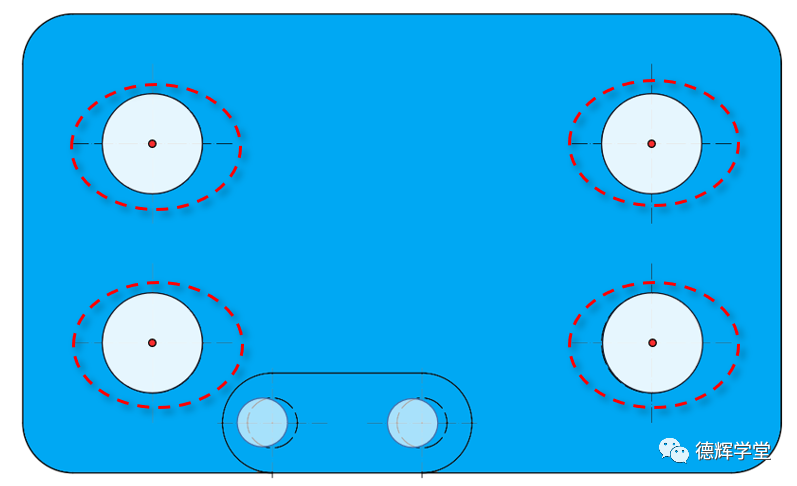
图11 被影响的4个被测孔
实际加工出来的B基准孔相对于机床设定的位置如果跑偏了,对四个被测孔的测量结果是怎么影响的呢?影响的敏感度如何?
注意,我们在分析这个问题的时候,做了很多假设(避免捣糨糊),我们认为图11中四个被测孔的位置和机床设定的位置刚好符合,目前只有B基准加工偏了(C基准先不考虑)。
我们再稍微回顾一下基准系的功能,基准系的功能是干什么用的?
基准的功能是用来约束公差带自由度的。
从评价的角度来考虑的话,基准系的功能是用来约束理想要素的自由度的。
关于基准系功能的这两种解释并不矛盾,因为公差带的中心就是理想要素。
所以,基于基准系ABC的功能,我们不难得出,A基准要求四个孔的理想要素(4根理想的轴)和基准A保持理想的垂直关系,而B基准则要求四根理想要素要和B基准保持理想的距离关系,C基准则是联合B基准约束了四根理想要素的旋转方向。
A. 原始图纸

B 抽取出来的基准和理想要素
图12 基准和理想要素的关系
见图12,理想要素1,2,3,4作为特征组,他们和基准ABC保持理想的方位关系。红色的基准xoy坐标系是由BC构建而成,对于B基准来说,特征组必须要和基准B在x方向保持12,y方向保持8的关系,见图12中红圈部分。
注意,这个12和8是绝对理想的。而且,无论实际零件做得怎样,理想要素和基准B都必须保持这个12和8的绝对位置关系。
也就是说,如果这个基准孔B加工“歪”了,它会导致理想要素跟着一起“歪”。见动画4:
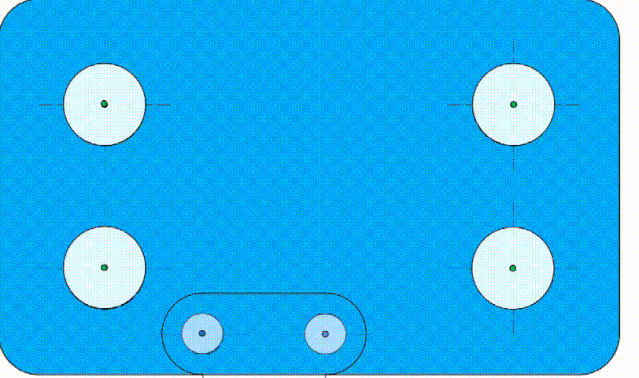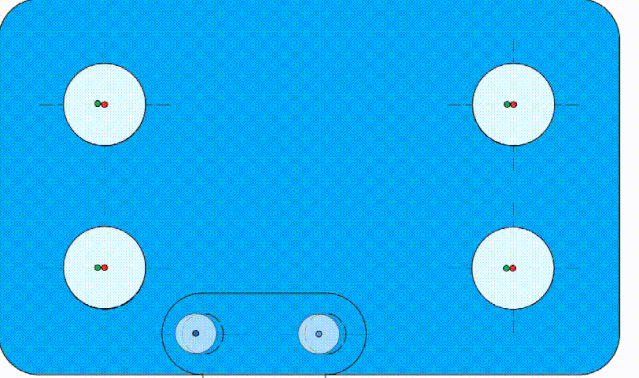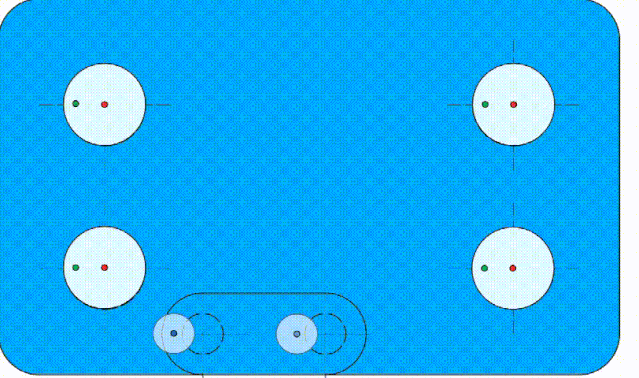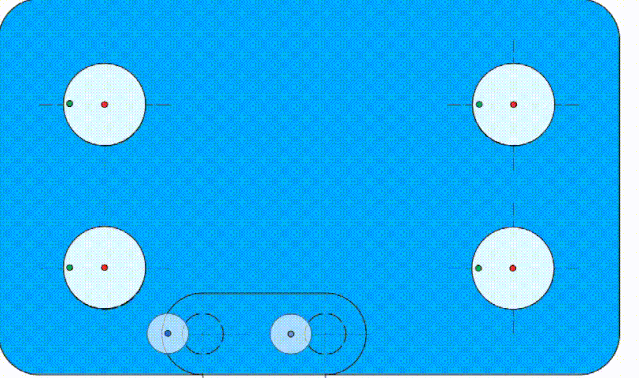
动画4 理想要素和基准一起“歪”
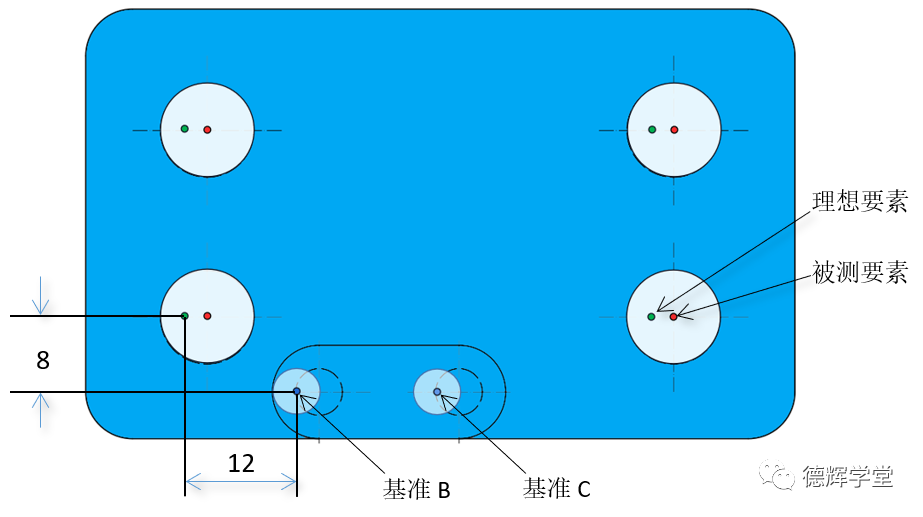
图13 理想要素和被测要素
图13中,因为机床精度的原因,导致B基准孔偏了,则它的轴线,基准B也偏离了轨道,而理想要素又和基准B穿同一条裤子,所以理想要素也会偏离。这样导致被测要素和理想要素之间就有了偏离。
在基准系ABC中, 根据基准系的功能分析,B基准约束的是理想要素(公差带中心)平移的自由度,所以如动画4中所示,基准B平移了,理想要素也会平移。
根据平移的特点, 显然,所以基准B平移多少,理想要素也就平移多少。见图14:
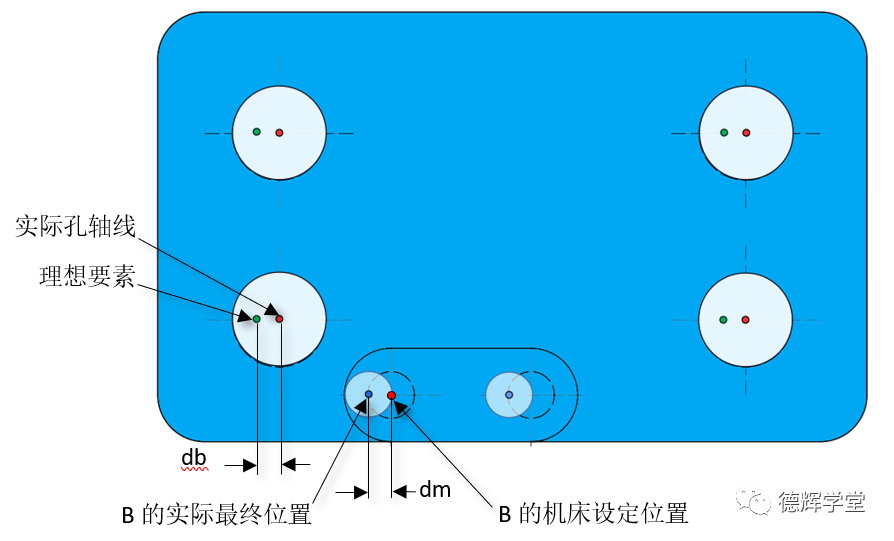
图14 基准和理想要素的偏离
如图14所示,如果基准孔B的最终位置相对机器坐标系中设定的位置偏离了dm(机床精度dm对6个孔的影响都是一样的), 那么必然会带动理想要素相对于机器坐标系偏离db, 因为是平移的原因,所以显然有:

我们还可以计算出敏感度:
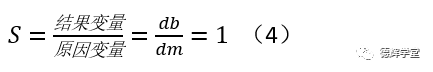
这就是说,基准孔加工偏了,对被测孔是有影响的,但是没那么恐怖,只是1:1的影响了。
我们还可以把公式(4)做一个转化:
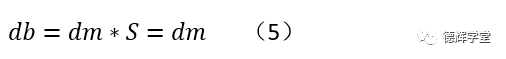
公式(5)表达的就是,基准B加工歪了后,对被测孔位置偏差带来的影响。
我们再来看看第3中情况,如果基准孔C加工偏了,对被测孔有多大的影响。
2.3 C基准孔加工偏后对测量结果的影响。
同样,我们再来做个假设,假设4个被测孔,基准孔B加工出来的位置和机床坐标系是完美一致的,只有基准孔c加工偏了。见下面动画:

动画5 基准C加工偏了
啰嗦一句,可能有些小伙伴开始觉得不爽了,你的假设不可能发生啊?哪里只有C偏的现象?不急,我们现在是分解,后边我们再综合起来分析。
因为基准C的功能是约束理想要素旋转的自由度,如果基准孔C的偏离方向是围绕B旋转,那么它会带动整个基准坐标系旋转,从而使得理想要素也跟着旋转。
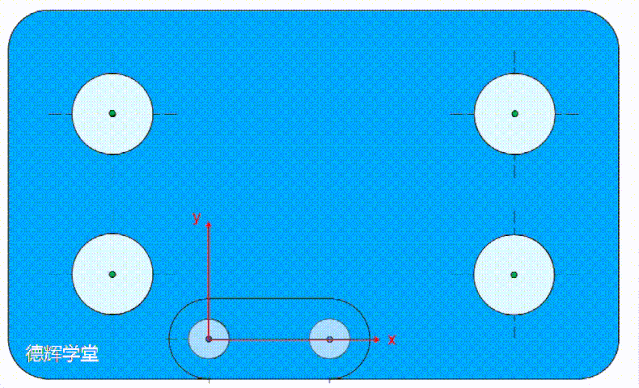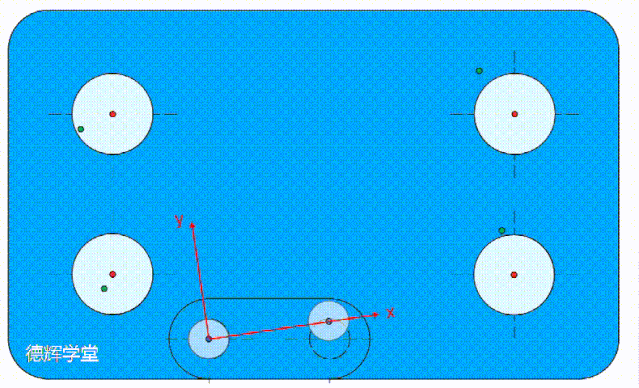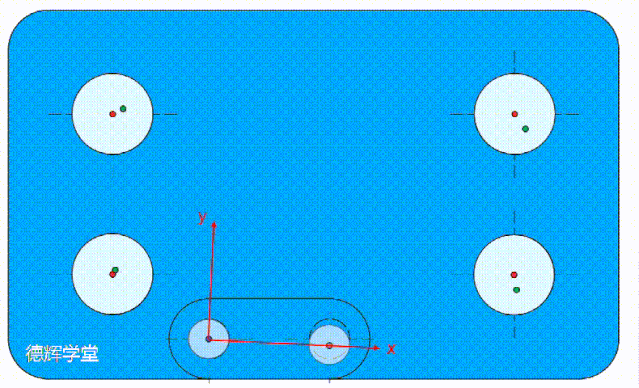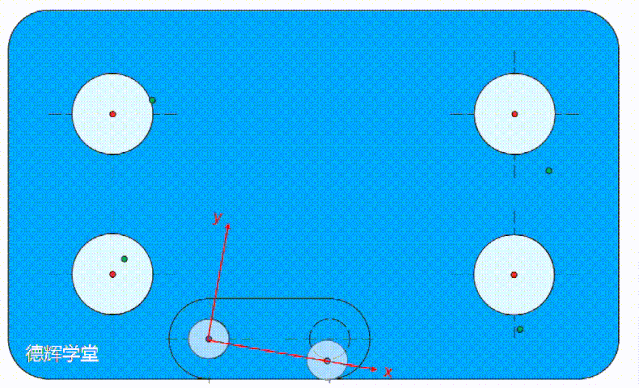
动画6 基准C带动理想要素偏
动画6中,基准C决定了基准坐标系的旋转。其中,B是坐标系的原点, x坐标轴一定过基准C, 所以基准C如果有点扰动,坐标系可能会旋转。
动画6中的示意图,我希望你多看几遍,它是本文的核心。
还有,坐标系旋转,必然会导致理想要素旋转(再啰嗦一下原因,因为理想要素必须要和基准系ABC保持绝对的方位关系),所以四个被测孔的理想要素(绿色点),也跟着旋转。
理想要素和坐标系一起旋转,而实际被测孔不动(这是我们的假设),那么必然就会导致实际被测孔轴线,即动画6中的红点,和理想要素(绿点)开始貌合神离,有嫌隙,即偏差。
请你仔细观察动画6中每个孔的偏差(红点和绿点的距离)。
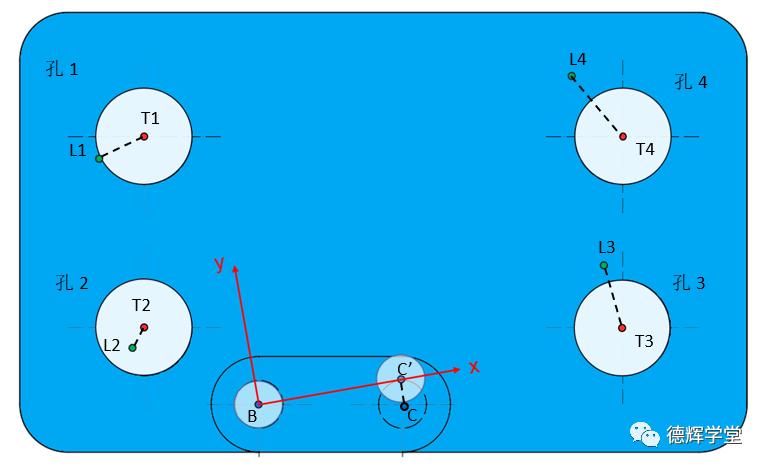
图15 基准C偏差导致各孔的理想要素偏差
由图15可以看出,因为机床精度dm的原因,基准孔C的中心如果由机器设定位置C点偏歪到C’点,即有:
CC’ = dm
在测量的时候,它会带动基准坐标系旋转,从而使得每个孔的理想要素也会有偏移,而且这个偏移对每个孔还不一样。
孔1的理想要素偏离:dc1 = T1L1
孔2的理想要素偏离:dc2 = T2L2
孔3的理想要素偏离:dc3 = T3L3
孔4的理想要素偏离:dc4 = T4L4
目测看,孔2的偏离,即T2L2的距离最小,而孔4的偏离T4L4最大。至于原因,马上证明,大家先把动画6再看看。

图16 基准和理想要素偏差的几何关系
见图16,我们做上一些辅助线,不难得出,三角形BL1T1, 三角形BL2T2,三角形BL3T3 三角形BL4T4, 以及三角形BC’C这5个三角形是相似等腰三角形(因为顶角相等)。
基于图16中的几何关系。不难得出每个被测孔相对于基准孔C偏差的敏感度:

从上面4个装逼的公式中我们可以得出一个结论,每个孔的的实际位置度偏差相对于C偏差的敏感度是固定的,但是每个孔的敏感度大小相互之间又不一样,取决于它的相对于基准系的具体位置。
而且目测4个孔中心位置偏离的举例,我们可以得出:
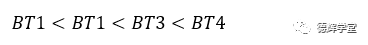
所以有:

我们再把前面4个装逼公式作一下整理,我们就可以得,如果C偏了CC’,对每个被测孔的影响偏差dc具体为:

基于BT1,BT2, BT3, BT4的不等式关系,我们可以得出下列不等式:
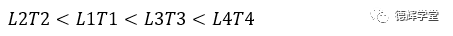
基于上面这个不等式,我们可以得出结论:
如果基准孔C加工偏了,对孔2的影响最小,对孔4影响最大。
到这里为止,我们只对复杂问题进行了单独的分解,那么如何把它们结合起来呢?
哪怕是基于我们的假设,现实中机床的精度dm对4个被测孔, B基准孔,C基准孔会同时产生影响的,如下面动画所示:

动画7 机床精度对6个孔都有影响
见动画7,机床精度对4个被测孔,B基准孔,C基准孔都会产生相同程度的影响,这些影响综合起来后,带来的后果就会使得被测孔的实测位置度变得更差!
多差呢?
实际上,最终影响就是我们刚刚分析的三种情况的叠加!结合我们刚刚分析的结果,对4个孔的实际位置的最终偏差dt(Total Deviation),我们不难得出以下公式:
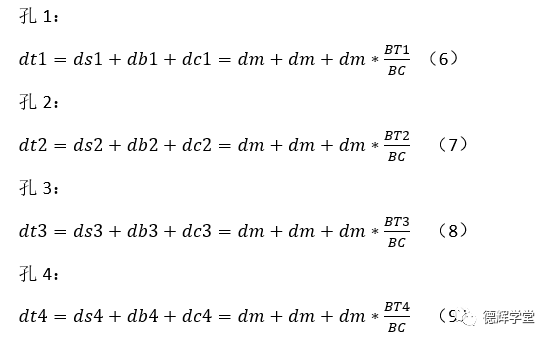
根据图纸中的几何关系,存在下面的不等式:

将公式(10)带入公式(6)(7)(8)(9)中,可以得出:
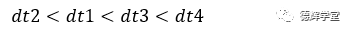
同样的原理,如果我们开始考虑工装夹具的精度,产品在加工时的变形,测量误差等因素,只要这些因素能够被量化,基于上面建立的数学模型,我们同样能够算出来对最终结果dt的影响。
篇幅原因,本期文章就到这里,我们下期再继续讨论。
本期小结:
本期文章讨论了,旋转对被测要素几何误差的影响。第一章讲解了敏感度(Sensitivity)这个概念,敏感度是个非常重要参数,它是结果变量和原因变量之间的比例系数。同时平移和转动对被测要素几何误差的影响是有区别的,平移永远是1:1的影响,所以敏感度是1,而转动则不然,它可以放大(大于1),也可以缩小(小于1),敏感度和特征的结构位置有关。
第二章,以图纸为案例,阐述了被测要素本身,B基准,和C基准被加工“偏”后,各自对被测要素的影响。并说明如果C加工偏后,对4个被测孔带来的影响更加明显。
关于我们害怕旋转的问题,不仅仅在工艺和测量上会有体现,在设计方案上也会体现,我们将在下篇文章中继续讨论,旋转在设计中的影响以及旋转和稳健设计之间的关系。欢迎您继续关注我们!
最后留一个问题给您,就本文案例而言,如果你是工艺工程师,你如何建议设计工程师修改图纸呢?如果您是设计工程师,您能看出图纸标注除了对工艺造成更大的困难以外,对设计方案还有哪些潜在的问题?
欢迎您在留言区写下您的想法。
另外,不同于以往知识点普及文章,本文只是作为一个理论探索,其中的逻辑和分析方法可能有不严谨之处,也欢迎您留言给我们指正!
觉得会文章不错,点个赞罢?不想点?转发朋友圈也行啊!

