很多时候，我们会看到零件图或者装配图采用了公差代号的标注方式，比如下图所示：

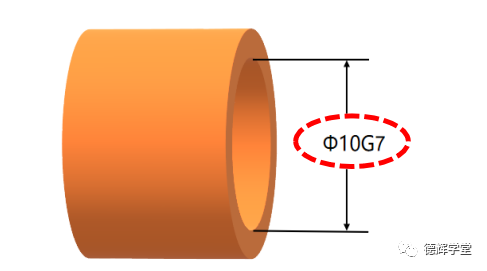
图1 零件图

图2 装配图

     如图1和图2中的红圈处的公差代号，每个数字或字母分别表示什么意思？设计工程师如何正确采用公差和合理的配合？不采用公差代号可以吗？采用公差代号对工艺工程师和质量工程师有什么意义？

     本期文章我们就来理一理这个话题。本文将分为3个章节来探讨这个内容。

     1. 两种尺寸公差的表达方式

     2. 常见的几种配合和应用工况

     3. 采用公差代号的现实意义

     对于机械专业的小伙伴来说，本章的内容纯属基础知识，希望能够通过本篇文章来夯实你的公差基础。对于非机械专业出身，但在从事与图纸相关工作的小伙伴来说，或许这正是你入门的一个机会哦。

1. 两种尺寸公差的表达方式

     我们在图纸上看到的尺寸公差，主要分为数值公差和公差代号两种，而且绝大多数是数值公差。

1）数值公差

    当设计工程师在设计一根轴的时候，他希望这跟轴的直径是Ø28，但是他又知道生产车间或者供应商做出来的轴一定不会刚刚好是Ø28（有误差存在），多多少少都有偏差，所以为了验收，他必须给出了一个范围，比如轴的最小直径不能小于Ø27.9（下极限尺寸），最大的直径不能大于Ø28.1（上极限尺寸），这个范围的大小就是0.2（28.1-27.9=0.2），这个0.2就是公差（Tolerance)。

    测出来轴的实际直径只要在Ø27.9和Ø28.1之间，该尺寸就是合格的。否则，就是不合格。

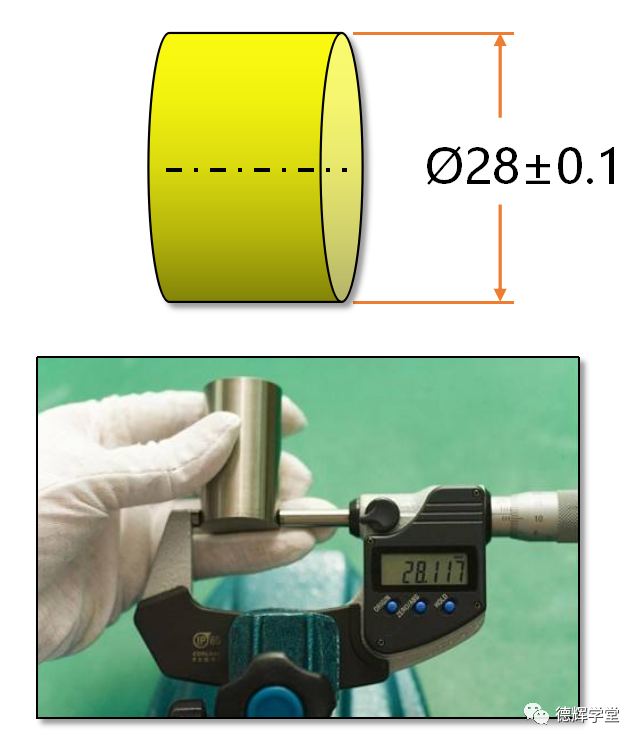
图3 图纸标注与实际零件

     显然，公差0.2表达的是范围的大小，它是一个永远为正的绝对值。

     图3中的Ø28俗称公称尺寸（也叫名义尺寸，Nominal Size），其中，+0.1表示上极限偏差（Upper Limit Deviation），它就是上极限尺寸28.1减去公称尺寸28的结果；同样地，-0.1表示下极限偏差（Lower Limit Deviation），它就是下极限尺寸27.9减去公称尺寸28的结果，具体见图4。

     写个公式吧（尽管有点讨厌）：

     上极限偏差 = 上极限尺寸 - 公称尺寸

     下极限偏差 = 下极限尺寸 - 公称尺寸

     明显地，上极限偏差和下极限偏差有明确的正负号，除了0以外都必须标注正负号。如下图所示：

图4 尺寸公差

     稍微要注意的是，上极限偏差决定了上极限尺寸，所以放在上边，下极限偏差决定了下极限尺寸，所以放在下边（这不是废话么？）。为公式控的小伙伴们再写个公式：

     上极限尺寸 = 公称尺寸 + 上极限偏差

     下极限尺寸 = 公称尺寸 + 下极限偏差

     还有，上极限偏差可以为负值，下极限偏差也可以为正值，但是上极限偏差一定要比下极限偏差大（在考虑正负值的基础上比较）。如下图：

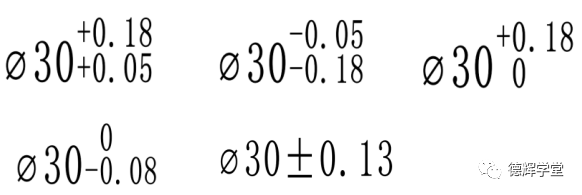
图5 尺寸公差的几种表达方式

2） 公差代号

     表达尺寸公差还有一种表达方法，那就是采用公差代号。

     比如Ø20H7, Ø15g6, 这些代号又是什么意思呢？如下图：

图6 用公差代号表达尺寸公差

     图6中Ø10G7，表达的也是尺寸公差，Ø10指的是公称尺寸，字母G表达的是基本偏差，表达公差带到公称尺寸的偏移距离（最近距离），7指的是标准公差等级是IT 7，反映的是公差大小。见下图所示：

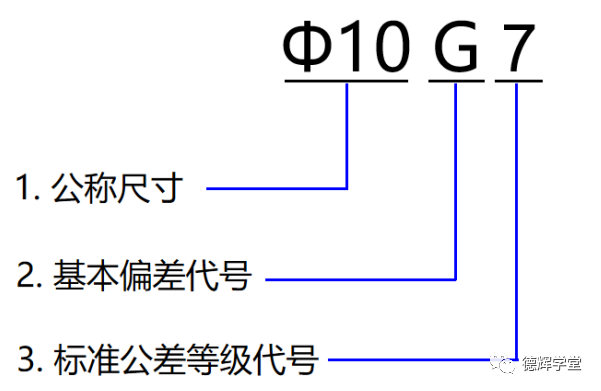
 图7 公差代号的3大要素

     图7显示的是尺寸公差基本的3大要素，即公称尺寸，基本偏差，公差大小（即公差等级）。

     图7中的公差值究竟是多大呢？还有3大要素表达的是什么意思呢？

     一般很少有工程师能记住这些代号代表的公差值（我也见过个别很牛的老法师，能记住不少公差值），实际上它是需要查表的（可以参考GB/T 1800.1），查表的知识点我们后边讲解。反正经过一番查表，我们可以得出:

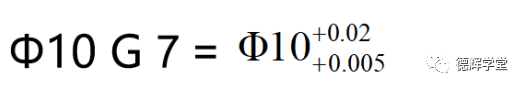
     也就是说，Ø10G7表达的就是一个尺寸公差罢了。

     我们再用图形来表达公差代号的3大要素，见下图：

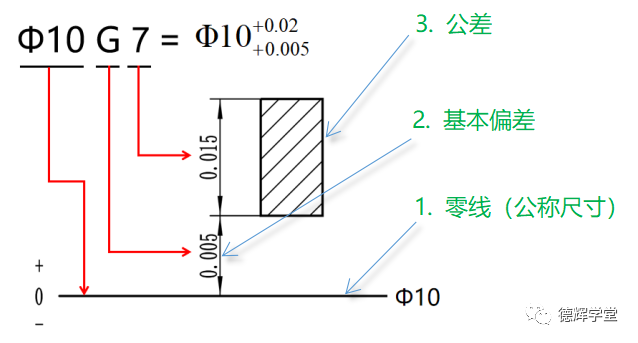
图8 用图形表达公差代号3大要素

     稍微延伸一下，这3大要素是表达尺寸公差的基本量。这3个基本量（3大要素）我们在很多地方都会用到，比如我们在讲非对称轮廓度，讲检具的基本策略和1/10原则，都是在确定这个底层的3个基本量。

     我们先来看看基本偏差字母的含义，从图9中可以看出，每个字母表达了公差带到公称尺寸即零线的距离（最近距离）。对于孔来说，一定采用大写字母，用大写字母A,B...ZC来表达偏差，为了怕混淆，字母I，L，O，Q，W没有被采用（可能是因为长相难看）。

     其中，代号A的公差带距离公称尺寸（零线）距离最远，即基本偏差最大，它在零线的上方。代号越往后边公差带越往下掉，到H的时候，公差带的下端刚好靠近零线，再往后，公差带继续往下掉，到ZC掉到最底端。见图9.

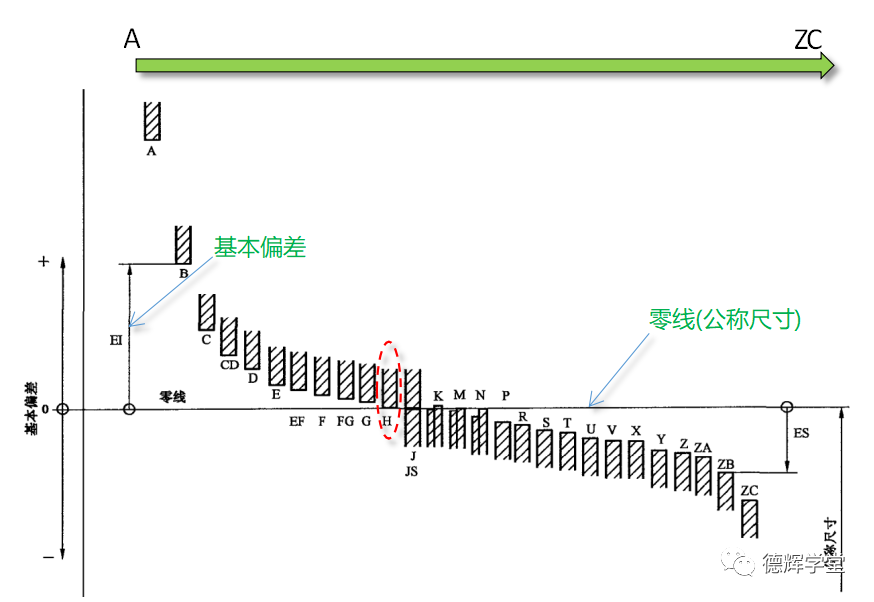
图9 孔的基本偏差

     孔的基本偏差代号特点见图9，我们比较一下Ø30A10, Ø30H10, Ø30ZC10:

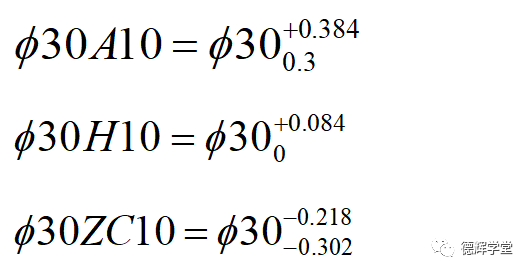
     从上面的3个尺寸公差可以看出，对于Ø30的公称尺寸来说：

     A=0.3 H=0 ZC=-0.218

     图9中，有一个特殊的偏差代号(见红圈处)，希望大家把它记住，那就是H，它的下极限偏差刚好对齐零线，永远是0，上极限偏差是正的某个数，这个数是多少，取决于公称尺寸和公差等级（后边会讲）。

     比如：

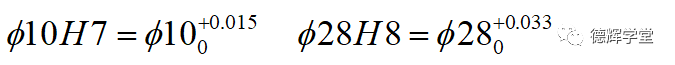
     注意到没？偏差为H的孔，下极限偏差都是0.

     而且，如果孔的基本偏差采用H， 它还可以表达一个重要的配合信息，那就是设计工程师采用基孔制配合，我们在第二章会提到。

     我们再来看看轴的基本偏差，它是小写的字母，用a,b....zc来表示，其中i，l，o，q，w五个字母因为长相难看，不被采用。

     再次强调，孔用大写字母，轴用小写字母来表达偏差。

     有小伙伴会问，两孔的中心距，台阶的高度，非孔也非轴，用大写还是小写？

     这里涉及到采用公差代号的一个前提，那就是只有尺寸要素（FOS）的尺寸，才可以采用公差代号。

     两孔中心距或台阶高度，非尺寸要素，不能采用公差代号（最好连尺寸公差都不要采用，用几何公差控制）。

     事实上，非尺寸要素的尺寸采用公差代号也没有意义，公差代号最终是为“配合”服务，而非尺寸要素是不能用来配合的。

     回到主题，和孔一样，代号为a的公差带距离公称尺寸（零线）最远，而且它是在零线的下方。代号越往后边，公差带越往上升，到代号h的时候，公差带上端和零线对齐，距离是0，再往后走继续上升，一直到zc。

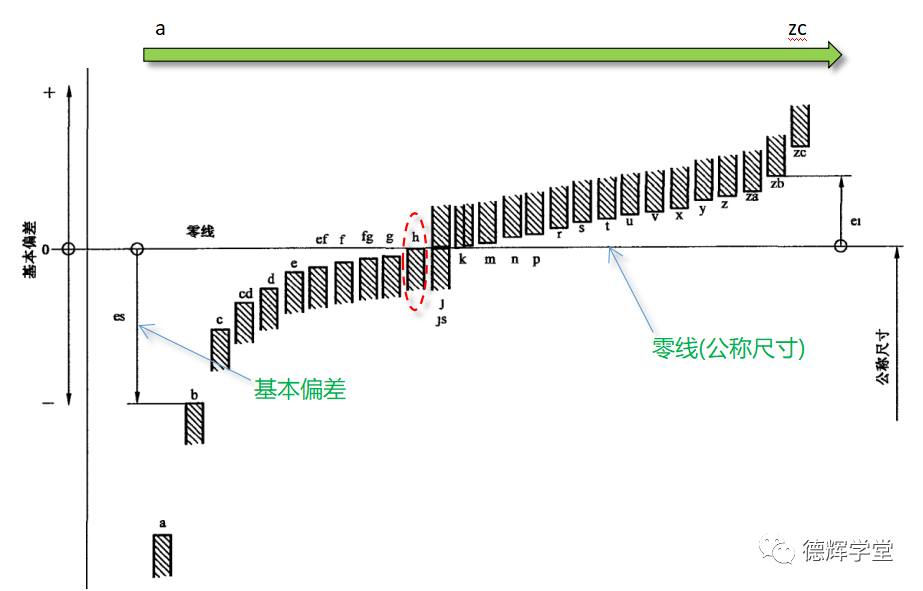
图10 轴的基本偏差

     轴的基本偏差代号特点见图10，我们比较一下Ø30a10, Ø30h10, Ø30zc10:

     不难看出，对于Ø30的公称尺寸来说，有：

     a=-0.3, h=0 ,zc =0.218

     不知道大家注意到没有，对同一个公称尺寸来说，a和A， h和H，zc和ZC对应的基本偏差数值是一样的？

     也就是说，基于同一个公称尺寸，孔和轴的基本偏差是以零线为中心，对称分布的。

     这个特点大家也要注意，这意味着同样的孔轴配合，它的表达方法不止一种。

     在图10的基本偏差代号中，也有一个字母希望大家记住，那就是h, 它的表达的上极限偏差永远是0。比如：

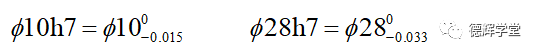
     看到没？

     设计工程师对轴的基本偏差采用h， 那就是他对孔轴配合采用基轴制（后边会讲）。

     接下来，我们再来认识一下公差等级（International Tolerance)。

     啥也不用多说，直接看表吧。

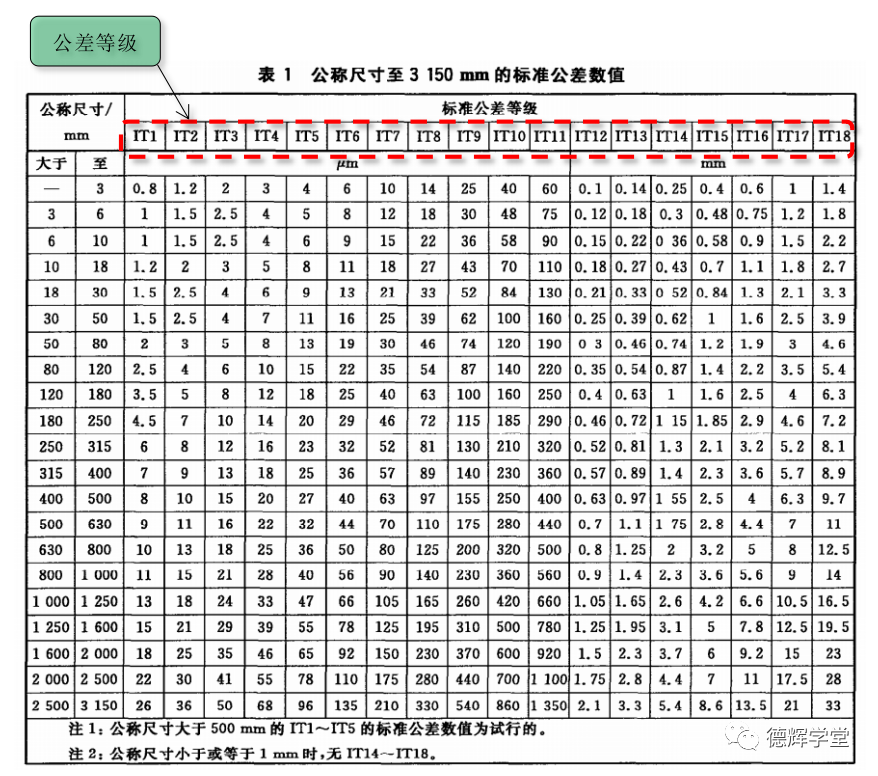
图11 公差等级

     从图11中可以看出，公差等级是从IT1-IT18, 一共18个等级。公差等级越小的，公差要求就越高，表示精度越高，逼格也越高，当然意味着价格也越贵。

     人们有时会把零件要求的精度等级和机床的加工能力对应起来，见下面的表格：

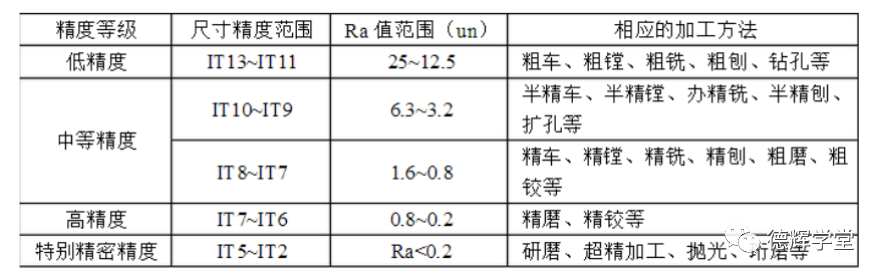
图12 零件的精度等级和加工方法

     图12中的表格，对那些刚刚入门，对机床加工精度还没有感觉，而且经常被工艺工程师欺负的设计工程师来说，还是很有用处的，可以参考，至少知道自己在设计零件的时候，放的公差是不是合理。

     如何通过公差等级得到零件的公差呢？很简单，查表。

     举个例子吧， 比如孔的尺寸公差标注为Ø25G7，其中7就表示公差等级是IT7级， 根据公称尺寸25，可以查得该孔的公差（上极限偏差-下极限偏差）为0.021，见图13。

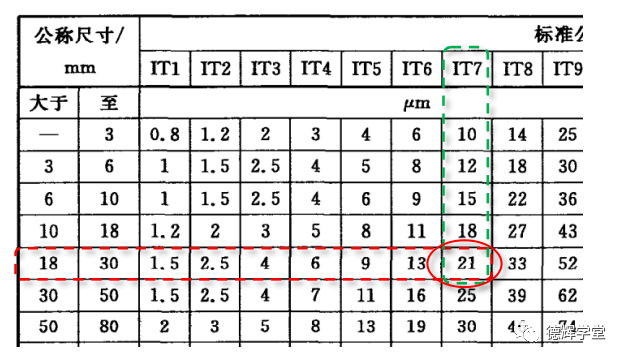
图13 根据公差等级查公差

     好了，到这里，我们做一个练习，看看Ø25G7具体的尺寸公差是多少。

     首先我们看看公差带分布的图形，见下图:

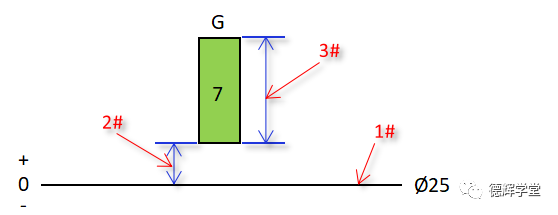
图14 尺寸公差的3个基本量

     见图14，1#表达的是零线，也是公称尺寸，显然是Ø25，3#表达的是公差的大小，由7级精度等级决定，通过图12中查表，我们已经查出来公差带的高度是0.021。

     接下来就需要查2# ，即偏差，偏差由G和公称尺寸决定。当然也是查表：

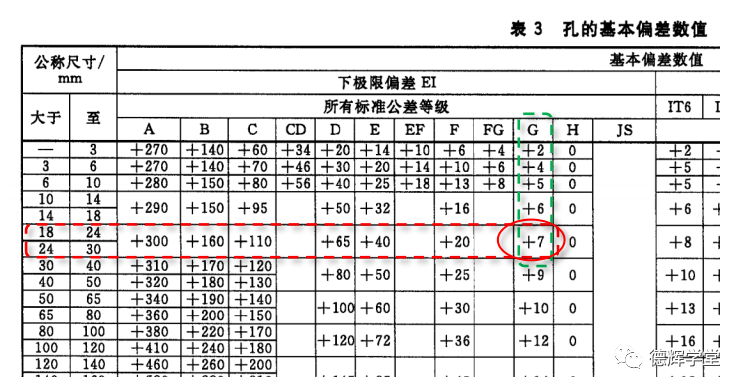
图15 根据字母查偏差

     根据图15，不难查出，偏差是0.007（注意，单位是u）。在基于图14的3个基本量，不难得出：

     下极限偏差=0.007

     上极限偏差=0.007+0.021=0.028

     最后可以得出：           

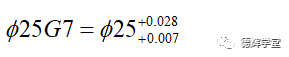
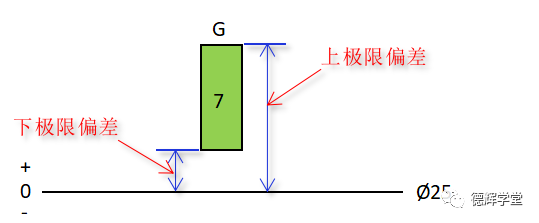
图16 两个极限偏差

     图16中表示，上极限偏差等于下极限偏差加公差。

2.常见的配合和应用工况

     我们再来谈谈配合，配合这一节内容分3个小节来讲，主要讲3种配合，配合的表达和基孔基轴制及应用工况。

1）三种配合

     配合是为了满足特定功能需求而设置的一种孔轴关系。

     常见的配合有三种，间隙配合，过盈配合和过渡配合。

间隙配合

过盈配合

过渡配合

图17 三种配合

     所谓间隙配合，孔轴之间永远有间隙，要求孔比轴大，而且孔轴配合后的最小间隙必须大于等于0，见下图：

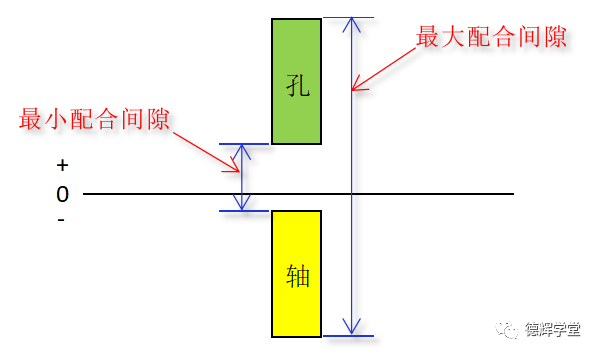
图18 间隙配合

     所谓过盈配合，永远是处于胀死状态，要求轴比孔大，而且最小的过盈量也必须大于等0. 见图19：

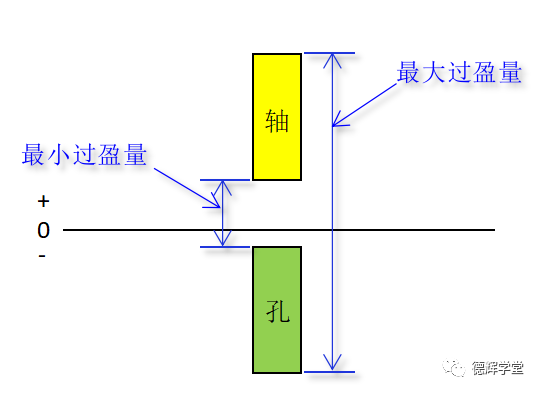
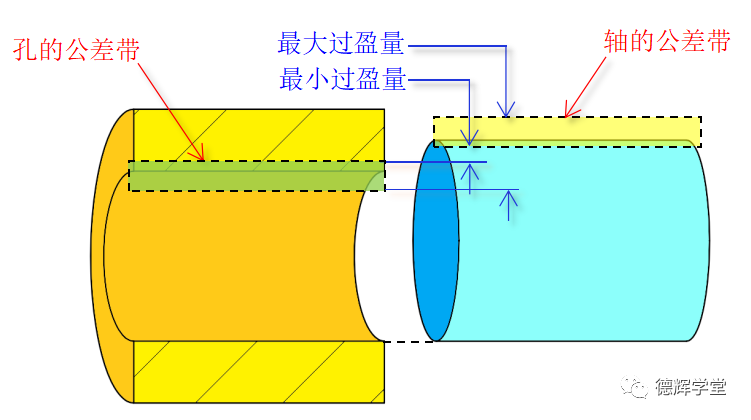
图19 过盈配合

     所谓过渡配合，就是不伦不类的那一种配合（实际上非常重要），它使得孔轴之间的配合关系，可能出现过盈，也可能出现间隙，但是不管是过盈或者间隙，他们的量都不是很大。

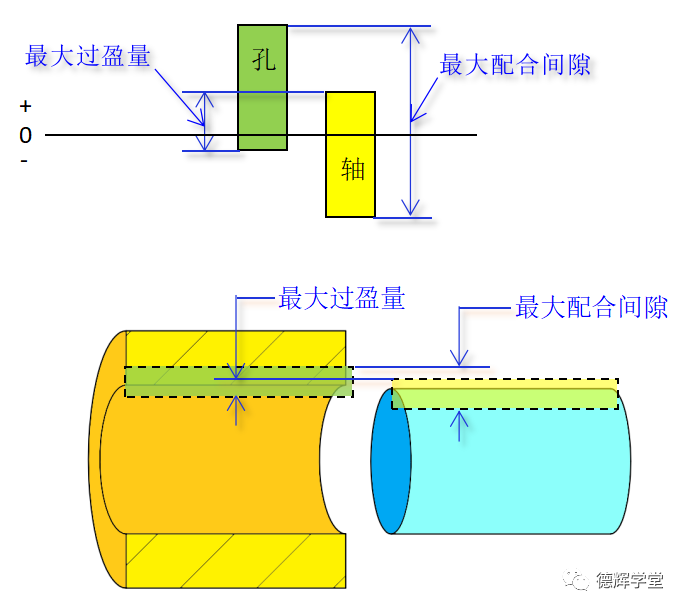
图20 过渡配合

     图18-图20显示的3种配合的情况。

2）配合的表达

     配合的本质是为了有效控制间隙或者过盈量，从而满足功能的需求。

     比如，夹具上有一个可伸缩的定位销，下端有弹簧，使得定位销能够自由伸缩。见图21：

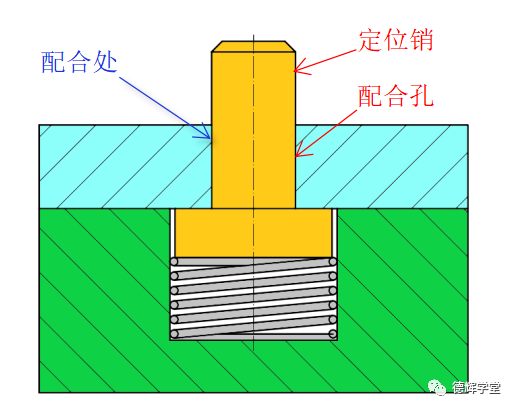
图21 孔销配合

     如图21所示，一方面希望定位销能够在一定程度上的精确定位（孔轴之间的间隙越小越好），另外一方面在弹簧的作用下，定位销能够自由的伸缩（孔轴之间必须保留有适当的间隙），应该如何设计孔轴公差呢？

     我们的机械前辈们经过理论结合实践发现，如果采用下面的配合关系，就能满足定位销的要求。会在装配图中表达如下：

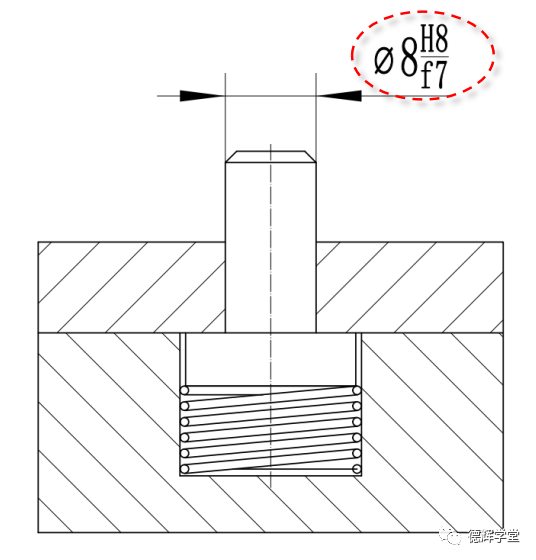
图22 孔轴配合

     图22中红圈部分表达的就是一种孔轴配合，它什么意思呢？

     它其实分别表达了孔的尺寸公差和轴的尺寸公差。见图23：

图23配合的含义

     这样控制的最小间隙是0.013，最大间隙是0.041丝，能够满足功能需求。

     注意图23中表达的配合有几个规则：

     1. 孔用大写字母表示，放在上方（有点像分子），比如图23中的H8;

     2. 轴用小写字母表示，放在下方（有点像分母），比如图23中的f7;

     3. 孔轴的公称尺寸必须一样。

     孔轴和配合的表达通常出现在装配图里，或零件图的明细栏里。

     而生产线的工程师，通过看装配图的配合信息，来决定对应的工位是否需要配压机。

     通过图纸上的配合表达，我们如何知道是间隙配合，过盈配合和过渡配合呢？以基孔制为例，见下面表格：

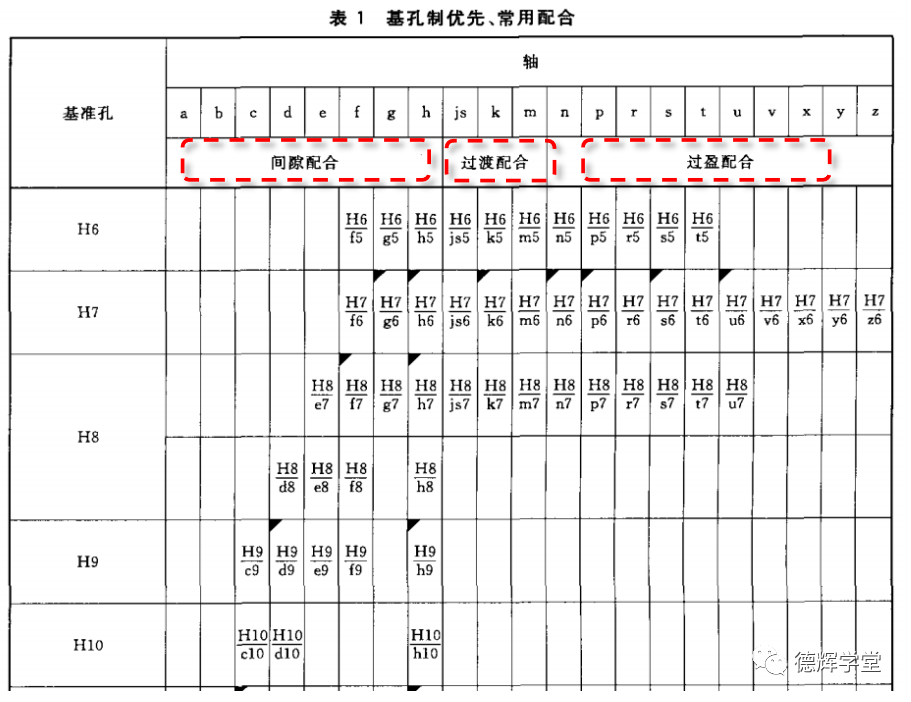
图24 三种配合

     当然，我们还有更好的记忆方法，如果小伙伴们还记得图9和图10那个基本偏差图，孔的基本偏差如果在H以前（A-H）, 这时孔的公差带肯定在零线以上，这时，如果配合轴的基本偏差也在h以前（a-h），轴的公差带肯定在零线以下，所以这时两者配合起来，肯定是间隙配合。

     比如H6/f5, H8/e7之类，肯定是间隙配合。

     过盈和过渡判断稍微复杂，如果轴的公差带全部在孔的公差带上方，那就是过盈配合, 对应的字母是n(或N)以及之后的字母。

     也就是说，只要在配合中，无论孔或者轴，偏差字母是n或者N，以及之后的字母，就是过盈配合。

     孔轴公差只要有重叠区域那就是过渡配合, 对应的字母是js, k,m或（JS K M）。

     也就是说，在配合中，无论孔或者轴，出现的偏差代号是js, k,m或（JS K M）的，就是过渡配合。

3）基孔制和基轴制以及配合的应用工况。

     在采用配合关系的时候，要么采用基孔制，要么基轴制（这就是为什么配合里边要么有H，要么有h,两者至少有一种。）。如果要采用不伦不类的既非基孔，也非基轴的话，比较怪异，很少见，查表也没法得出有用的信息，因为不利于信息传递。

     什么是基孔制呢？就是在配合中，孔的基本偏差代号是H，即孔的下极限偏差永远是零（也就是我们口头上说的，孔走上差）。在基于孔的偏差已经定下来的情况，我们再灵活的调整轴的公差，从而实现间隙，过渡和过盈配合。

     比如：

     采用基孔制的间隙配合：

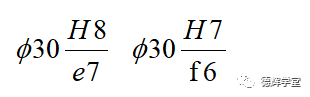
     采用基孔制的过渡配合：

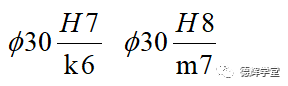
     采用基孔制的过盈配合：

     注意上面的孔的偏差全部采用H。

     那基轴制又是什么意思呢？显然就是和基孔制相反。轴的基本偏差已经明确，一定是h, 那就是轴的上极限偏差永远是0（就是我们口头上说的轴走下差）。然后再灵活调整孔的公差，从而满足间隙配合，过渡配合和过盈配合。比如：

     采用基轴制的间隙配合：

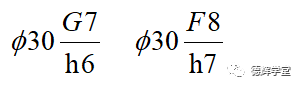
     采用基轴制的过渡配合：

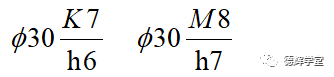
     采用基轴制的过盈配合：

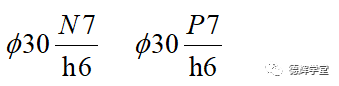
     不知道大家注意到没有，上面的配合中，孔的公差等级是不是比轴都会大一个等级，这是为什么呢？

     如果是机加工工艺的话，一般孔比轴难加工，所以会把孔的精度等级放的比轴差一些，也即是孔允许粗糙一些，轴要精细。

     这样做的目的是为了使工艺上，加工孔和加工轴的难易程度大体均衡，从而达到合理的经济性（降低成本）。不然，一个撑死一个饿死，显然不合理。

     另外一个问题是，设计工程师在设计配合的时候，选择基孔制好还是基轴制好呢？

     没有明确的答案，一般优先选用基孔制（孔难加工，尺寸容易受钻头尺寸的影响，而轴是自由的，想要多少就加工到多少。），这纯粹是从经济的角度考虑。

     不过现在机加工刀具的发展比较快，选择也很多，加工孔的各种尺寸的刀具都容易找到，选择基孔制的经济性没有那么明显了。

     还有一个情况，比如说有些通用的标准件，为了通用性（互换性），它的尺寸公差已经提前确定下来了，设计工程师只能调整其它零件的公差来将就标准件了。

     比如轴承的外圈直径公差，它的偏差是采用h, 那么在设计与轴承外圈的配合的时候，没得选择，只能采用基轴制。

     有一点需要强调的是，就配合本身而言，基孔制和基轴制没有任何本质区别。

     比如有一种非常著名的配合，叫滑配。一般销子和销套的配合都会采用滑配。

图25 销套

     如果按照基孔制，它的配合是：

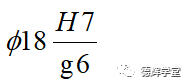
     显然，孔的公差是：

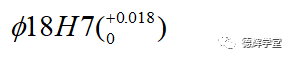
     轴的公差是：

     它的最小间隙是0.006， 最大间隙是0.035.

     如果我们把它改为基轴制滑配，它的配合如下：

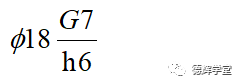
     这时，孔的公差是：

     轴的公差则是：

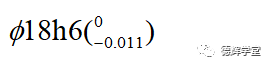
     不难看出基轴制的滑配最小间隙也是0.006，最大间隙是0.035. 即我们可以得出这么一个结论（仅仅针对配合的效果而言）：

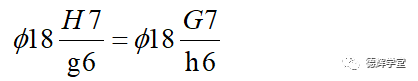
     以上这个等式为什么成立？这个问题留给各位小伙伴（提示，孔轴基本偏差具备对称性）。

     GB/T 1801有优先的配合推荐，有需要的小伙伴可以去查查。

     下图是根据ASME B4.2推荐的优先配合的解释和相对应的应用工况：

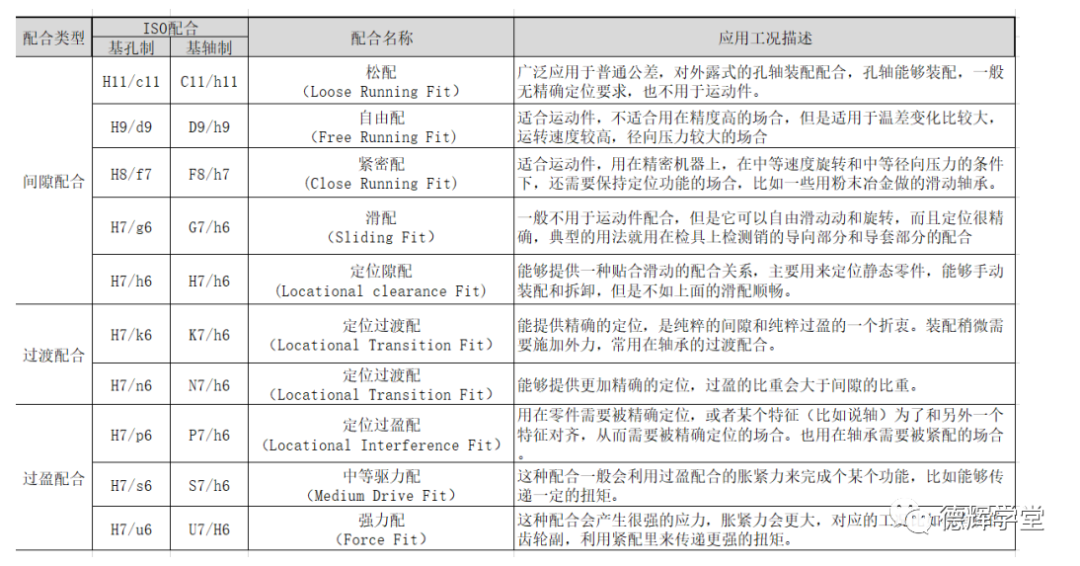
图26 各种配合和应用工况

     最后再多一句嘴，图26中所有的配合标注，都是基于包容原则，如果不基于包容原则谈论配合是没有意义的（遗憾的是，我们的标准GB/T 1800没有明确指出来这一点）。

3.采用公差代号的现实意义

     尺寸要素（FOS）的尺寸公差采用公差代号有什么好处呢？

     至少有两个好处：

1） 可以为看图人提供更多的信息，尤其是工艺工程师。

     比如设计者将轴的尺寸标注为下图：

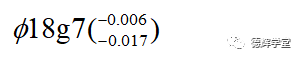
     我们就可以看出这个轴的精度等级是7级，如果要选用对应的加工设备，就必须选择加工能力在7级以上的。

    这里再多说一句，如果设计者把轴的尺寸直径标注成Ø18g7，后边没有标注带括号的公差，这是一个非常不厚道的标注（理论上没错），测量工程师和工艺工程师需要去查表，这是在浪费你同事的生命。

2）有效的传递配合信息

     这个也是最重要的。

     我们刚刚讨论过，就公称尺寸是Ø18的孔轴来说，为了达到滑配的效果，最小的间隙不能小于0.006， 最大的间隙不能大于0.035，只要能抓住这两点，就能满足“滑配”的效果。

     可是对于公称尺寸是Ø58的孔轴配合来说，还是控制最小间隙不小于0.006，最大间隙不大于0.035就可以了吗？

     或者公称尺寸是Ø100的孔轴来说，也是控制同样大小的最小间隙和最大间隙吗？

     显然不是，根据常识，同样的“滑配”效果，更大的公称尺寸需要的最大最小间隙会稍微多一点的，而更小的公称尺寸需要的最大最小间隙会更少一些。

     如何让不同公称直径的孔轴能配出来同样爽的“滑配”效果呢？

     显然孔轴必须采用同样的公差代号！

     事实上，不管孔轴的公称尺寸是多少，只要孔轴采用的公差分别是H7,g6(基孔制)，配出来的效果，就一定是滑配。

     也就是说如果孔轴配合如下图：

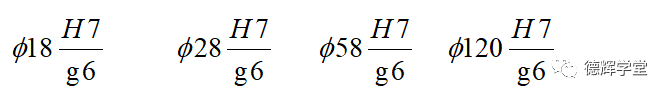
     他们配合的效果都是滑配。

     所以，机械前辈们搞出来的东西，对年轻工程师来讲，只要采用正确的配合，就能设计出满意的结构，而不需要去记住“间隙大概留多少”之类的局限性的知识。

     所以，采用公差代号来表达配合，它为经验知识的传承提供了一个很好的方法。

     问题又来了，实际上现在企业里很多工程师设计的图纸，几乎都抛弃了采用公差代号的标注方式，而直接采用数值公差。他们错了吗？

     我们不得不承认，采用公差代号是保证功能的一个方法，但并非唯一方法。用数值公差（非标准公差），也能设计出“滑配”效果。

     比如采用公差代号的滑配：

     我采用数值公差，也能配出同样的效果来：

     孔：

Ø18±0.009

     轴：

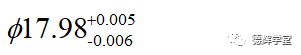
     上面奇葩怪异的设计中，最小的间隙是17.991-17.985=0.006， 最大的间隙是18.009-17.974=0.035，和Ø18H7/g6的效果是一样的！

     这样设计有错吗？除了看起来不舒服，对生产，对功能那完全没有问题。

     所谓，黑猫白猫，抓到老鼠就是好猫。

     但是，就配合而言，我还是比较推荐采用公差代号和标准里推荐的配合关系，那毕竟是机械前辈们留下来的东西，经过验证且是可靠的，不一定全部能满足我们的需求，至少有很大意义上的参照意义。

     但是如果走例外一个极端，非要按照标准公差来要求工程师出图纸，比如说工程师设计了一根轴，直径公差是:

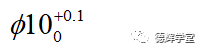
     就认为工程师的设计是错误的（标准公差里，没有0.1的公差），那也太教条主义了。毕竟，设计的逻辑是，在保证功能的前提下，零件能被加工，能被测量（控制）就行。

     好了，本期的文章就写到这里，希望对您有所启发。

本文小结

     本文就常见的公差和配合的基本知识做了介绍，属于大学课程《互换性与测量》的再回顾。

     第一章我们讲解了数值公差和公差代号的基本含义，详细解释了公差代号的三个基本量：公称尺寸，基本偏差，公差（公差等级），以及如何查表求得公差。

     第二章讲了三种配合，即间隙配合，过渡配合和过盈配合，讲了配合的表达，同时也解释了基孔制和基轴制的表达和特点，最后介绍了几种典型配合的应用工况。

     最后一章解释了采用公差代号和配合的意义。事实上采用公差代号就是为配合服务的，工程师合理的采用公差代号后，可以直接借鉴前辈们的经验成果。最后提了现在常用的数值公差也是保证功能的另外一个手段，公差代号并非唯一手段。

    希望本期文章对您有所帮助!

    觉得文章不错？点个赞呗，不想点？发个朋友圈也可以啊！

参考文献:

1. GB/T 1800.1-2009 极限与配合 第一部分：公差，偏差和配合的基础

2. GB/T 1801-2009  极限于配合 公差带于配合的选择

3. ASME B4.2-1978  Preferred Metric Limits and Fits

4. 互换性于测量技术基础 赵则祥 机械工业出版社