最新标准ASME Y14.5-2018发行后，我们发现它对基准偏移的章节增加了不少内容。这些增加的内容把基准要素的理想几何对配体（True Geometric counterpart），也就是以前老标准中的基准模拟体（Datum Simulator）的相关概念描述的更加详细。

     其中有一个章节，在新标准Y14.5-2018的107页， 图7-22中有个关于基准要素的MMB(最大实体边界)的计算解释：

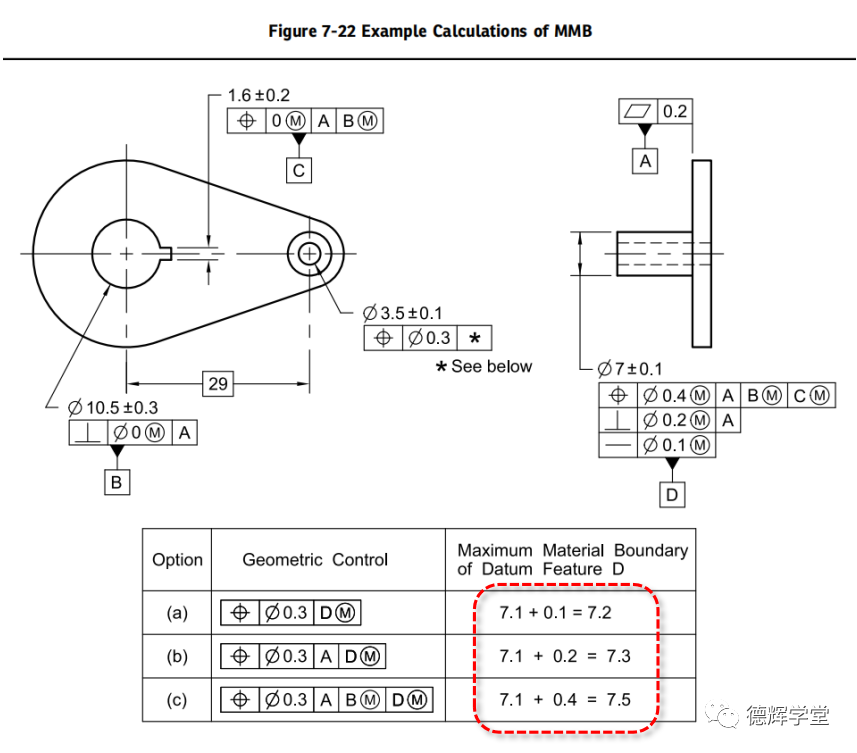
图1关于基准偏移的MMB

     很多小伙伴不太理解,MMB的大小为7.2，7.3，7.5的计算原理和依据是什么?

     还有，在标准的109页，图7-24中还给出一个基准采用RMB时的最大外边界MEB的计算解释，见图2.

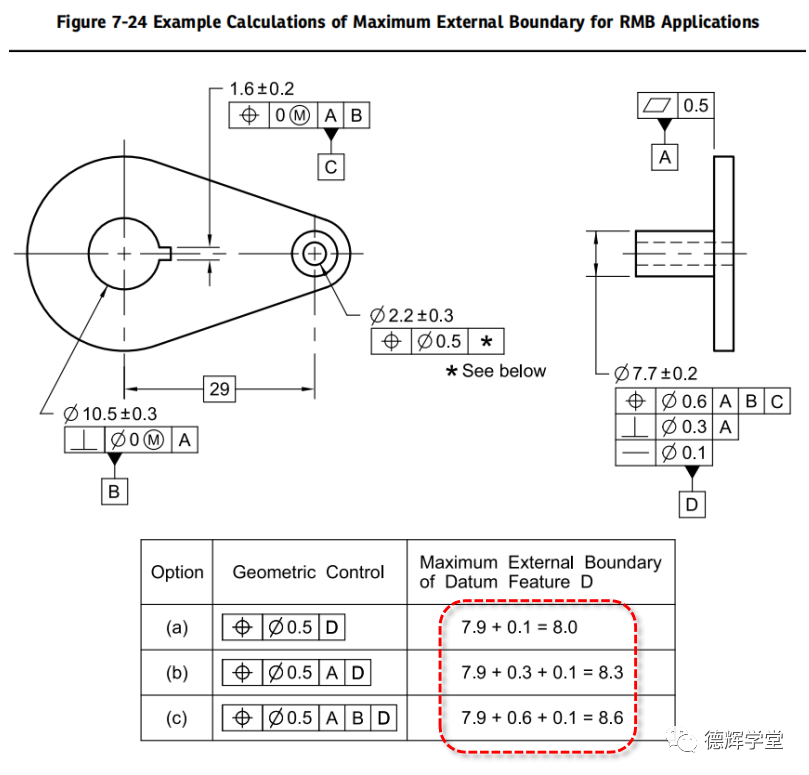
图2 基准采用RMB时的最大外边界的计算

     特别是图1和图2中对直线度Ø0.1的处理，图1只有在D作为第一基准时考虑，D作为第二和第三基准却不考虑。而图2中，第一，二，三基准中都考虑了直线度，这是为什么呢？很多小伙伴在这里纠结，甚至有小伙伴认为标准弄错了。今天我们就这个话题展开分析，好好来理一理，彻底把它搞清楚。

     本期文章的内容分为3部分：

1. 快速理解ASME标准中的边界理论

2. 采用MMC后的实效条件边界VC

3. 为什么MMB不考虑直线度

     为了照顾到基础相对薄弱的小伙伴，前两章的内容专门介绍了基础知识，对边界理论和实效条件边界VC已经非常熟悉的小伙伴，可以直接跳到第三章第二节。对基础知识相对不自信的小伙伴来说，建议静下心来，慢慢看完。

1. 快速理解ASME标准中的边界理论

1）边界的形成

      对于一个尺寸要素（FOS）来说，我们通常会标柱尺寸公差（比如直径）和几何公差（比如位置度）一起来控制。比如下面这个孔。

图3 用尺寸公差和几何公差控制孔

     而尺寸公差和几何公差之间，存在三种众所周知的关系，独立要求（RFS）, 最大实体要求（MMC）和最小实体要求（LMC）。

     熟悉ASME标准的小伙伴都知道，对于尺寸要素来说，垂直度，位置度控制的对象（公差带第五大要素）是非关联包容体（UAME）轴线，也就是孔的最大内切圆柱或轴的最小外接圆柱轴线。我们把图3中的被测孔剖开，再来认识一下UAME和它的轴线，见下图:

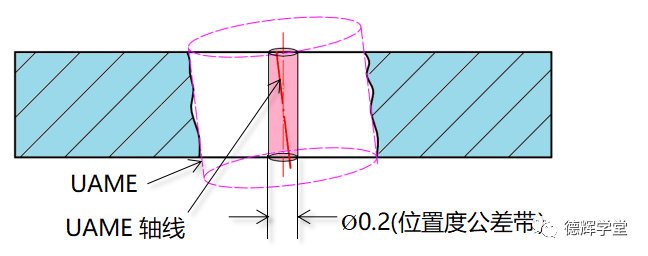
图4 非关联包容体和它的轴线

     图4显示的就是被测孔的非关联包容体（UAME）和它的轴线，位置度要求非关联包容体的轴线，必须在Ø0.2的公差带内。

    因为非关联包容体（UAME）的轴线可能在图4中Ø0.2的公差带内任何一个位置， 那么就会导致该孔在众多“可能”的位置中，形成极限的边界（Boundary）。边界有两种，内边界IB（Inner Boundary）和外边界OB(Outer Boundary), 见图5A, 图5B和图5C：

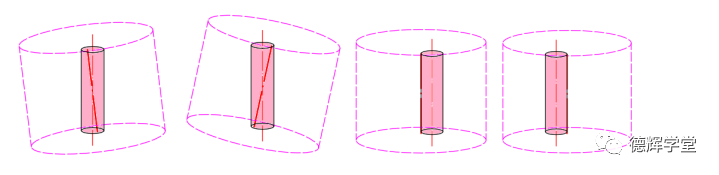
A 非关联包容体可能的位置

B 所有的可能性叠加

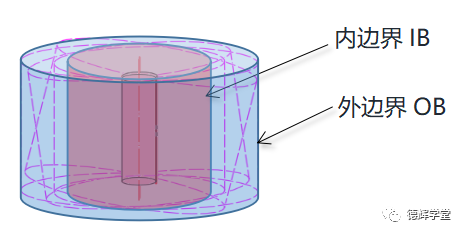
C 内边界IB和外边界OB

图5 内外边界的形成

     图5显示了内边界IB和外边界OB的形成。这个边界对设计和生产有着非常重要的指导意义，比如孔，用来装配的时候，设计工程师应该关心内边界，希望IB足够大，能够装的下轴；考虑最小壁厚的时候，设计工程师则应关心孔的外边界，希望OB足够的小，以保证最小壁厚，从而满足强度要求。这里不再详细赘述。

     对于内边界IB和外边界OB，保守起见，人们往往更加关心最坏情况，比如最小的内边界IB和最大的外边界OB。所以，在独立要求（RFS）时，边界的计算公式如下：

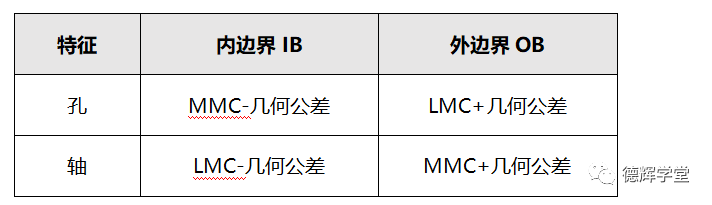
图6 孔轴内外边界的计算公式

     以上的内容在本公众号的《ISO边界之殇》中介绍过。有兴趣的小伙伴可以点击本文最后的链接。

2）三圆同心

     刚刚我们探讨了边界的形成，接下来我们再来看看内外边界的一个重要特点，那就是“三圆同心”。

B 公差带，内边界和外边界

图7三圆同心

     从图7中可以看出，被测孔在公差带里运动，会形成边界。其中内边界IB，外边界OB和公差带三个圆柱是绝对同心（或同轴）的，这种现象我们把它叫住“三圆同心”。

     三圆同心的这个心就是理论中心。

     因为三圆同心的这个特点，所以内边界IB， 外边界OB和公差带一样，和基准系保持理想的方位关系。

图8 内外边界和基准的关系

     如图8所示，外边界OB和内边界IB外形是一个圆柱，它们的轴线和基准A绝对垂直，而且和基准B的水平距离是绝对的16，上下距离是绝对的22。

     了解了边界理论的基本知识后，我们再来看ASME标准中的实效条件边界VC.

2. 采用MMC后的实效条件边界VC

     当尺寸要素的几何公差采用了最大实体要求（就是加M圈）后，见图9中红圈部分孔的位置度标柱。对这个位置度要求的解释，根据Y14.5-2018, 有两种解释方法：一个是轴线解释法（常规的三坐标测量就是用轴线解释法），另外一个是边界解释法（检具检测就是用边界解释）。

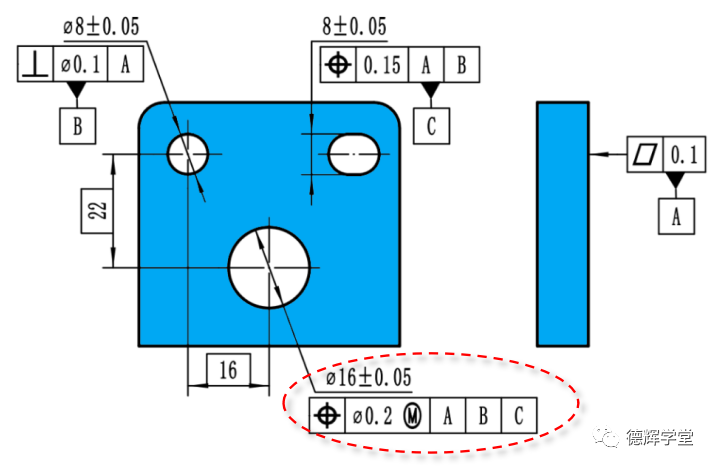
图9位置度采用最大实体要求

     这两种解释法，今天我们都有必来理一理。

1） 轴线解释法

     如果图9中，被测孔UAME的尺寸远离MMC， 就会产生补偿（Bonus）, 这个补偿会让几何公差的公差值变大。见图10和动图11：

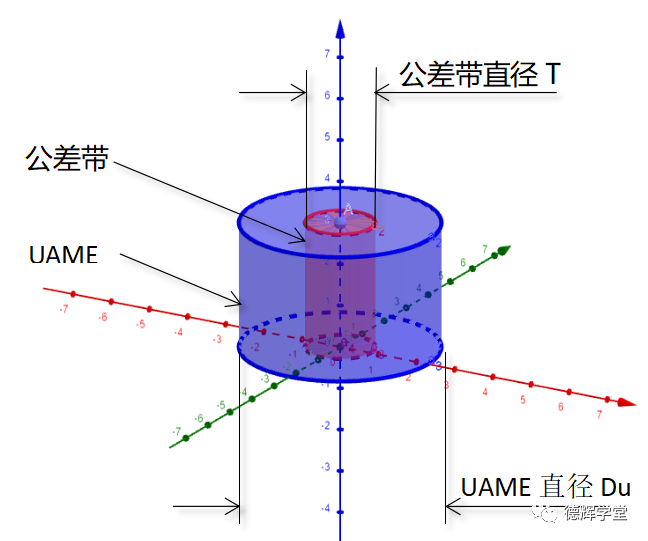
图10 UAME和公差带

     所以对孔来说，UAME越大，公差带就跟着变大，

     又因为补偿值的计算公式为：

Bonus = UAME - MMC

     所以从数值上看，UAME尺寸和允许的最大位置度公差存在下面的关系：

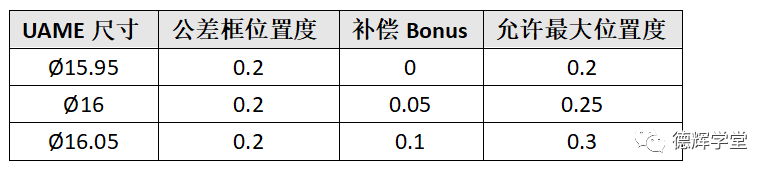
图12 UAME尺寸和最大位置度

     只要UAME的轴线，不超出图12中的允许最大位置度，该孔的位置度就是合格的。

     这就是轴线解释法。

     对最大实体要求补偿的游戏规则还不熟悉的小伙伴，应该对它的游戏规则记得滚瓜烂熟才行。

     我们再来看看基于轴线解释法，对边界的影响是什么。

     结合第一章节图6中提到的边界计算公式，我们就可以计算当采用最大实体要求后的内外边界了。从而可以观察，采用最大实体要求后对内外边界的影响。

图13 最大实体要求和内外边界的关系

     仔细观察图13中的数据，我们发现采用最大实体要求后，尽管有了补偿，允许的位置度不断变大，但是对内边界IB却没有影响。

     这个固定不变的内边界（直径为Ø15.75），就是我们今天要重点讨论的VC，实效条件边界（有时候也叫实效边界）。在ISO标准中，也就是我们常常提到的MMVB（最大实体实效边界）。

     注意，孔的VC就是内边界，轴的VC就是外边界。它是一个圆柱形的空间，它的计算公式如下：

图14 VC的计算公式

     我们再用动图来理解，尽管孔的UAME尺寸和允许的位置度都在发生变化，但是孔的内边界不会变得更差。

图15 采用MMC后的内边界不变

     这个VC对我们也有非常重要的意义，比如用在装配孔时，判断一根轴能否顺利穿过这个装配孔而不发生干涉，完全是看这个孔的VC是否能全部容纳这根轴。

     2）边界解释法

     我们再来看看边界解释法。

     ASME的边界解释法其实本质和ISO2692一样，非常蛮横。它就一个解释，如果一个尺寸要素采用了最大实体要求，它的VC边界就不能被侵犯。

     什么意思呢？

     比如一个孔采用了最大实体要求（加M圈）后，它就会有一个实效条件边界VC存在，根据图14中的计算公式，这个VC的大小为：

VC = MMC -几何公差

     VC的形状是一个理想的圆柱。这个VC就是一个神圣的国际边界线，被测孔圆柱面上的任何点，都不能跨过这个VC边界。

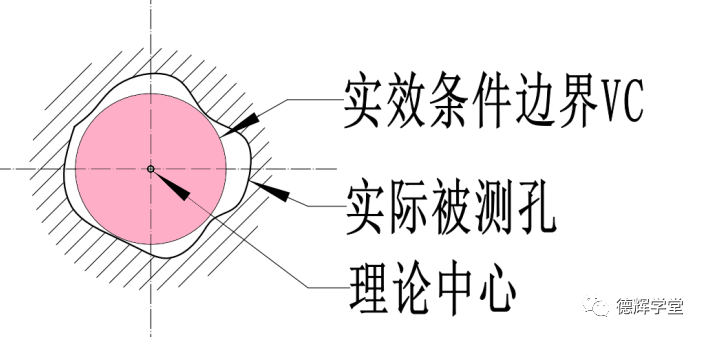
图16 不能跨越的VC

     如图16所示，边界解释法的意思是，实际被测孔上的任何一点，都不能进入粉红色的VC以内（允许刚好在边界上）。

     这个边界解释法，对现实的指导意义在于，如果一个孔的几何公差采用了最大实体要求后，为了检测孔的几何公差，我们做一个检测销（图16中粉红色的圆）来模拟这个VC，检测销的直径就做成VC的直径（Ø15.75），如果检测销能够顺利的通过被测孔，那么就能证明被测孔没有侵犯VC的空间，即几何公差满足要求（当然，这是以尺寸公差首先满足要求为前提）。

     反过来，只要实际被测孔圆周上任意一点跨过了VC边界，检测销肯定不能完全插入，则被测孔就不合格。

     凭着我们的直觉，是不是感觉边界解释法和装配很相似？

     我们再继续深入。

     有没有一种情况，轴线解释和边界解释不一致呢？比如说，轴线解释是不合格的，而边界解释是合格的？

     真有这种情况。

    假设有一个被测孔，它的几何公差采用了MMC， 它的UAME轴线（就是UAME中心）和VC边界的状态如下图所示：

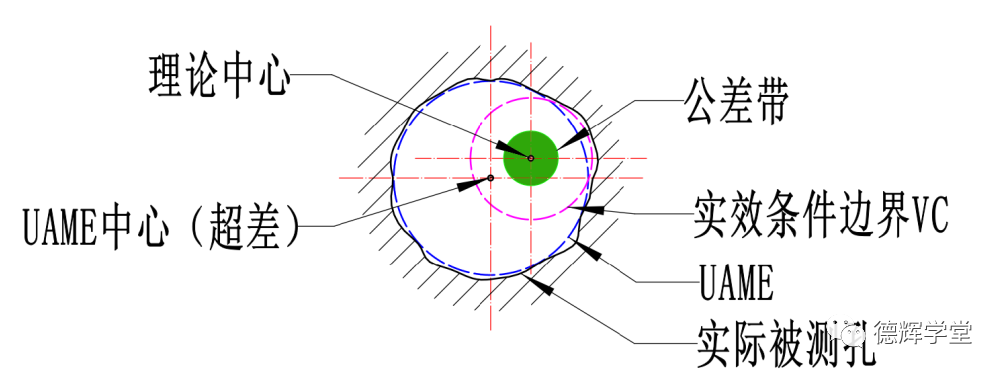
图17 轴线解释和边界解释不一致

     图17中，在实际被测孔的尺寸合格的前提下，UAME（见蓝色的最大内切圆）的中心轴线刚好在公差带（已经考虑补偿后）以外，按照轴线解释，这是超差的。

     可是如果我们再仔细观察该孔内部的实效条件边界VC（紫色虚线圆），发现这个VC边界却没有被侵犯，所以按照边界解释，它是合格的。

     这下好了，矛盾出现了。

     图17在现实中的体现是，用三坐标测量被测孔，发现它的位置度是超差的（三坐标按照规范的方法测量），但是用检具去测量，却发现它是合格的。

     遇到这种情况，究竟听谁的呢？

     根据Y14.5-2018中的规定，如果轴线解释和边界解释发生冲突时，以边界解释为准。这种规定，我把它称为“边界优先”原则。

     就是因为边界优先原则，所以当三坐标检测结果和检具检测结果发生冲突时，听检具的。

     可是，ASME为什么要规定边界优先呢？

     这一点，ASME标准没有给出明确的解释，看起来比较蛮横。但是我们是可以揣测ASME标准背后的逻辑的，很简单，那就是: 管他呢，能用就行。

     稍微再扯一句， ISO2692中，甚至都没有给出轴线解释的规范（所以ISO标准连补偿Bonus的概念都没有），也是用边界来解释的：在尺寸合格的前提下，不管你怎么作，MMVB（最大实体实效边界）不能被侵犯。

     ISO标准的潜台词也是，管他呢，能用就行。

     两个标准尽管平时相互看不起，但在耍流氓这一点上，倒是十分臭味相投。

     我们再回来，“边界优先”是我们理解ASME标准中关于MMB大小的关键，第三章我们会详细讨论。

     注意，“边界优先”，也就是VC优先，这个规定只对MMC和LMC适用，即采用了相关原则适用，对独立要求RFS不适用。  

     到这里，我们对采用最大实体要求后会形成一个实效条件边界VC，做一个小小的总结。

     1. 对孔来说，只要它的几何公差采用了最大实体要求，就一定存在一个实效条件边界VC。它也是孔的内边界IB，在实际被测孔的内部：

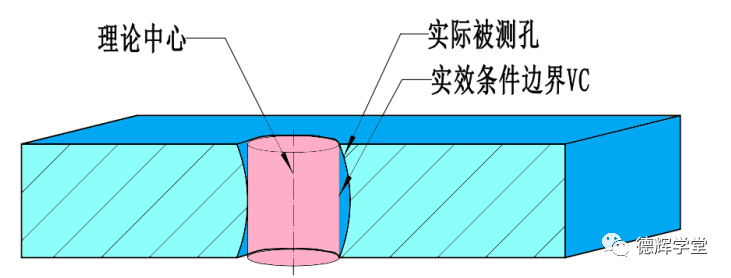
图18 孔的实效条件边界VC

     对轴来说，只要它的几何公差采用了最大实体要求，就一定存在一个实效条件边界VC。它是轴的外边界OB，在实际被测轴的外部。

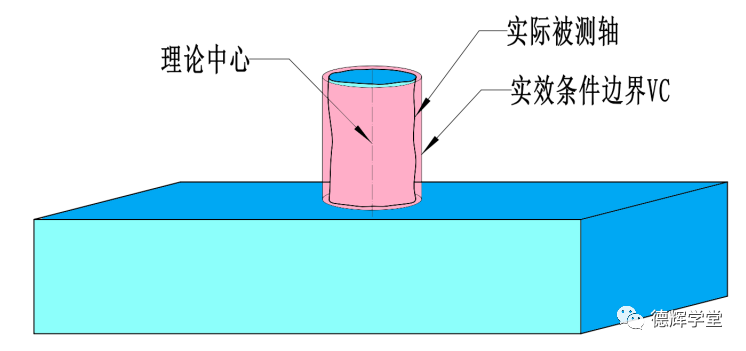
图19轴的实效条件边界VC

     而且，基于三圆同心，图18和图19中的VC，它们和基准系保持理想的方向关系和位置关系。

3. 为什么MMB不考虑直线度？

     在开始讨论本期文章的主题之前，我们首先要弄清楚是什么是MMB, 再回到本期章开头的内容，讨论MMB为什么不考虑直线度。

1）什么是MMB

     MMB（Maximum Material Boundary）其实就是指对基准要素采用了最大实体要求，图纸上的体现就是基准后边加M圈。

     它本意是说，基准的建立（基准要素和基准模拟体的贴合）是在当基准要素处于最大实体边界时建立的，也就是当基准要素占用体外空间最多的时候建立的。

     MMB同时也是一个边界，当基准要素占用体外空间最多的时候（注意，是占用体外空间最多的时候），此时，用一个反形体去“贴合”该占用体外空间最多的基准要素，贴合好后，这个反形体就是基准模拟体（Datum Simulator）, 新标准Y14.5-2018把这个反形体叫做“理想几何对配体”（True Geometric Counterpart）。

     MMB的特点是，它的大小就是最大的基准模拟体的大小。

     我们说人话呢，这个理想几何对配体，就是检具上代表基准的定位孔，定位销了。

     因为基准要素占用体外空间最多时的状态是极限状态，极限状态的边界是唯一的，所以基准模拟体的大小就是唯一的固定值（也就是说，检具上的定位孔，定位销的直径是固定），不像RMB（基准没有任何修饰符号），基准模拟体的大小随着基准要素的状态变化而变化。

     如果现实中的基准要素不处于极限状态怎么办？（其实，绝大部分情况都不处于极限状态），那就表示基准模拟体（或定位孔和定位销）和基准要素之间有间隙了，这个间隙就允许零件和检具之间可以浮动，可以找补偿，这个浮动就是基准偏移（Datum Shift）。本公众号我们探讨过相关的内容，有兴趣的小伙伴可以点击文章最后的链接。

     当然，既然是基准模拟体，根据基准系建立的法则，基准模拟体必须要和它的高序基准保持理想的方位关系（第一基准的基准模拟体因为没有比它更牛逼的高序基准，所以除外）。

     废话少说，上一个图举例说明吧。

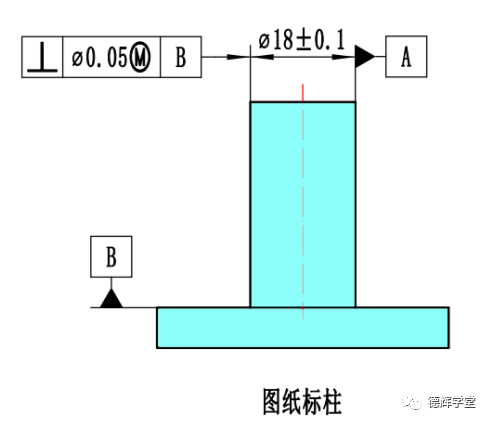
图20 图纸标柱和实际零件

     我们以基准A作为研究对象，来理解一下什么是MMB。

     首先如果几何公差是以A作为第一基准见图21，A的基准模拟体，就是用一个圆柱形的圆筒（和基准要素相反的反形体）去“包容”实际轴，刚刚好包住后，这个圆筒就是基准模拟体。因为是第一基准，显然这个圆筒也是非关联包容体（最小外接圆柱）。见下图：

图21 第一基准的MMB

     因为基准加了M圈，基准模拟体就有一个固定边界，即MMB。根据MMB的定义，MMB就是指基准要素占用的最大的体外空间时的边界，也就是图21中UAME最大的时候。

     UAME最大是多大呢？

     因为ASME标准默认包容原则，包容原则除了要求尺寸要素的两点尺寸必须满足要求外，还要求UAME尺寸也必须在尺寸公差范围内，也就是说，UAME最大最大也就是MMC了。

     所以对于第一基准来说：

MMB = UAME_max = MMC = Ø18.1

     如果我们在检具上挖一个代表A基准的定位孔，即现实版的基准模拟体，或现实版的MMB，该定位孔的直径是Ø18.1。

     我们再来看看A作为第二基准时的基准模拟体，见下图：

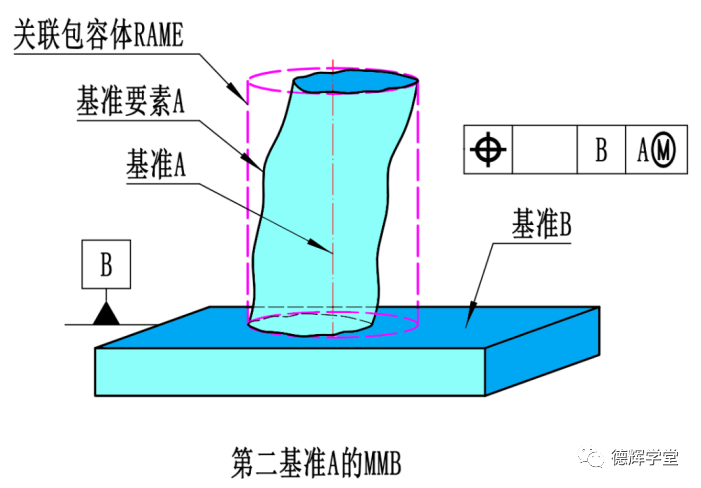
图22 第二基准的MMB

     作为第二基准的基准模拟体，因为它必须要和第一基准（高序基准）保持理想的方位关系，即它要和第一基准B绝对垂直，在这种前提下，基准模拟体对应的几何体不再是非关联包容体UAME了，而是关联包容体RAME。所谓关联包容体，就是一个几何体，它必须和基准A保持绝对垂直的关系为前提，再去包容基准要素。

     那么最大的基准模拟体，也就是图22中最大的关联包容体RAME，是多少呢？

     这个显然和A相对于B的垂直度有关系，结合第一章和第二章的内容，图22中的最大关联包容体，就是A的最大实体条件边界VC。

     显然有，

MMB = RAMEmax = VC = MMC +垂直度 

          = 18.1 + 0.05 = Ø18.15

     稍微再强调一下，这里的MMB可以计算出来是Ø18.15，完全是因为图23中垂直度的原因，因为根据“边界优先”的原则，Ø18的轴要想满足垂直度的要求，轴表面上所有的点必须在直径为Ø18.15的边界（VC）以内，所以基准要素A（Ø18的轴）能够相对于B占用的最大空间不会超过Ø18.15。

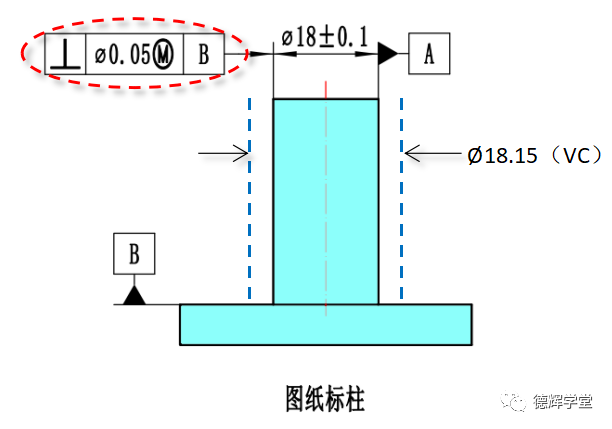
图23 垂直度和边界优先

     好了，做了长长的铺垫后，我们再来分析本文开头提出的问题，ASME Y14.5-2018中关于MMB的计算。

2）MMB要考虑直线度吗？

先直接看图吧。

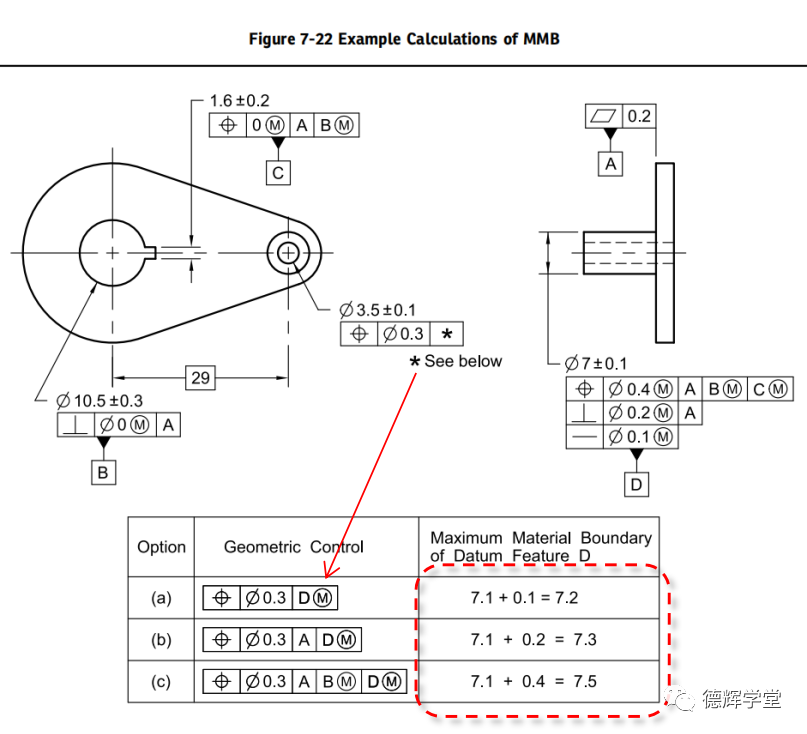
图24 ASME标准中关于MMB的计算

     图24中，D是一个直径为Ø7的轴，然后分别用以它作为第一基准，第二基准，第三基准的位置度去控制Ø3.5的孔。

     而这个基准要素D，本身又被位置度，垂直度，直线度控制。

     我们接下来一行一行分析。

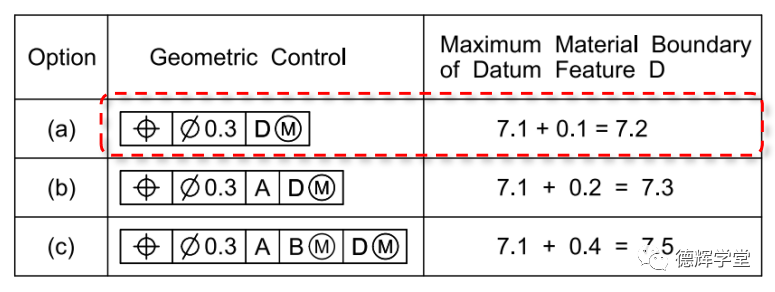
图25 第一行的MMB

     第一行的位置度中，基准D作为第一基准，显然根据我们前面的分析，D的MMB，就是最大的UAME了（作为第一基准，基准模拟体不需要和任何基准关联，因为它就是老大）。

     最大的UAME是多大呢？

     我们前面讲的案例中，UAME就是MMC，那是因为在包容原则的约束下，UAME不可能超出MMC。

     但是在图24中，因为有直线度的原因，包容原则是失效的（这是包容原则的失效情形之一），所以MMC不能约束UAME的直径了。又因为，直线度采用了最大实体要求（M圈），所以直线度和尺寸公差会形成一个最大实体条件边界VC。根据VC的计算公式有：

VC = MMC+几何公差 = 7.1 + 0.1 = 7.2

     见下图：

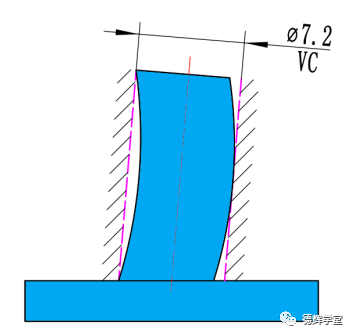
图26 第一行的MMB图解

     注意图26中的VC是尺寸和直线度共同作用的实效边界，不需要和任何基准保持关系。所以根据边界优先原则，因为直线度的原因，作为第一基准的D，能够侵占的最大空间一定不会超出图26中的VC边界，最多也就是刚好达到VC边界。即可以得出：

MMB = UAMEmax = VC =7.2。

     第一行得证。

     我们再来看第二行：

图27 第二行的MMB

     第二行的D基准是作为第二基准，所以我们关心它相对于A的最大实体边界(它其实是一个关联包容体)。显然我们这个时候就要考虑第二行的垂直度了，因为垂直度会影响这个边界。

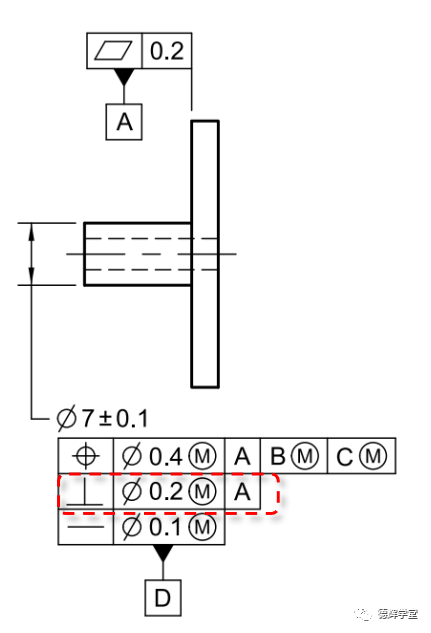
图25 必须考虑第二行垂直度

     第二行是被很多小伙伴纠结过的地方，主要原因在于，既然D的非关联包容体的直径可以达到7.2（见图26A），它如果再倾斜0.2（见图26B），那它相对于A的关联包容体不就是7.2+0.2=7.4了么？见图26C：

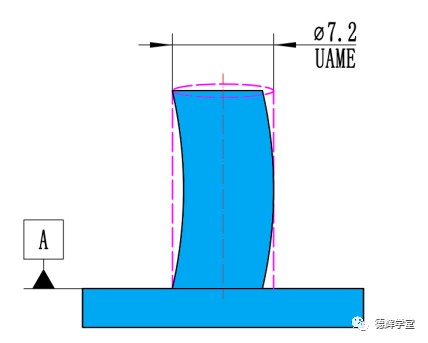
A. 刚开始垂直度理想

B. 倾斜到垂直度为0.2

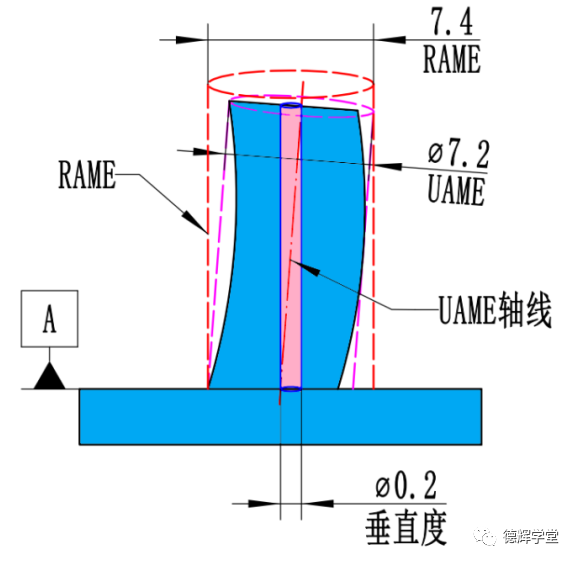
C. 关联包容体RAME是7.4

图26 关联包容体的尺寸误解

     如图26所示，如果基准要素D相对于A的最大关联包容体RAMEmax=7.4, 那么根据前面讲的逻辑，我们则可以推演出：

MMB = RAMEmax = 7.4

     而ASME标准中明明写的是基准要素D的MMB=7.3.

     ASME标准弄错了吗？

     答案是，标准没有弄错，作为第二基准，基准要素D的MMB应该是7.3。

     为什么呢？

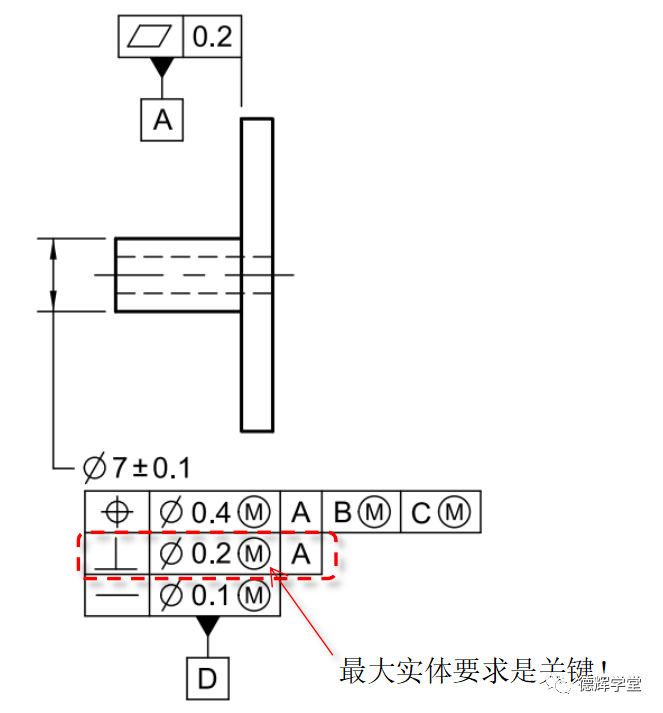
图27 关键的MMC

     大家还记得我们前面讨论的“边界优先”原则吗？

     见图27，因为垂直度带最大实体要求，就意味着有一个边界VC存在，这个VC和基准A绝对垂直，而Ø7的轴无论如何折腾，是不能超出这个VC边界的（这是垂直度的要求），不管它是独立原则，还是有其它任何要求。

     所以因为垂直度采用MMC ，显然有:

VC = MMC + 垂直度 = 7.1+0.2 = 7.3

     见下图28：

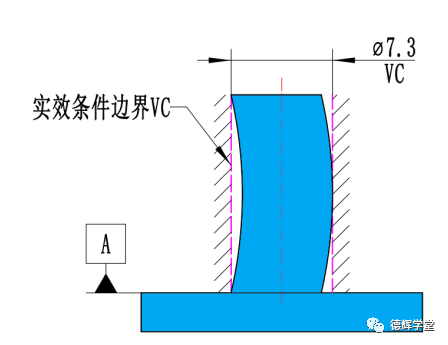
图28 垂直度的实效边界

     所以因为垂直度的要求，就导致基准要素D相对基准A的关联包容体一定不会超过VC，最多刚好达到VC，即：

MMB = RAMEmax = VC = Ø7.3

     有小伙伴可能不服气了，不对啊，为什么不考虑直线度的影响呢？

     不需要的，在GD&T里边，如果用多行组合公差标柱的话，那就意味着被测要素每行都必须满足要求才算合格。也就是说尽管有了直线度的要求，并不意味着垂直度要求（遵循边界优先）就允许被破坏。

     也就是说，基准要素D既要满足直线度要求，又要满足垂直度要求，这是一个交集的逻辑关系，不是并集。

     到这里，大家明白为什么D的MMB是Ø7.3而不是Ø7.4了吧。

     基于同样的逻辑，我们来看第三行，就非常容易。不难算出作为第三基准的MMB:

MMB = RAMEmax = VC = MMC + 位置度 

          = 7.1 + 0.4 = 7.5

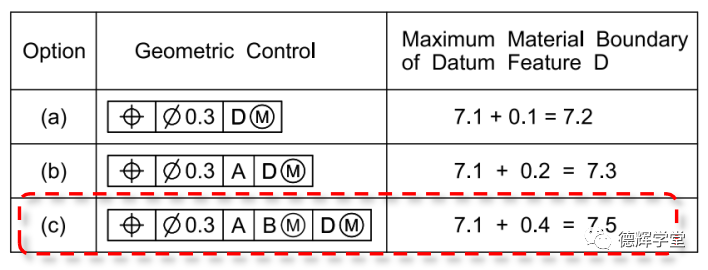
图29 第三行的MMB

     我们再回过头来重新分析D基准的MMB，分析它的关键点在于分析基准要素自身的特点，它在作为被测要素时，由于采用了MMC（最大实体要求），，它必循遵循VC边界（边界优先），不能逾越。所以才导致它作为基准要素时，其最大实体边界MMB最多也就刚好达到VC。

     那么我们再问，如果基准要素在作为被测要素时，没有采用MMC，那么它的最大边界需要考虑直线度吗？比如下图：

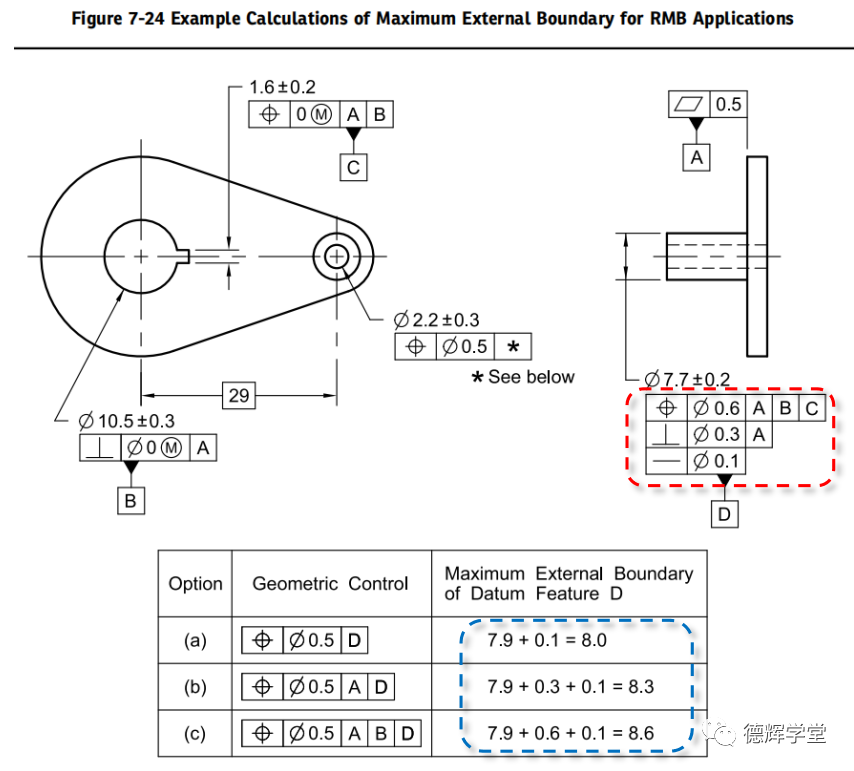
图30 被测要素D没有采用最大实体要求

     如图30中红框部分，D作为被测要素时，因为采用的是RFS要求（独立要求），不需要遵循边界优先原则（它没有VC，只有IB和OB），这个时候的分析方法就必须按照图26的思路来分析。

     所以算出来基准D的最大外部边界（Maximum External Boundary）见图30中的蓝框部分，稍微提一下，因为基准没有加M圈，所以没有MMB这个概念，只有最大外边界MEB这个概念。

     这里快速过一下：

     分析思路是，因为有直线度，所以不需要遵循包容原则，图30中的D的UAME最大可以达到：

UAMEmax = OB = MMC + 0.1 = 7.9+0.1 =Ø8.0

     这个就是第一行，作为第一基准时，基准要素D的最大外部边界。

     我们来看看D作为第二基准时的最大外部边界：

     因为垂直度控制的对象就是UAME的轴线，所以如果这个UAME（其最大直径为Ø8.0）的轴线再倾斜0.3（垂直度），那么相对于A的最大关联包容体为：

RAMEmax = OB = UAMEmax + 垂直度 

                = 8.0+0.3 = 8.3

     这个就是第二行的，作为第二基准时，基准要素D的最大外部边界。

     同样，看看最后D作为第三基准时的最大外边界，基于同样的逻辑有：

RAMEmax = OB = UAMEmax + 位置度 

               = 8.0 + 0.6 = 8.6

     好了，终于讲完了。

     这就是本期文章的全部内容，希望对您有所帮助。

本文小结

     本期文章对ASME标准中，关于基准偏移部分有争议的地方做了解释。为了照顾到基础比较薄弱的小伙伴，本文分为三个部分来阐述：

     第一个章节讲了ASME标准中，尺寸要素边界的形成，它是尺寸公差和几何公差综合作用的结果，并且列出了孔轴内外边界的计算公式。

     第二个章节讲了最大实效条件边界VC，指出如果孔轴加了最大实体要求（MMC）后，会形成一个最大实效边界VC。并且强调，如果几何公差采用MMC后，用两种解释方法，一种是轴线解释，一种是边界解释，当两种解释发生冲突的时候，那么边界优先。其中，边界优先是解决本期问题的关键点。

    第三个章节讲了MMB的概念以及算法，解释了D基准的MMB为什么不考虑直线度，主要原因是D基准要素作为被测要素时，因为它采用了MMC要求，它就必须遵循边界优先的原则，不能超出VC，这就决定了MMB的大小， 所以第二行和第三行，直线度是影响不到MMB的。同时也讲解了基准要素作为被测要素时，如果采用了RFS， 直线度会影响MMB的。

【后记】

     写本期文章的之前，很多工程师和老师都和我一起讨论过这个问题，ASME标准在这里的描述特别令人费解，它也没有做更多解释。

     作为一个技术观点的讨论，我将我的理解发出来，供大家参考，欢迎有不同意见的小伙伴在留言区发表不同的看法。

觉得文章不错？点个赞呗，不想点？发个朋友圈也行啊。