在做结构设计的时候，设计者往往会采用一面两销配上一面两孔，这是一种非常常见的定位结构，它能够有效限制零件的6个自由度。

而为了追求更高的定位精度和更低的经济成本，一个圆孔（主定位部分）加上一个长腰孔（副定位部分），在现在的定位结构中更容易被工程师们采用，它也能有效限制零件的6个自由度。比如下图：

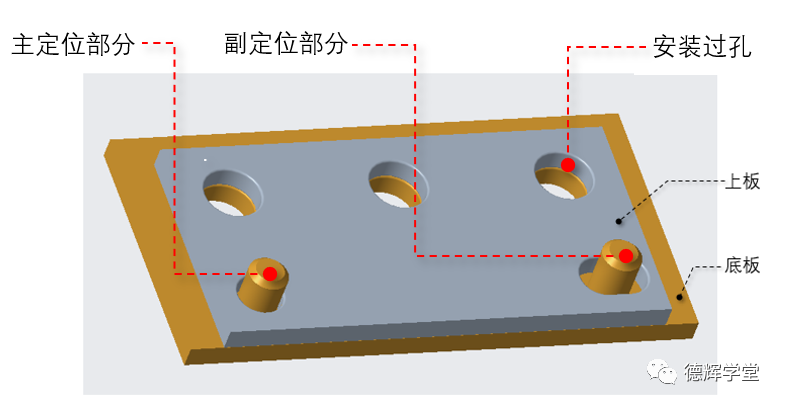
图1 一面两销和一面两孔

图1中，黄色底板用一面两销，而灰色的上板就是一面，一圆孔加一个长腰孔。这种结构在零件相互之间装配定位，或者在钣金件的焊接定位工装上经常被采用（比如汽车的副车架定位）。

动画1 上板和底板的定位

当工程师在设计这种“一面两销和一面两孔”时，为了方便装配操作，往往会在销孔之间留有少量的间隙δ，比如下图：

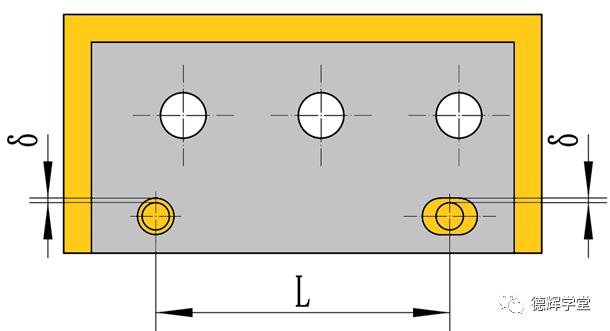
图2 销孔之间留有小间隙δ

就是因为这个不得不留的小间隙δ的存在，会给装配件之间的定位精度带来负面影响。比如，会让图1中的上板相对于底板发生随机的“浮动”，见下面动画：

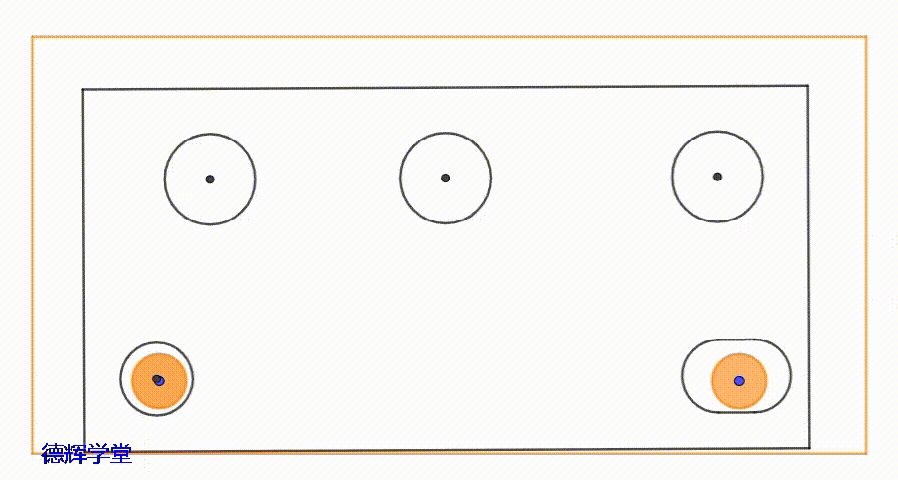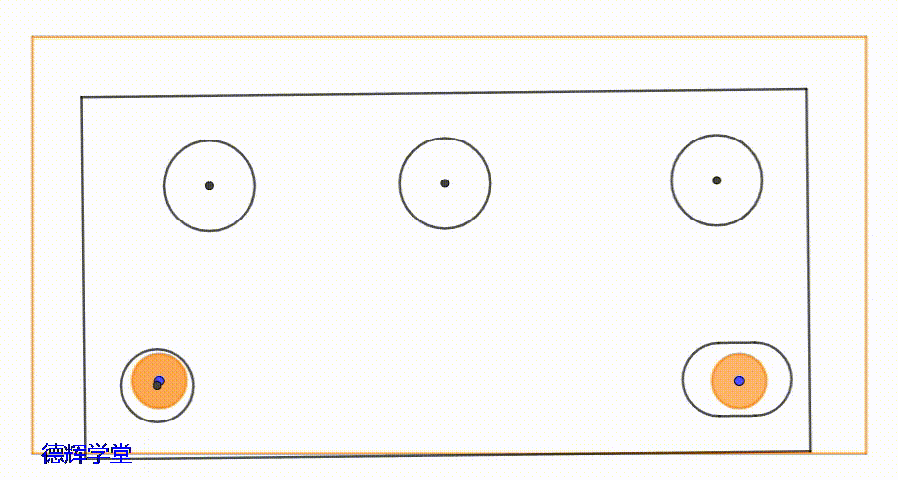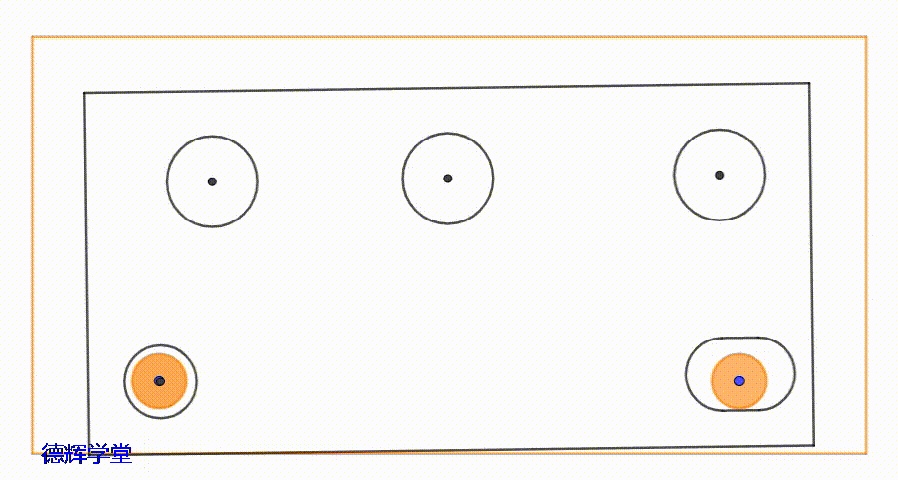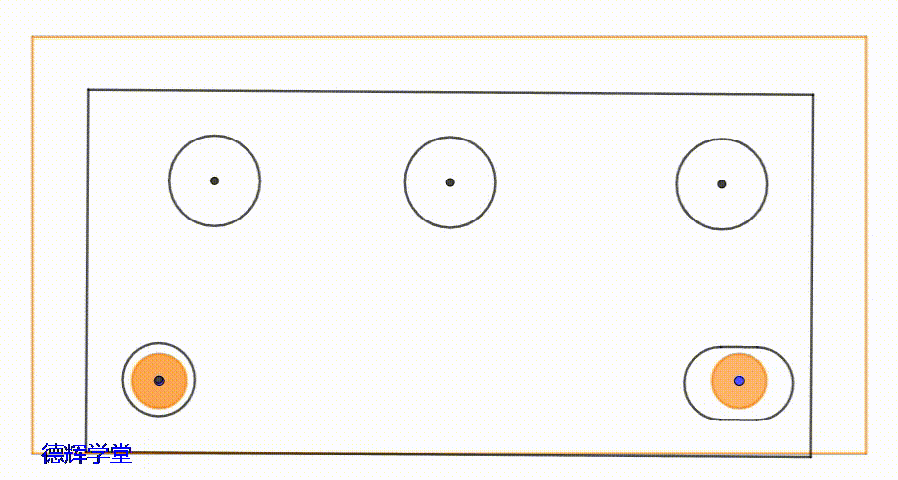
动画2 两零件间的随机浮动

我们先假定图1中，两个零件定位好后，会被点焊固定。那么动画2中的随机浮动，无法被还原和复位，它对装配是有害的。

因为，它会让底板的3个安装孔，上板的3个安装孔，相互之间会发生“错位”的现象，导致两个零件的安装孔相互之间的“公共有效空间”会变小。

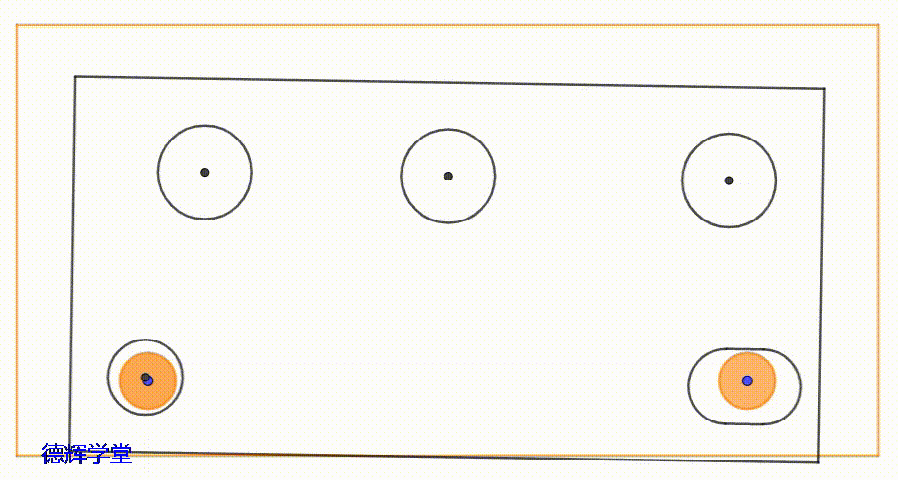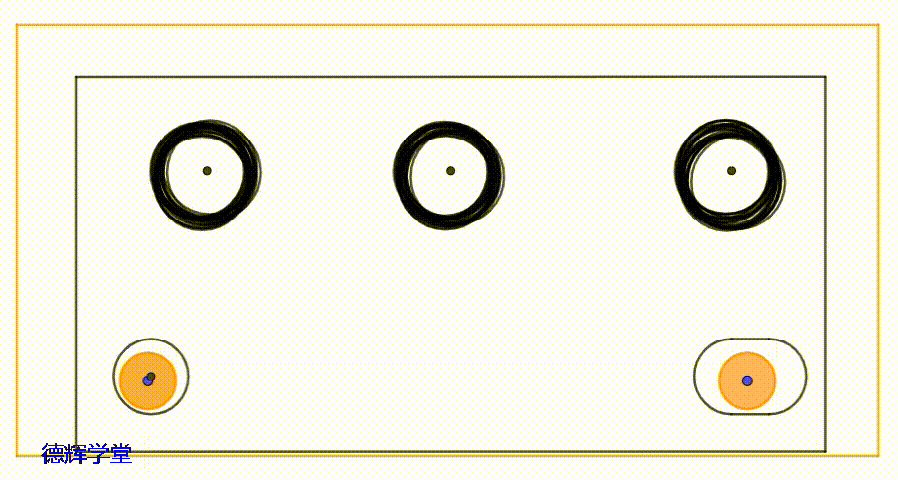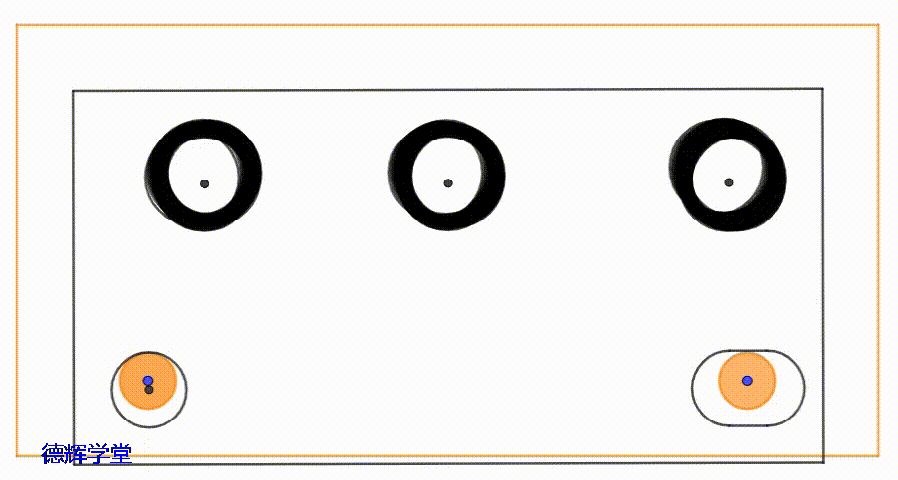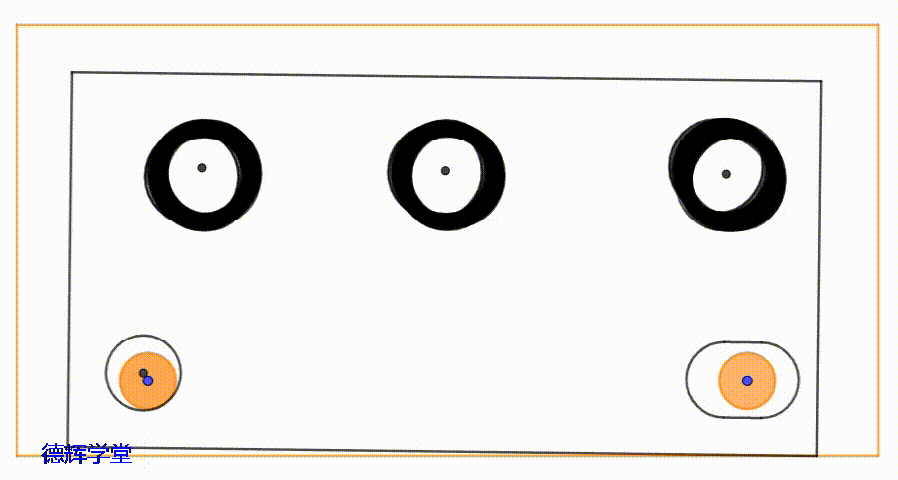
动画3 安装孔的运动轨迹

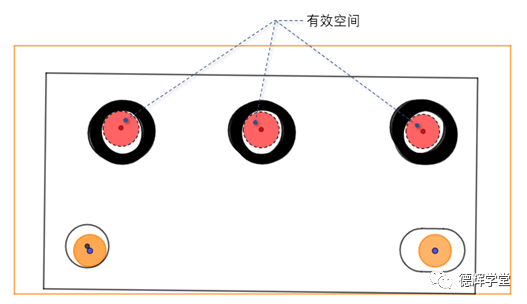
图3 变小的有效空间

见图3，红色的3个圆，就是在发生孔销浮动后，留下的空芯空间，这个空间才是可以用来穿螺栓或销子的“有效空间”。

不管怎样，就是因为孔销浮动，导致实际有用的有效空间（图3中红色的圆）比过孔自身的直径还要小。

所以，当孔销浮动发生后，工程师们更加关心的是，有效空间是多少？或者说，上板安装孔的中心相对于底板安装孔的中心偏了多少（工艺工程师们更加关心这个）？

本篇文章我们就一起来探讨这个问题。还是老套路，本期文章将分3个章节：

因为篇幅较长，本期文章我们只放送前面两章，最后一个章节我们下一期放送。

本期文章参考了国外学者撰写的相关论文，可能数学味道比较重，大家要有思想准备。但是，我们会结合大量动画和图例，尽量把其中的关系给大家讲清楚。

另外，本期文章主要集中探讨纯粹的孔销浮动，形位公差先不讨论。所以本期文章的假设前提是，每个零件都是刚性理想的。（最终形位公差带来的影响一定要讨论，下一期文章我们会讨论如何嵌入形位公差来综合分析）

在开始讨论之前，我们首先要在装配图中建立两个坐标系（见图4）。一个坐标系是XYZ（蓝色）是建立在黄色底板上,因为底板是不动的，所以我们把XYZ叫母坐标系（或全局坐标系），另外一个坐标系是xyz（红色）, 是建立在灰色的上板上的，叫子坐标系（或者局部坐标系）。见下图：

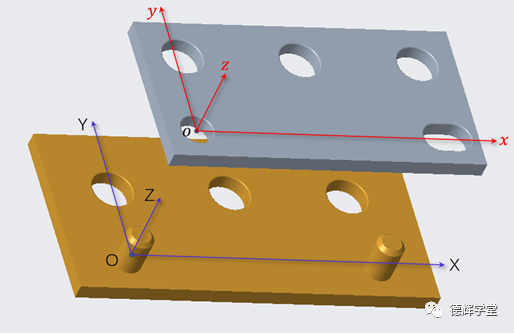
图4 两个坐标系

图4中的两个坐标系，我们后边会用到（因为零件比较薄，我们会主要用到2维的坐标系XOY和xoy）。

注意，本篇文章对研究基准偏移来说非常重要，对定位精度的研究也非常重要，希望在您耐心看文本期文章后，对您有所启发。

1.    孔销浮动的现象

     本章节我们先来直观的认识一下孔销浮动。

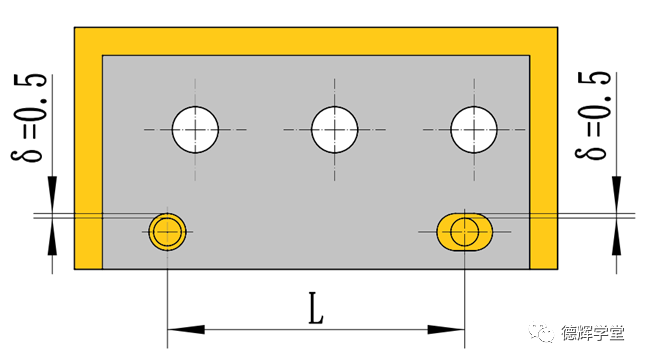
图5 销孔单边间隙是0.5

见图5，我们先假定主副定位销孔之间的单边间隙都是0.5，这样上板和下板之间就会发生随机的孔销浮动。

孔销浮动主要来源于两个，一个是来自于主定位部分的孔销浮动，一个是来自于副定位部分的孔销浮动。

当然，其他特征（比如3个安装孔）会因为定位部分的孔销浮动，被动地“浮动”。

我们一个一个来感受。

1）主定位部分的孔销浮动

    主定位部分的孔销浮动比较简单，就是一个圆孔相对于一个圆销的随机浮动。

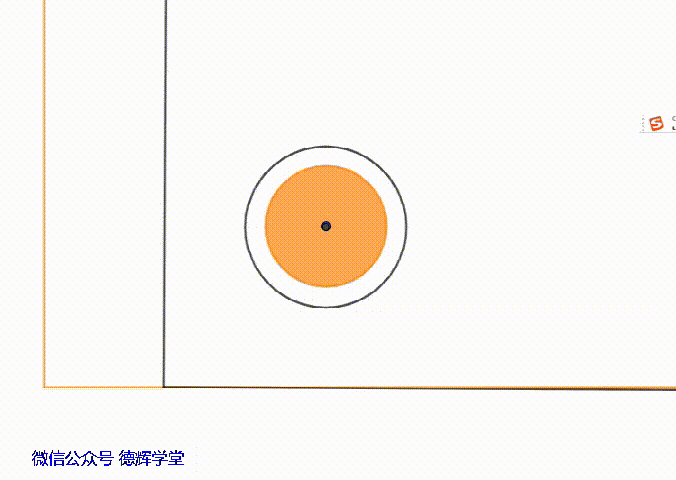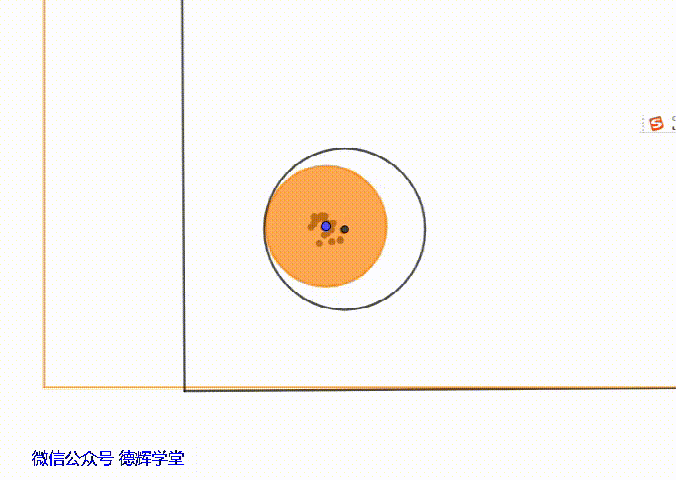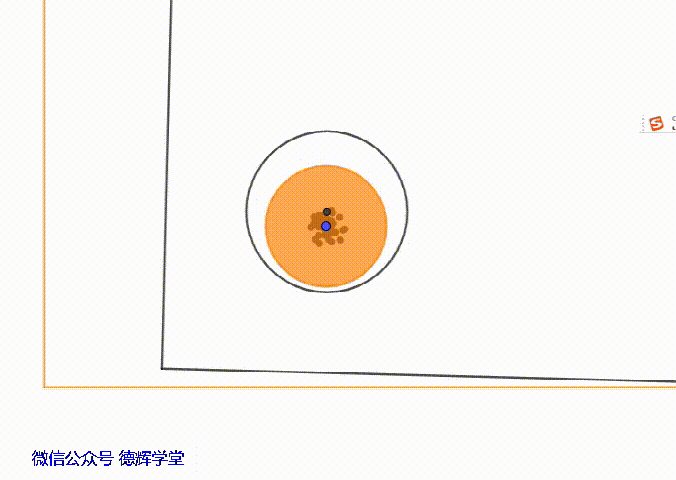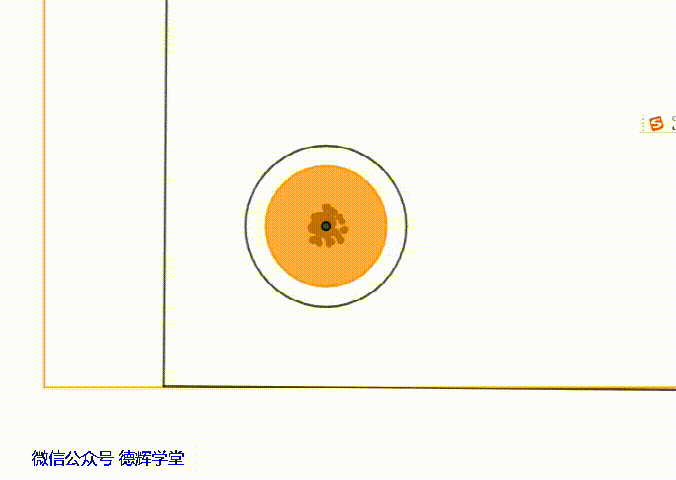
动画4 主定位孔相对于主定位销的浮动

动画4中，黄色的底板不动，上板在浮动。如果我们仔细观察上板主定位孔的中心，就会发现，该圆孔中心的浮动范围其实是在一个小圆内，这个小圆的半径就是单边间隙δ。

在极限的位置，就相当于主定位孔的中心，可以在一个小圆的圆周上游走。刚刚提到过，这个小圆的的半径就是单边间隙δ，也就是0.5。

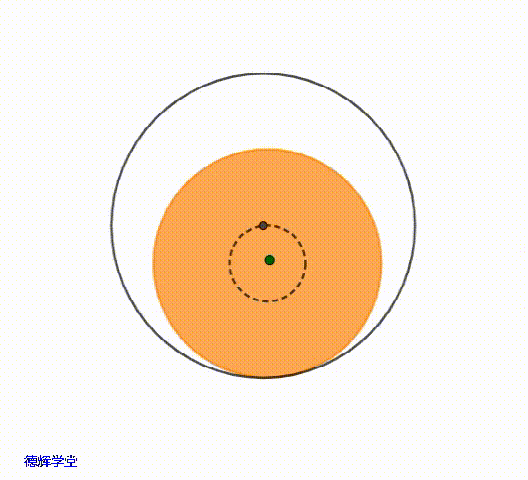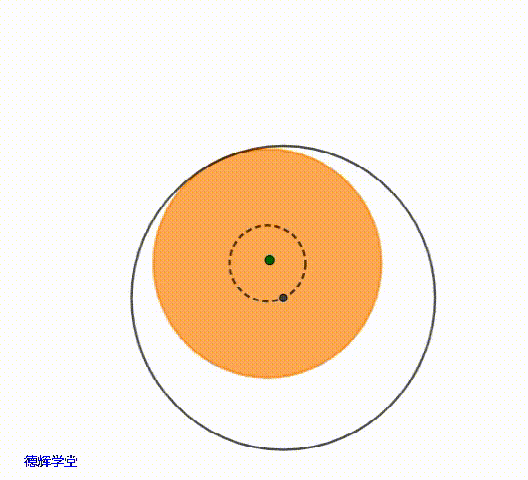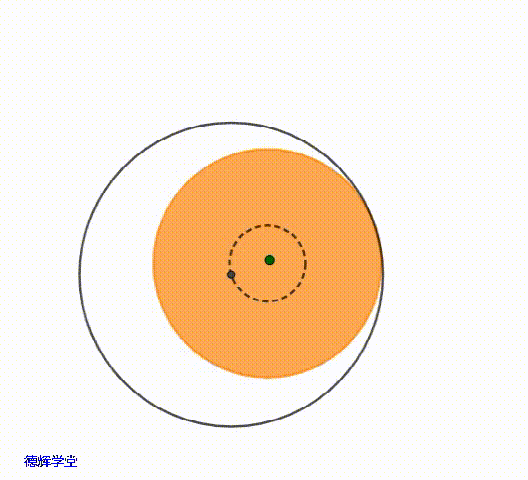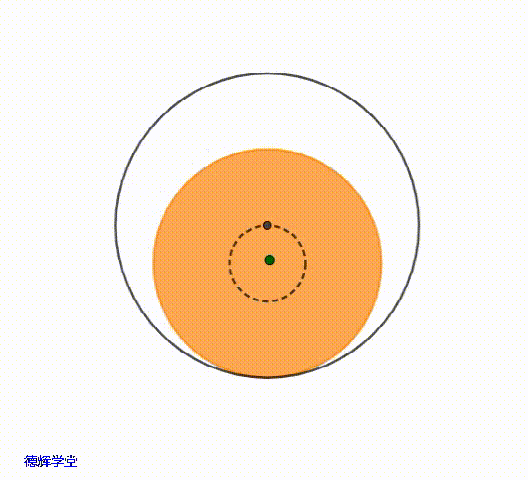
动画5 主定位孔中心的极限运动轨迹

2）副定位部分的孔销浮动

     副定位部分的主要功能是约束零件旋转的自由度，如果销孔之间有间隙存在，那么副定位孔相对于副定位销，就会有“旋转的浮动”，当然不是纯粹的旋转，还夹杂有平移，因为主定位孔在平移，必然会影响到副定位孔。

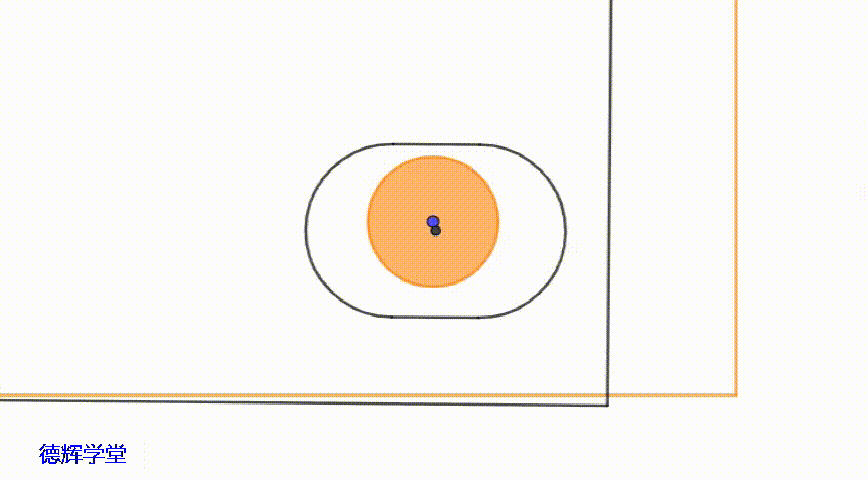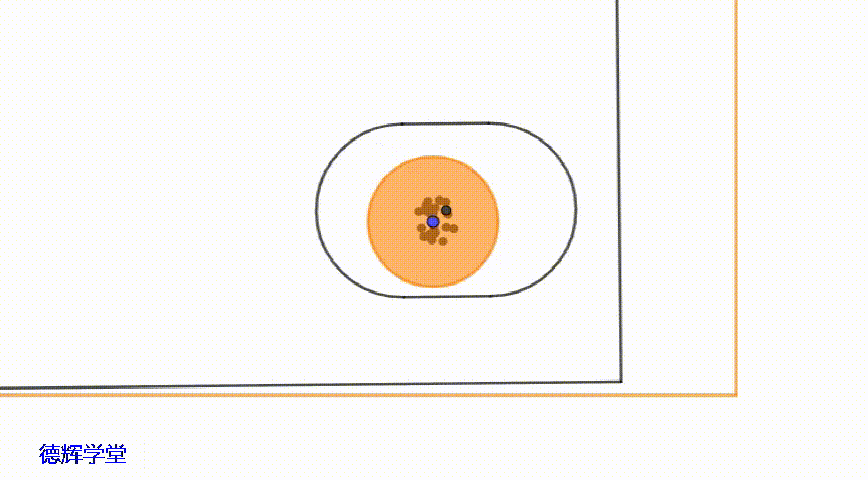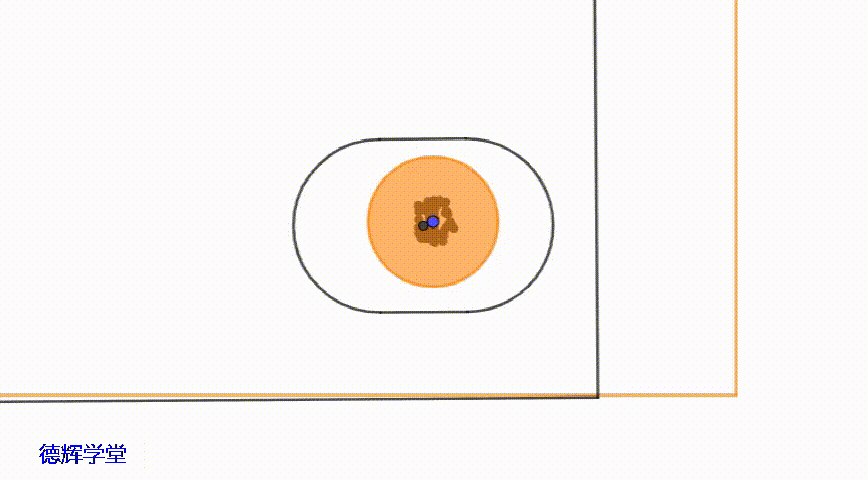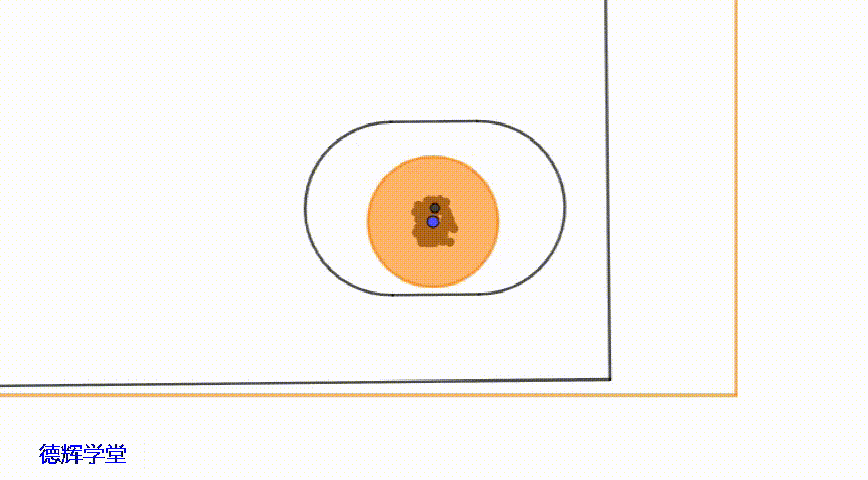
动画6 副定位孔中心的运动轨迹

如动画6中显示，副定位孔中心的运动轨迹的形状,相对复杂一些，其形状接近于一个“矩形”。具体见图6：

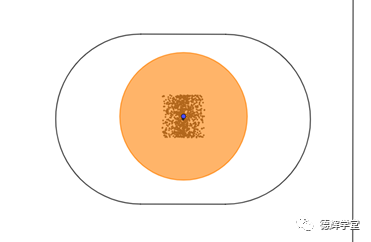
图6 副定位孔中心的运动轨迹

      下一章节，我们会具体研究它的数学轨迹。

3）安装孔的浮动

因为定位部分的浮动，导致整个零件都在“抖动”。所以，3个安装孔，也在被动的抖动，我们来观察一下它的运动轨迹。

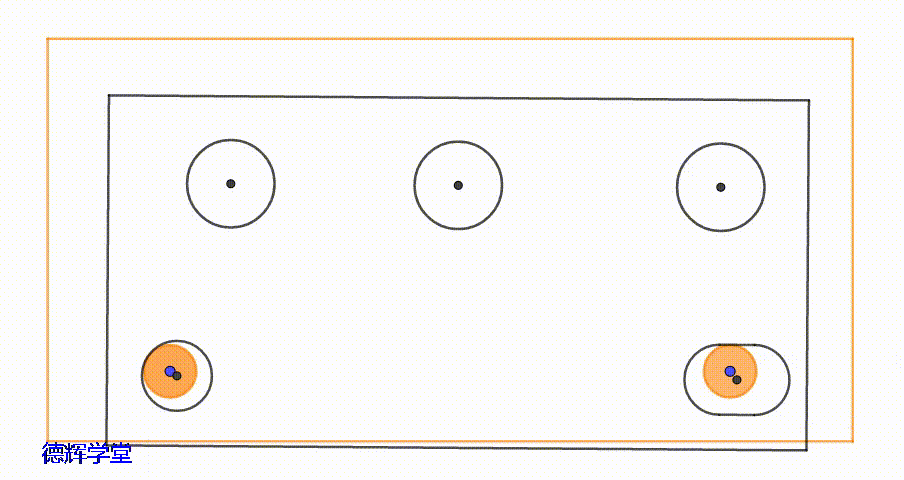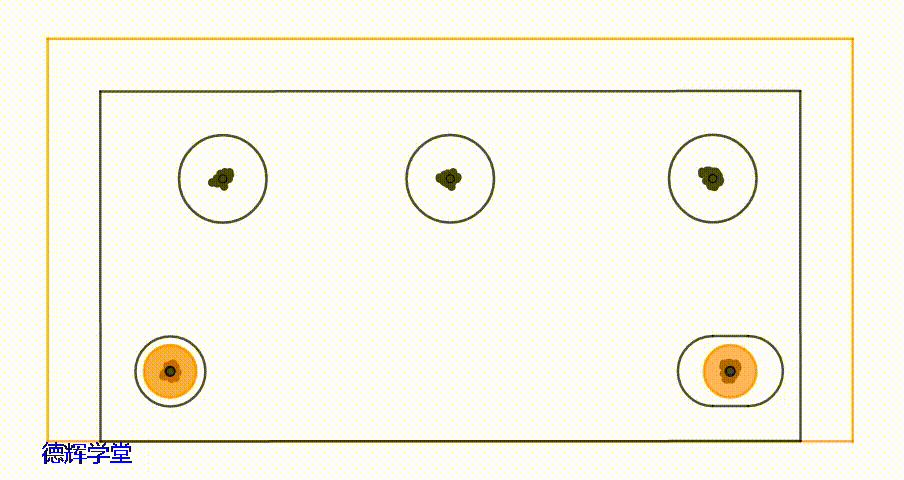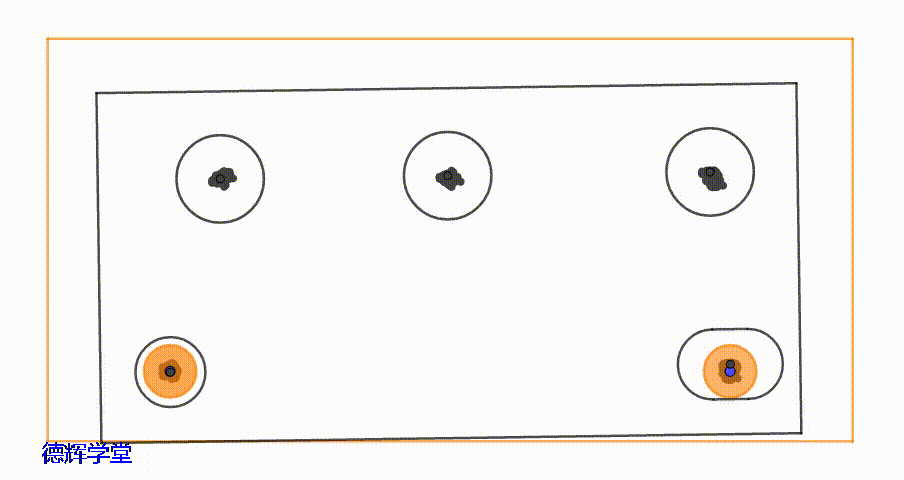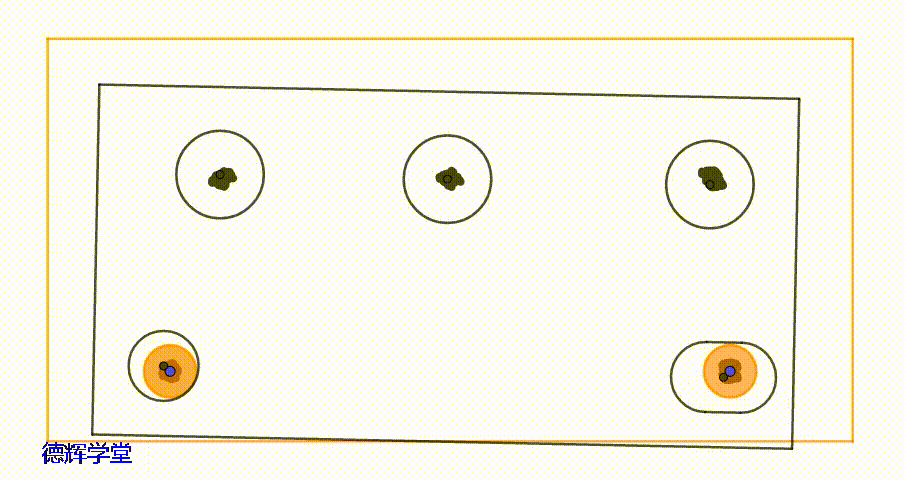
动画7 安装孔的运动轨迹

安装孔的运动轨迹会更复杂一些，总体看来有点类似一个“平行四边形”，而且处于不同位置的安装孔，它的运动区域形状都不一样。

大家先来感受一下安装过孔的活动区域，见图7，后边我们会详细解释区域的来源。

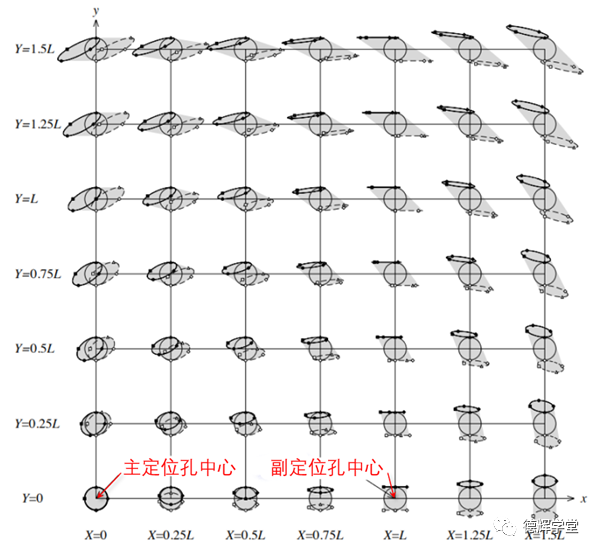
图7 处于不同位置安装孔的运动轨迹

2.    孔销浮动的数学模型

我们从上一个章节直观的感受了孔销浮动的现象。可是，如果要把它量化，就必须要把它的数学关系给它理清楚。

这个过程稍微有点痛苦，但肯定有价值。请大家跟着我的思路慢慢把它的数学关系给它理理清爽。

我们分析的整体思路是，先分析主定位孔的浮动，然后是副定位孔的浮动，最后是安装孔的浮动。

1）主定位孔的运动轨迹

我们现在已经知道主定位孔的运动轨迹，其实是一个圆形的区域。

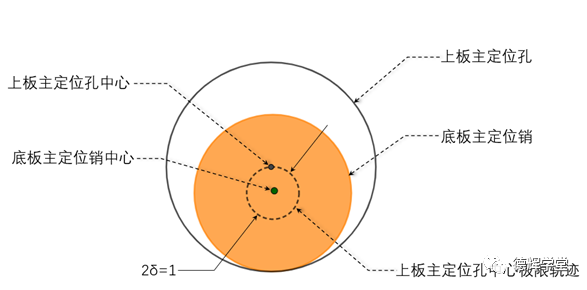
图8 主定位孔的运动轨迹

图8显示的是主定位结构中的销孔结构，以及主定位孔中心运动的极限轨迹，直径为2δ的圆。

图9 主定位孔中心B的浮动区域

图9显示的是主定位孔中心B的活动范围，要注意的是，主定位孔中心B的运动轨迹不仅仅是圆周，还包括在圆以内的区域。它是一个直径为2δ的圆形区域。

我们接下来就来研究，B点和底板主定位销中心O之间的关系。

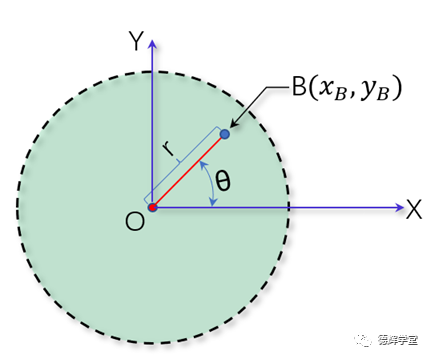
图10 B点坐标

见图10，我们先以主定位销的中心O点建立一个坐标系XOY, 再设定两个随机的参数，一个是BO的距离r, 另外一个BO连线和X轴的夹角θ（利用极坐标处理表方便）。

这两个独立的随机参数r和θ决定了B点在圆以内的随机位置。

显然，根据图10，我们知道r和θ的变化范围，r的变化范围在0-δ之间，而θ的范围是在0-2π之间。于是，我们就很容易得出B点在XOY坐标系中的坐标轨迹：

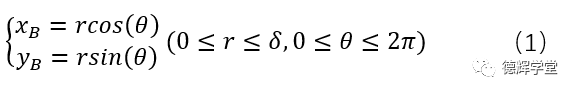
 公式（1）中，因为r和θ是两个独立的变量，同时也是随机的，所以会导致B点的坐标x_B和y_B也是随机的，而且，B点肯定会在图10中绿色的圆以内。

2）副定位孔的运动轨迹

根据图11中的装配图中所示，我们设副定位孔和主定位孔之间的距离是L（一个已知的值），而且副定位孔和副定位销之间的间隙也是同样δ（0.5），见图11。

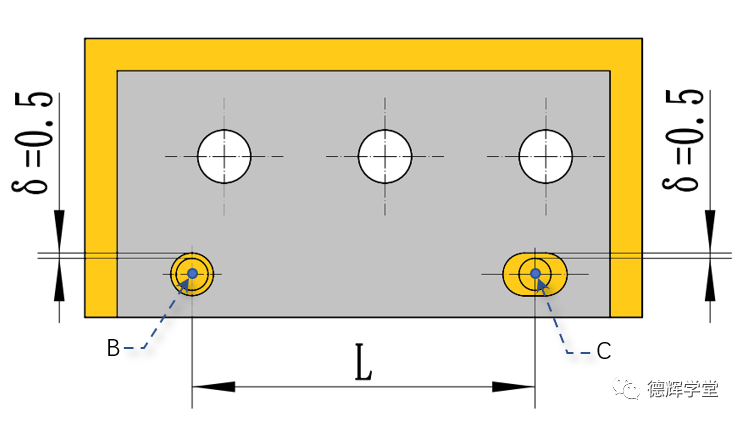
图11 装配图

如图11所示，我们先假设，副定位孔(长腰孔)的中心为C，它相对于黄色的底板，在上下方向（Y方向）上的浮动量为λ，不难得出结论，那么λ的变化范围是（-δ，+δ）。具体见图12，动画8和图13。

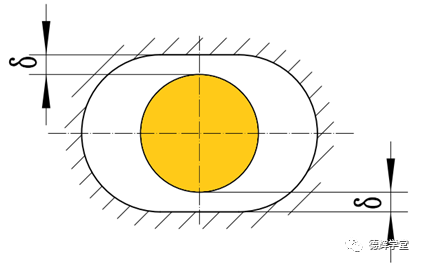
图12 单边间隙是δ

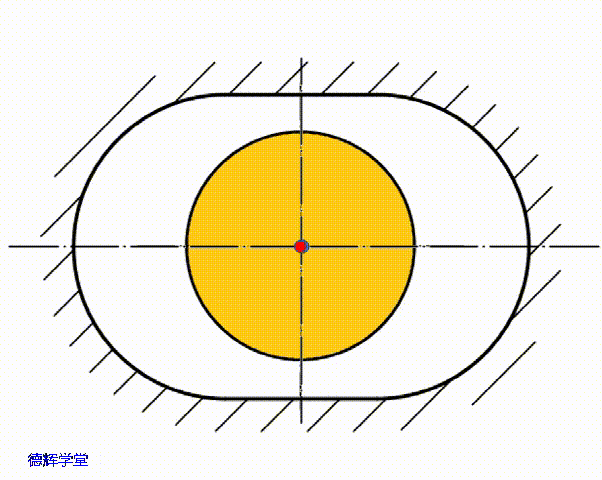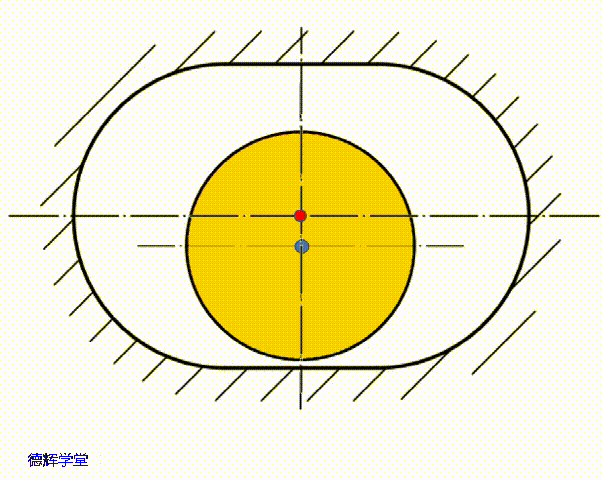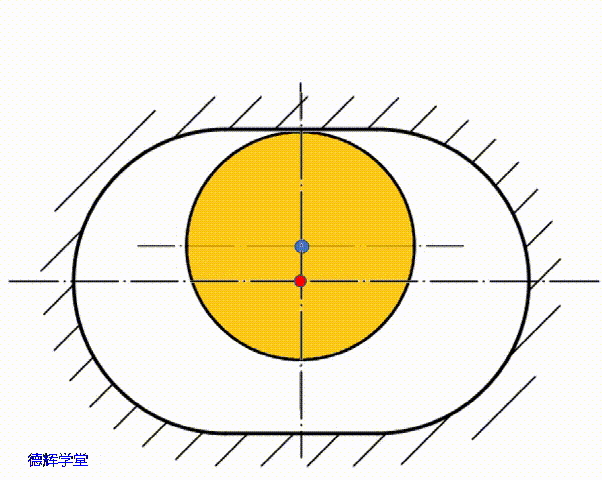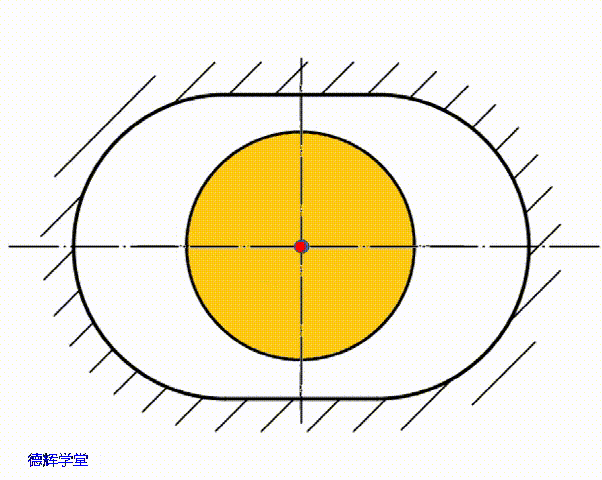
动画8 副定位孔上下浮动

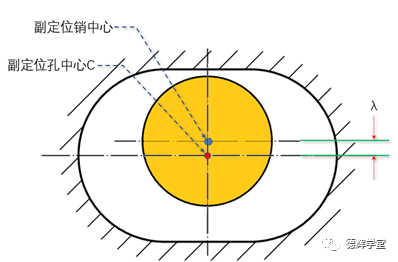
图13 副定位孔上下浮动量λ

根据图12，动画8，图13中的分析，我们不难得出C点的Y方向坐标为：

当然，λ也是一个独立的随机变量。

接下来，我们来求C点的X坐标x_c。

实际上，副定位孔的运动轨迹稍显复杂，它会受到主定位孔浮动的影响, 它的运动不仅牵涉平移，还有旋转，是一个“复合”的浮动，见动画9。

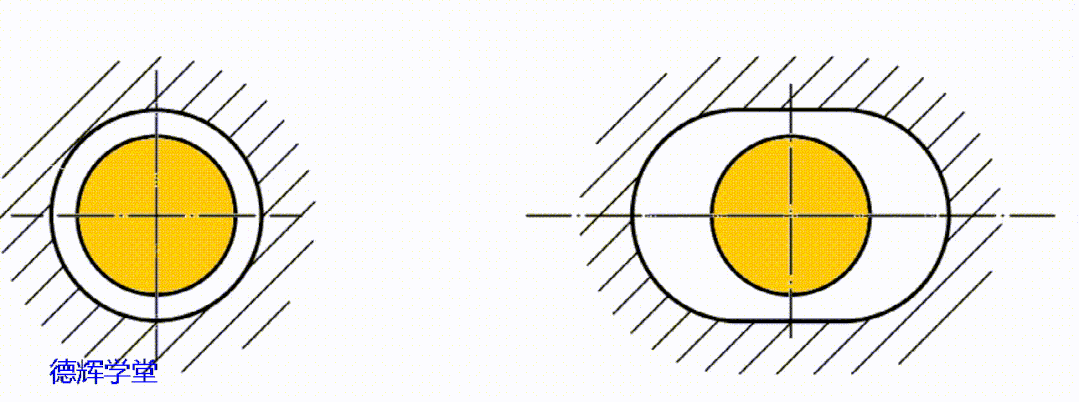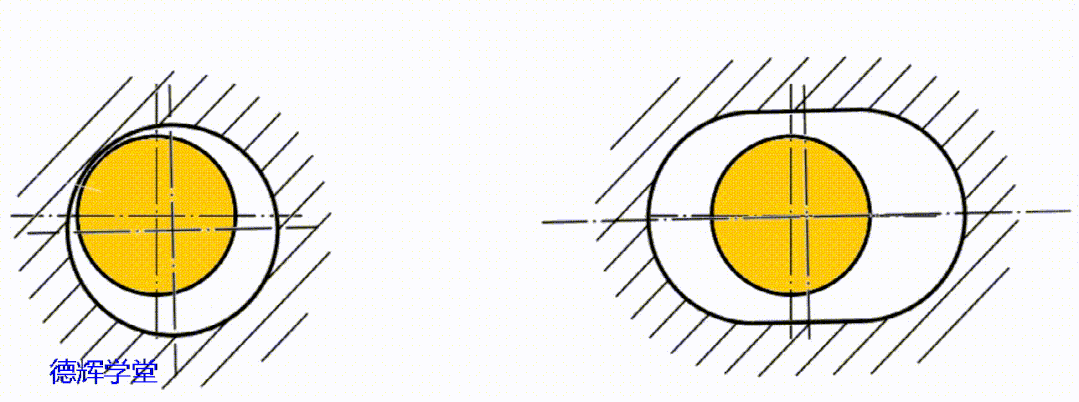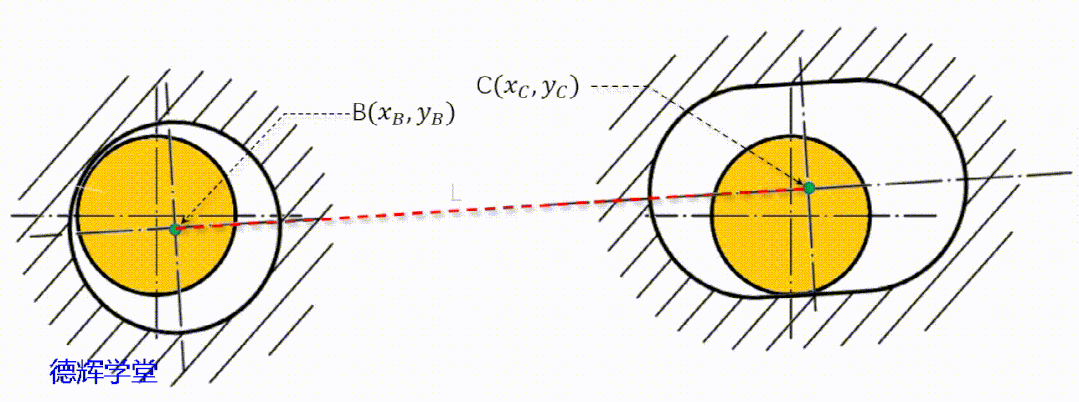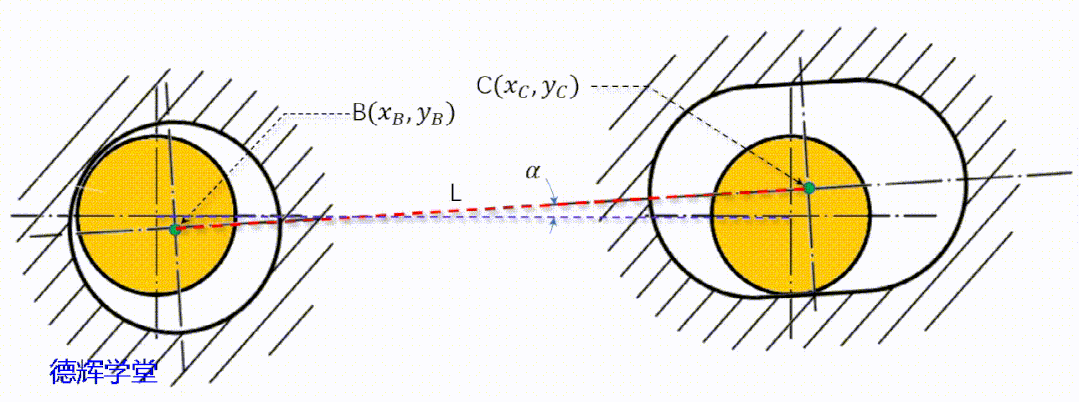
动画9 副定位孔的复合浮动

经过动画9中显示的两种合成的复合运动后，我们再来分析副定位孔中心C的轨迹。

见动画10，图14，我们先做一些辅助线，简化后，再来分析里边简单的数学关系。

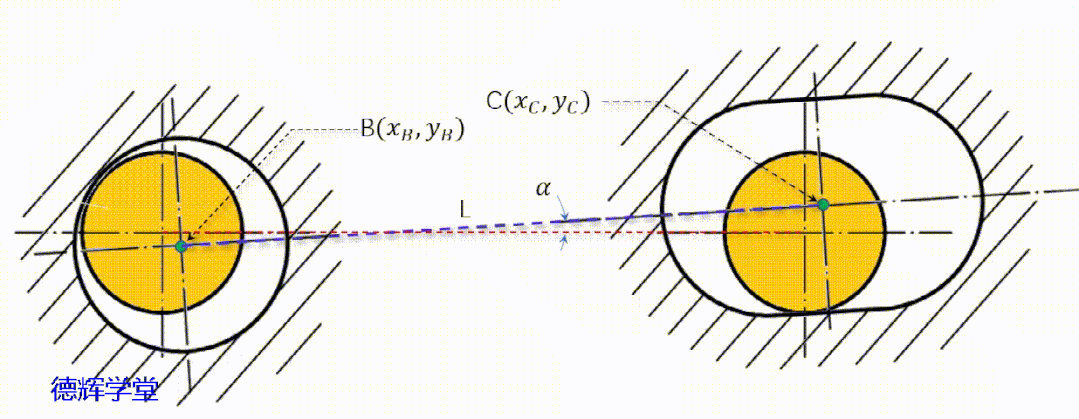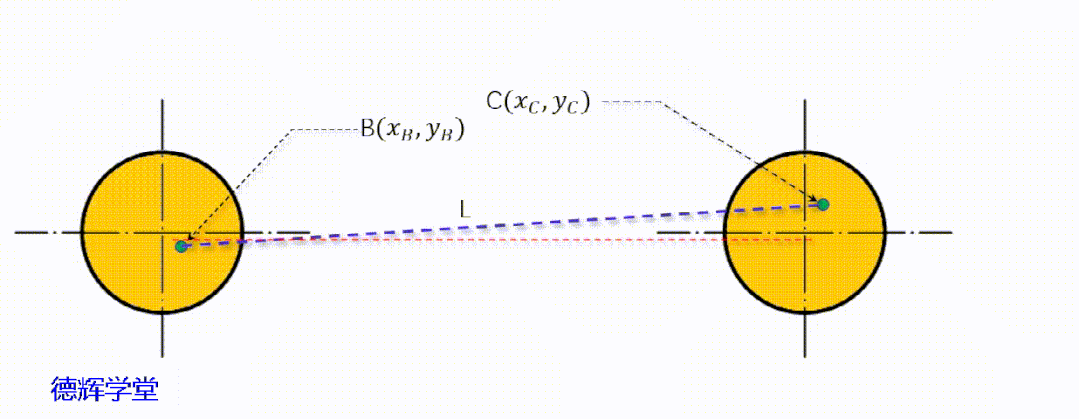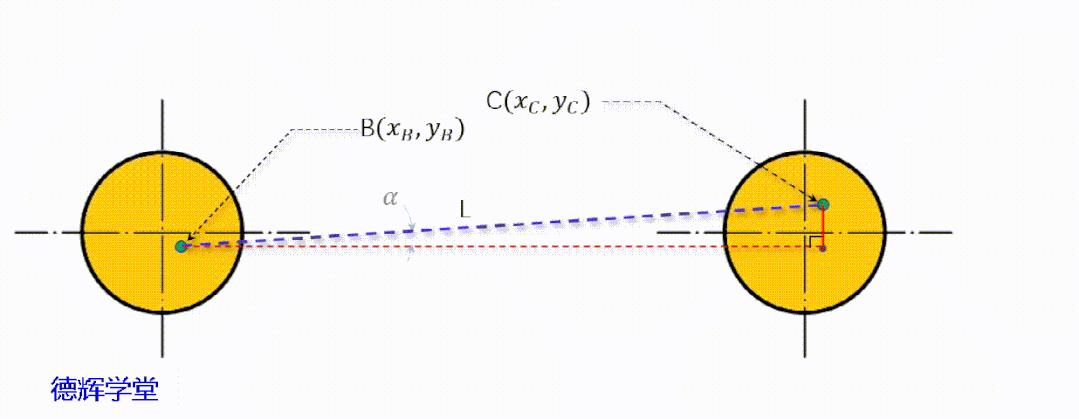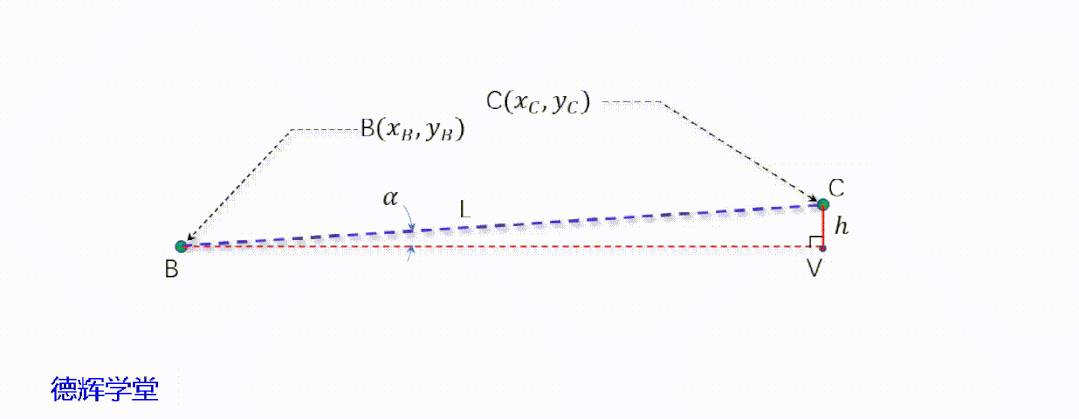
动画10 图形简化处理处理

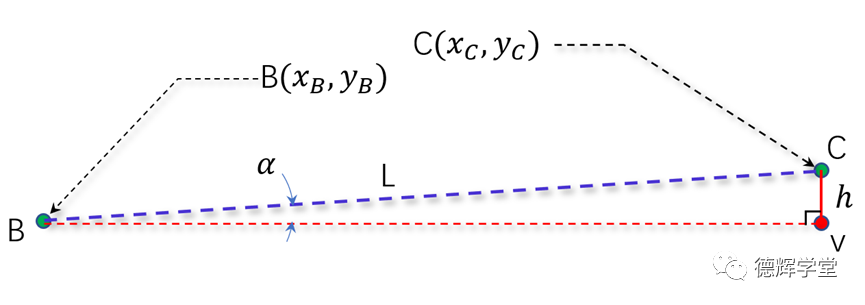
图14 副定位孔中心的坐标

见图14中的几何关系，显然BVC是一个直角三角形，我们不难得出h:

再结合公式（1）和公式（2），我写在下边：

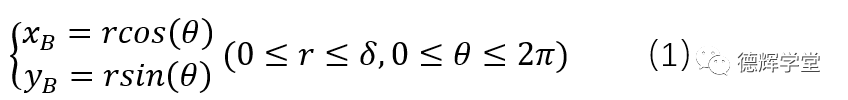
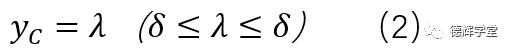
可以得出：

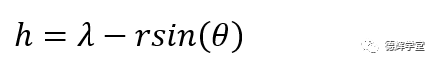
根据图14，h是直角三角形的直边, L是斜边，根据三角函数，我们就可以轻松算出图14中的旋转角度α：

请大家留意这个旋转夹角α，它很重要，我们后边还要反复用到。

有了旋转夹角α，我们就可以求出图14中的BV长度：

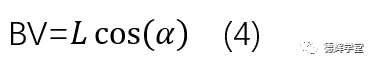
然后我们就可以轻易得出，图14中的C的X坐标：

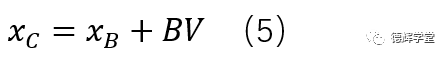
再结合公式（1）和公式（4），我们可以进一步将公式（5）整理成：

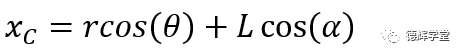
于是我们便整理得出副定位孔中心C，最终轨迹：

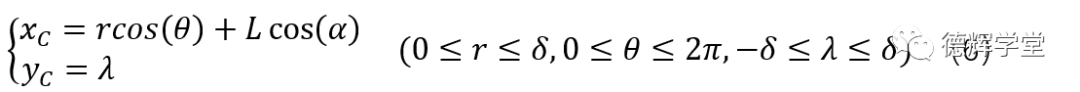
其中，公式（6）的α是由下面公式获得：

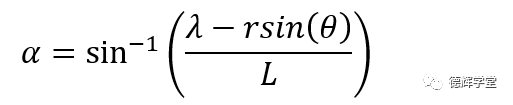
 公式（6）表达了副定位孔中心C的轨迹，推导的过程痛苦了一点，但是结果相对简单。实际上，C点的轨迹由3个独立的随机变量构成，一个是来自主定位孔的两个参数，r和θ，另外一个是来自副定位孔的浮动量λ。

3）安装过孔中心的轨迹

这个才是我们的重点。

我们知道了主定位孔中心B的轨迹，副定位孔中心C的轨迹，再来推导几个安装过孔的轨迹及相对容易了。

为了方便说明，我们先在上板建立子坐标系（这里只讨论平面坐标系）。我们把坐标原点建在B点，BC的连线作为x轴，这样零件的子坐标系xoy就建立了,见图15。

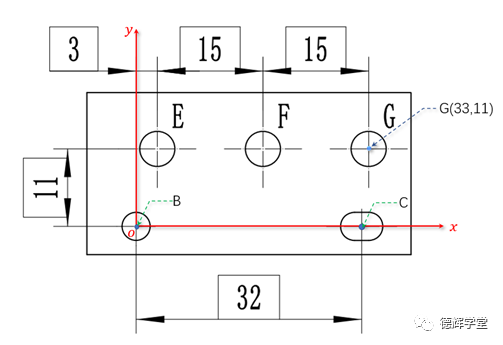
图15 上板和子坐标系xoy

图15中，我们把理论尺寸也标上去，因为这里不讨论零件自身的制造误差，所以我们就可以轻松得出3个安装过孔在子坐标系xoy中的具体坐标，比如说G孔中的坐标就是就是(33,11),写成代数形式：

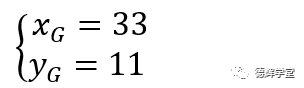
 注意，当零件加工好后，每个特征在子坐标系里边里的理论坐标是固定不变的。

而我们更加关心的是，在经历孔销浮动的震荡后，G孔相对于黄色底板的具体位置，或者说G孔在母坐标系里的具体坐标是多少呢？

在前面分析C点的轨迹时，动画9显示了两个零件的相对浮动状况，我们在动画9的基础上，将母坐标系XOY和子坐标系xoy给它建立起来。

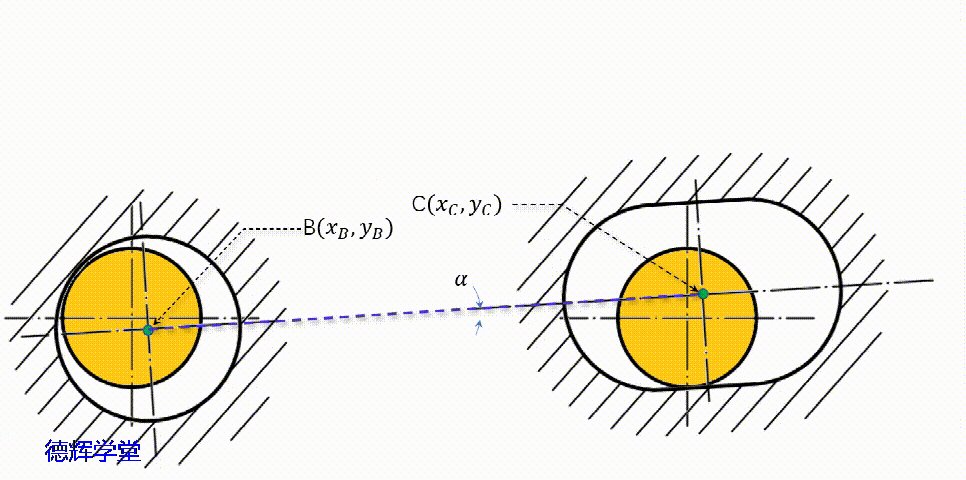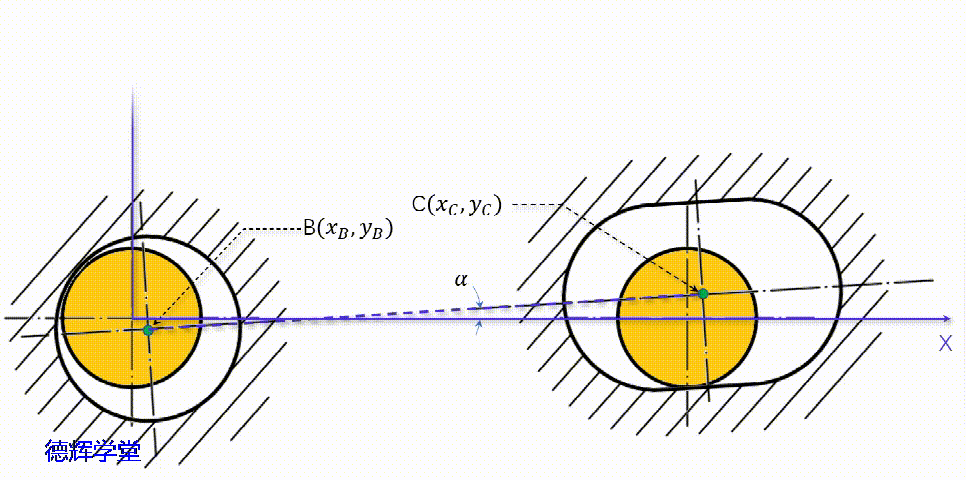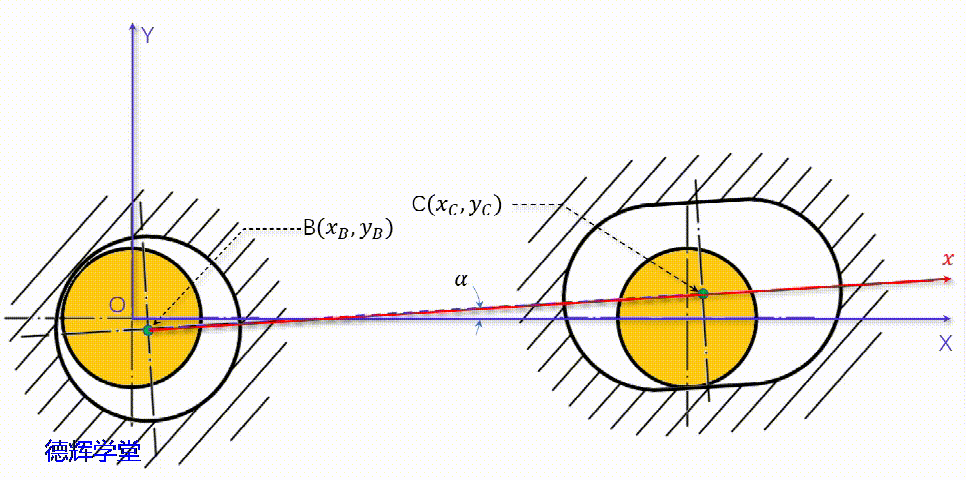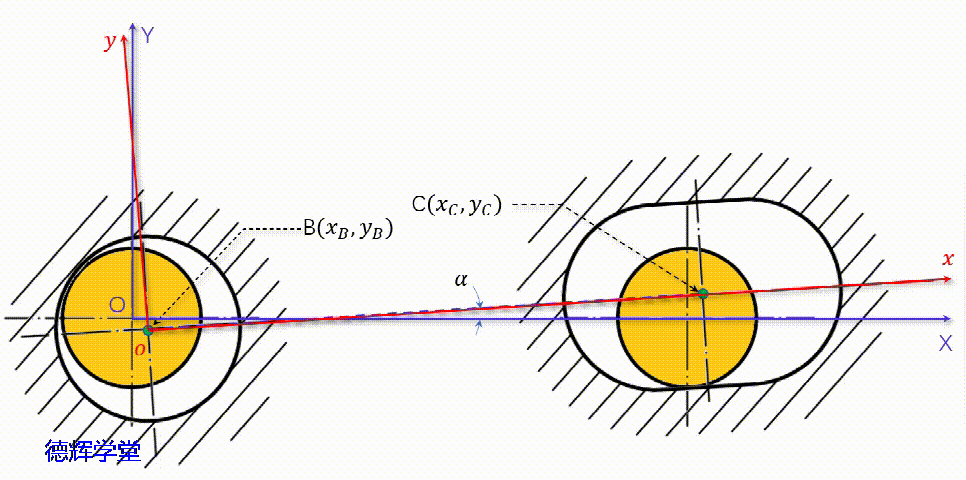
动画11 子母坐标系的建立

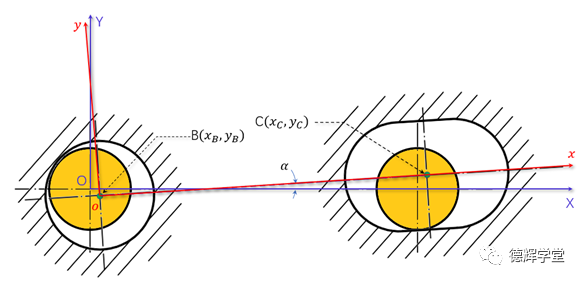
图16 子母坐标系

如果大家仔细观察图16中的两个坐标系，我们会发现两个特点：

     1）我们知道子坐标系的原点B，在母坐标系中的坐标（x_B,y_B）;

     2）我们还知道子坐标系相对于母坐标系旋转的相对夹角α;

知道这两个条件，我们就可以利用旋转加平移实现坐标变换了（如果对坐标变换不理解的小伙伴，建议看本文最后链接的文章《基准偏移7，坐标变换》）。

为了方便大家理解，我把坐标变换公式再一次写在这里，简要做一下说明：

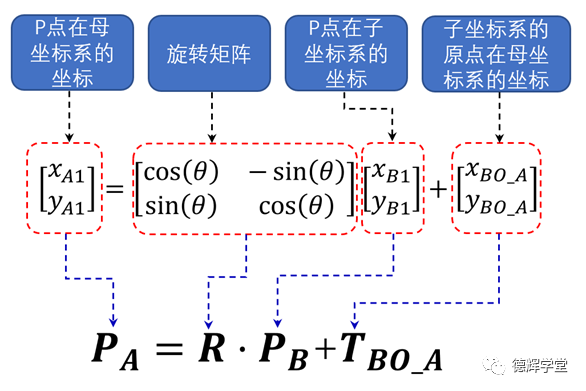
图17 坐标系变换公式

现在我们要计算图16中，G孔中心相对于底板（母坐标系）的具体位置，就可以直接套用图17中的公式。我们设G点在母坐标系中的坐标为（x_G’,y_G’）, 则有下面关系：

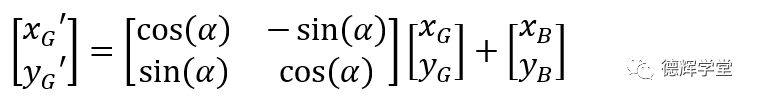
稍作整理得：

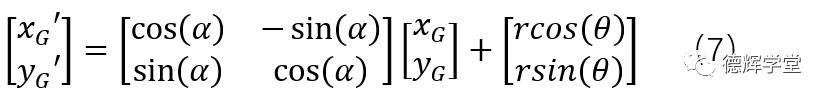
如果不嫌麻烦，我们再将公式（7）展开成方程组的形式，最终便得到了安装孔中心G的坐标轨迹:

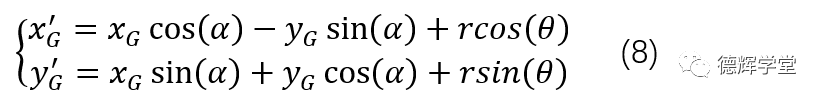
公式（8）中的一些参数，受到下面条件的限制：

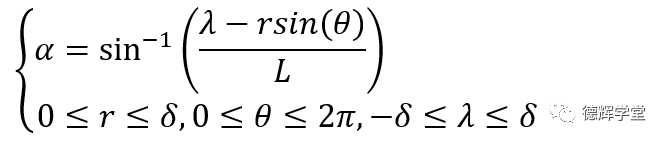
公式（8）是我们推导到现在得到的结论。

公式（8）看起来牛逼，苦逼的样子，但是，仔细观察，会发现x_G和y_G是已知的，在本案例中就是（33,11），其余的说穿了就3个独立的变量，r, θ，λ，而且3个变量的范围我们已经很清楚，所以，根据公式（8），我们就能够确定上板G孔中心，相对于下板可能的运动轨迹了。

根据蒙特卡洛的思路（如果您对所谓的蒙特卡洛法也感到懵逼，看本期文章后边的链接文章），我们用软件（甚至Excel），随机产生3种参数r, θ，λ（在各自允许的范围内），产生参数的个数看心情，尽量多吧（建议大于500个），然后再带入公式8，就可以计算出G点在母坐标系中的坐标（x_G’, y_G’）。

因为输入了500套随机参数r，θ，λ，我们就可以得到500个G点的随机坐标（x_G’,y_G’）。这样我们就可以观察，在孔销浮动过程中，安装过孔中心G的轨迹。

软件的操作过程，这里不再赘述，大家直接看结果吧：

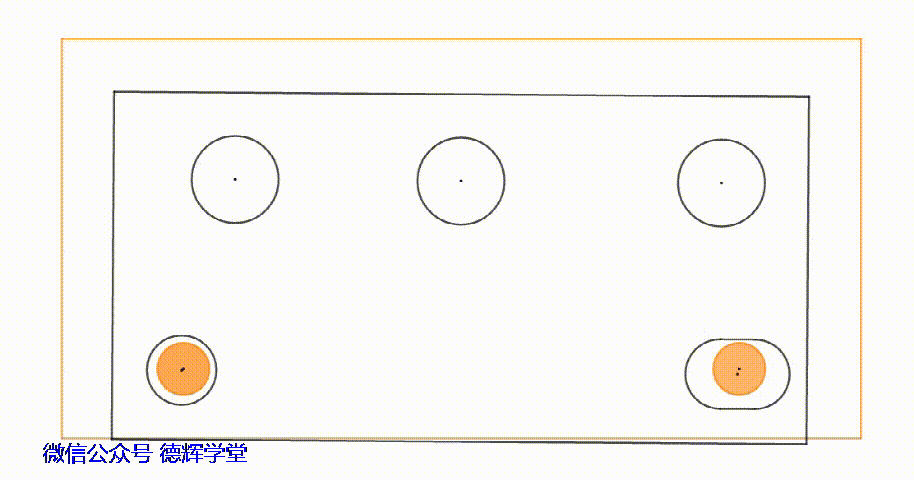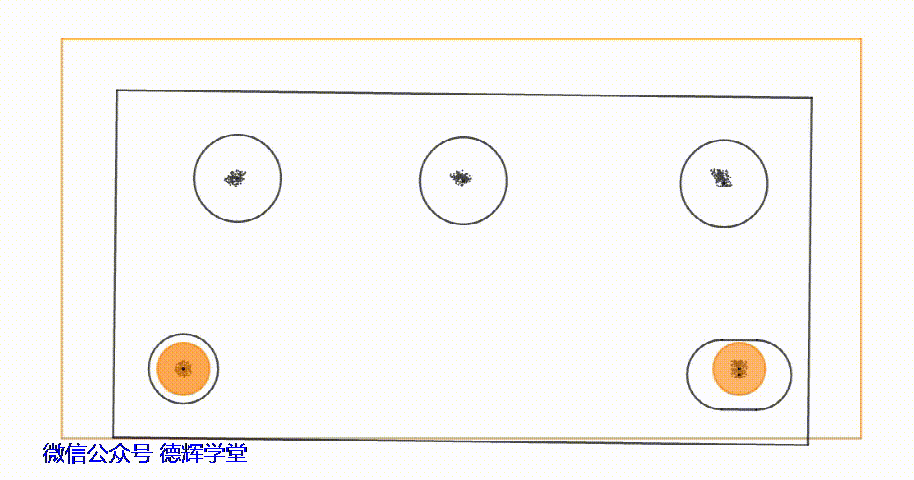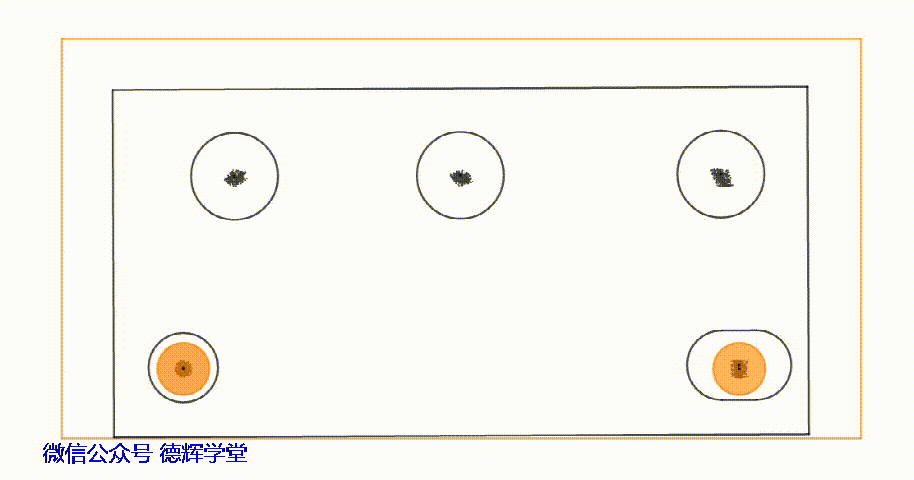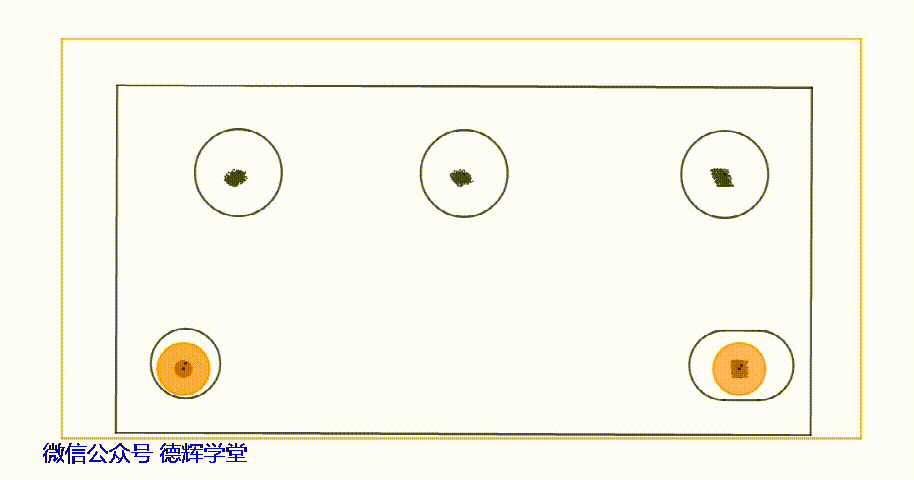
动画12 安装过孔中心G的轨迹

大家如果仔细观察动画12中，安装过孔中心的轨迹，就会发现，在孔销浮动时，安装过孔中心所经历的区域类似一个“平行四边形”的区域。

而且，安装过孔的位置不同，经历的区域形状也是不一样。

日本学者Shinya SUZUKI 和Noboru WAKAYAMA把针对不同坐标位置的过孔中心，所经历的区域都描述出来，我就将他们的图直接放在下边，供您观赏：

图18 安装过孔中心轨迹

仔细观察图18中的图形，我们会发现距离主副定位孔越远的地方，过孔中心浮动的范围就越大。见图19中最右上角红圈处的那个夸张的图形。

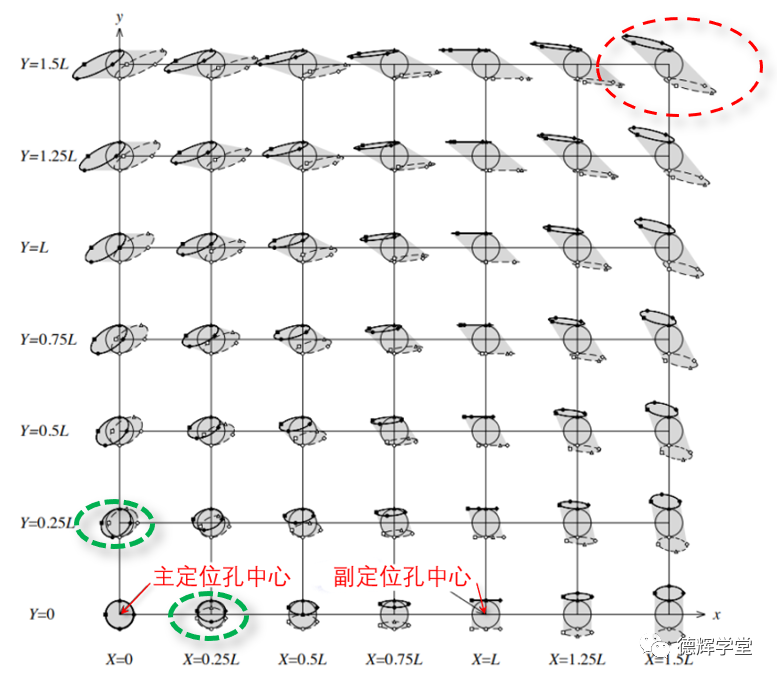
图19 不同位置特征的浮动轨迹

而距离主副定位孔（尤其是主定位孔）越近的地方，过孔中心浮动的范围相对偏小（但是最小的也比主定位孔中心浮动的圆形区域要大）。见图19中绿圈部分的区域。

很多定位结构中，有经验的设计工程师在设计定位销，或者定位孔的时候，会故意把定位特征之间的距离拉得很开。

您，现在理解其中的原因了吗？

到这里，我们还不能停下，我们还需要对安装过孔的轨迹进行放大研究。

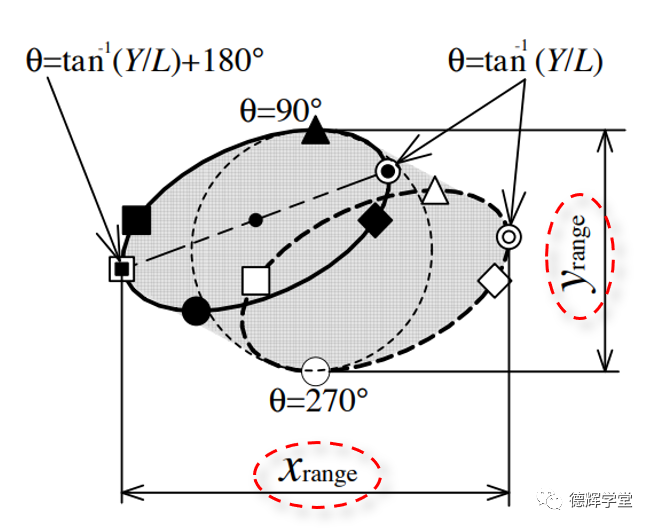
 图20 安装过孔中心的轨迹

图20显示的是，在孔销浮动的过程中，安装过孔中心点的浮动范围（图中灰色区域，截取的是文献原图），它是一个类平行四边形区域。

保守的工程师们更加关心的是，安装过孔中心的浮动范围，x方向浮动的最大范围x_range是多少？y方向浮动的最大范围y_range是多少？

对于机加工，或焊接来说，这就是定位误差；对于基准偏移来说，这个就是补偿量（以后在详细讨论这个话题）。

图20中的x_rang和y_rang，我们利用公式（8）是可以推导出来的。因为整个推导过程比较复杂，还需要利用偏导和近似处理之类的数学知识，整个过程我就不再这里啰嗦了，我们还是直接享用专家们的学术成果吧：

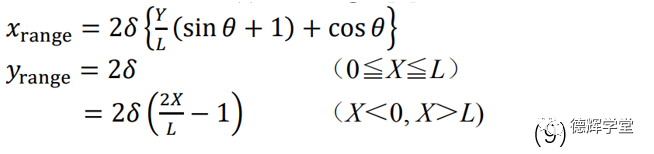
上式中：

     1）X,Y表示安装过孔在子坐标系（基于圆孔和长腰孔建立的坐标系）中的理论坐标；

     2）δ表示定位孔和定位销之间的单边间隙（主副定位特征间隙都是δ）；

     3）L表示长腰孔中心（副定位孔）到圆孔中心（主定位孔）的距离；

     4）θ的值由公式θ=arctan(Y/L)得到，它也是产生极值的条件。

根据图20中图形的对称特性，我们把安装过孔中心处理成X方向和Y方向的线性尺寸：

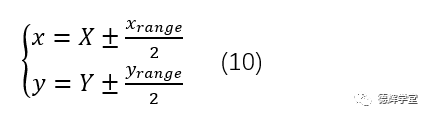
公式（10）中，

     1) x，y表示安装孔的中心，因为孔销浮动，在母坐标系中，在X方向和Y方向的实际坐标范围；

     2) X，Y表示安装孔中心在子坐标系中的理论坐标；

     3) x_range，y_range则如公式（9）中表达的，安装孔中心因为孔销浮动的变化范围。

这样，如果我们要计算一维的尺寸链，就可以套用公式（10）了。

好了，本期的文章先到这里，希望本期文章对您有所帮助。

下一期文章，我们再来探讨基于本期文章所提供理论基础的实际应用。

本期小结

本期文章的主要内容，是研究一面两销配一面两孔（其中一孔是长腰孔）的定位结构中的孔销浮动，以及孔销浮动带来的影响。

第1章节描述了定位特征之间的间隙存在，会导致孔销浮动的产生，孔销浮动会在主定位特征之间，副定位特征之间都有产生，从而导致整个零件相对另外一个零件都在不断的“浮动”。

第2章节我们从数学的角度出发，探讨了主定位孔浮动的数学轨迹，副定位孔浮动的数学轨迹，还有其他特征被动浮动的数学轨迹，为我们后期做公差分析奠定了理论基础。

 【后记】

在我过去的设计和顾问咨询经历中，经常会遇到孔销浮动的问题，搞清楚孔销浮动，尤其是多个孔销浮动的数学关系一直是我的想法。虽然VSA，3DCS等公差分析软件会给我们一个准确的结果，但是却没法搞明白其中的缘由。

直到有一天我看到日本长野大学（Nagano College）的学者Shinya SUZUKI 和他的合作者在2019年发表的关于孔销配合的论文，论文中详细描述了孔销浮动的数学关系。而且这位仁兄，不仅仅研究了圆销对长腰孔的数学关系，还那研究了圆销对圆孔，菱形销对圆孔的数学关系，对我启发很大。

所以，需要申明的是，本期文章的理论原型并非我个人原创，我只是传播者。

当然，还需要说明的是，上面的理论并非完美，还有很多问题亟待解决：

    1. 既然其它特征的被动运动轨迹是一个类平行四边形区域，一般极值点会发生在4个角上，但是如果我想知道特定方向的变化范围，如何求得？比如图21中，我想知道N方向的极值点A，如何求呢？因为我们在分析轮廓的时候（比如缝隙，面差，均匀度），实际轮廓的法向很有可能并非X向，也非Y向, 而是某个特殊的方向。

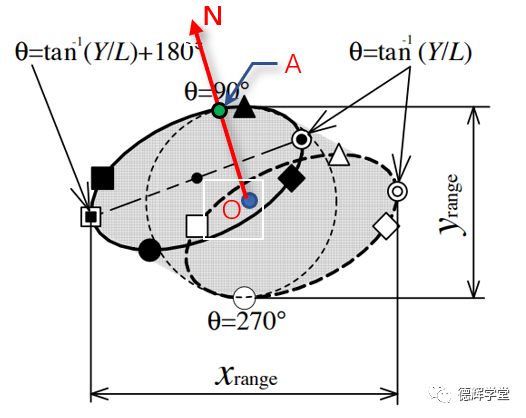
图21 特定方向的极值

    2. 上述理论求得的x,y的变化范围是基于极值理论，而对于现实生产设计指导意义最大的还是基于概率统计，如何结合概率统计来分析呢？这也是一个需要解决的问题。

    最后，要感谢我的学生，江苏理工学院在读研究生汤丽媛的协助，她帮我筛选和下载了不少论文，为我提供了有效的学术参考。

    如果您对本文有任何不同的看法，或者建议，欢迎在留言区给我们留言！

参考文献：