数统治着宇宙

               --毕达哥拉斯

**********************************************

本期我们来探讨一下尺寸链计算。

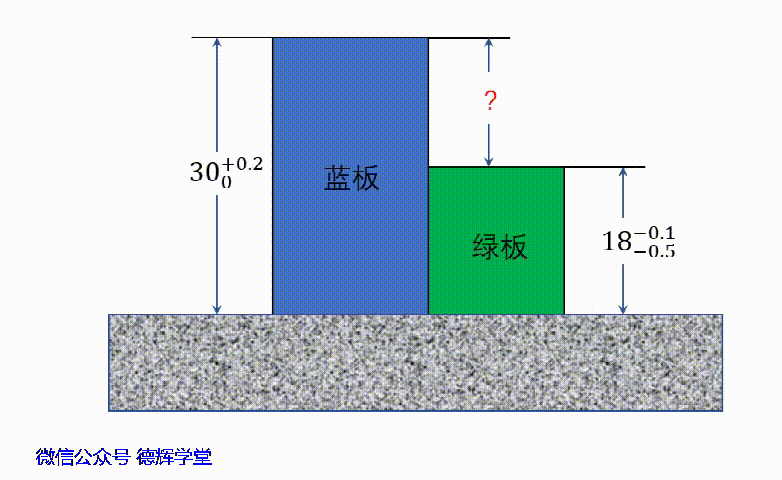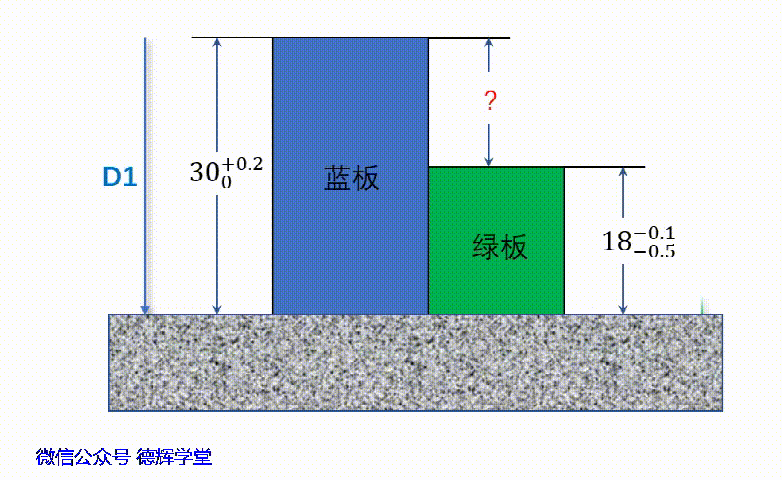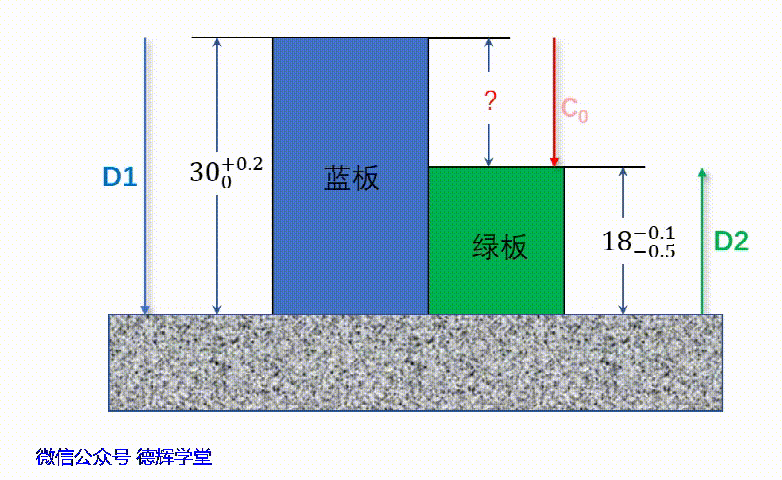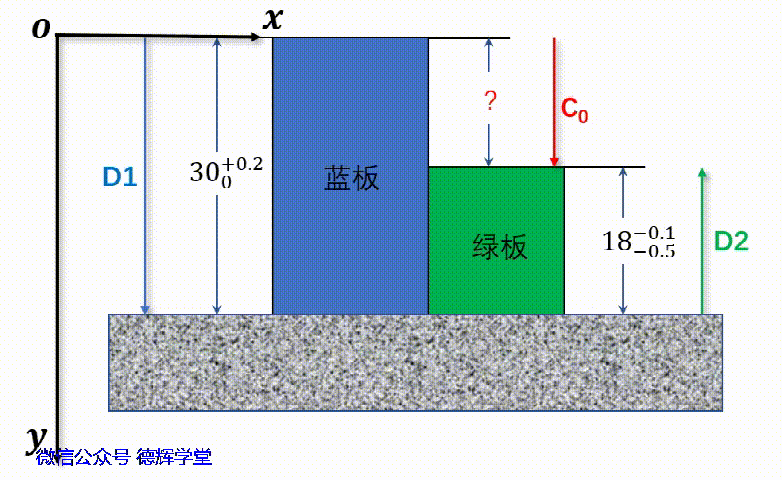
先来看一个题目，见图1，有两块板，分别为篮板和绿板，放在大理石平台上，每块板的高度已知，求两块板的高度差C₀（不考虑形位公差）。

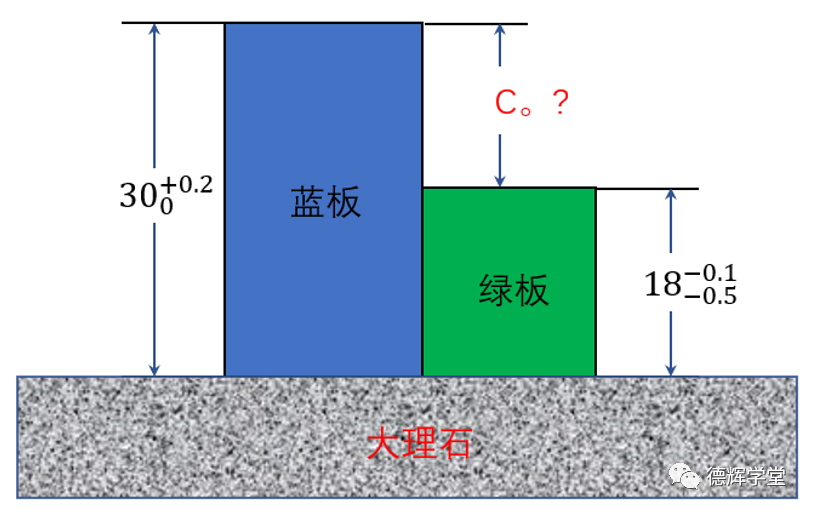
图1 求高度差C。

对设计工程师来说，这其实是一道再简单不过的计算题目。我在上课的时候，通常会告诉工程师们，用简单的三步法就可以搞定：

第一步，将所有相关的尺寸公差转化为对称公差。比如，蓝板的高度转化后为30.1±0.1，而绿板的高度为17.7±0.2。

第二步，封闭环的尺寸部分等于增环的尺寸之和减去减环尺寸之和。在图1中，很显然，C₀是封闭环，蓝板的高度30.1±0.1为增环（它变化趋势和C₀一致），而绿板的高度17.7±0.2为减环（它的变化趋势和C₀相反），所以C₀的尺寸部分为：

D_C₀=30.1-17.7=12.4

第三步，封闭环的公差部分是增环公差之和加上减环的公差之和。蓝板的公差为±0.1， 绿板的公差为±0.2, 所以封闭环的公差为：

T_C₀=±（0.1+0.2）=±0.3

所以我们可以得出最终封闭环C₀（也就是高度差）的变化范围是：

C₀=12.4±0.3

计算表格如下：

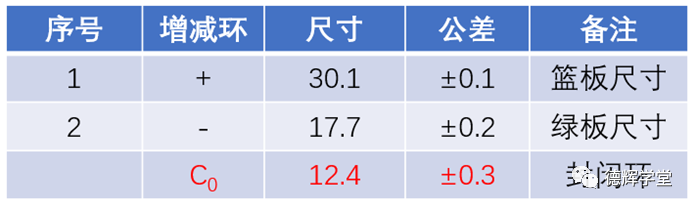
图2 计算表格

好了，尺寸链计算到这里就欧了。

事实上，很多聪明的工程师，哪怕不知道所谓的三步法，仅凭借直觉，也能将这个封闭环的结果给计算出来。

记得有一次，我在给学员上尺寸链的课，讲到这里的时候，一位年长的工程师严肃的问我，吴老师，你讲的三步法是属于经验技巧还是有理论依据？

这是位严谨的工程师，他的言下之意非常明确，如果我讲的所谓三步法没有理论依据，仅仅属于经验技巧的话，那么它的通用性可能会受到质疑。如果有理论依据，那么理论依据是什么呢，可靠吗？

本期文章的主题，我们就是来讨论一般线性尺寸链计算后边的理论依据。

本期的文章分为2部分：

     1. 矢量累加和尺寸累加

     2. 区间分析和公差累加

本期文章比较长，但是难度不大，如果您对尺寸链计算后边的数学原理感兴趣，欢迎您耐心看完。

1.    矢量累加和尺寸累加

本章节我们分为两个小节来讨论，首先快速普及一下矢量相加的基本知识，然后再来讨论尺寸累加。

     1）矢量和矢量累加

在本公众号前面的文章中，我们就介绍过矢量，它是一个比较特殊的存在，它不仅仅有大小，还有方向，比如力。

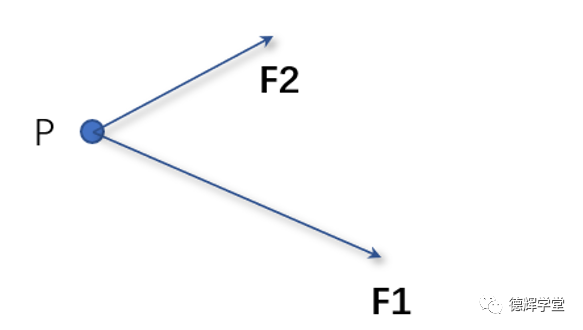
图3 一个物体受到两个力

见图3，我们高中就学过，如果一个物体P受到两个力F1和F2的作用，如何求这个物体P所受到的合力呢？

注意，这里F1和F2是被加粗的，本文表达的是矢量。

以前老师教过我们用平行四边形法或者三角形法求合力，见下面动画：

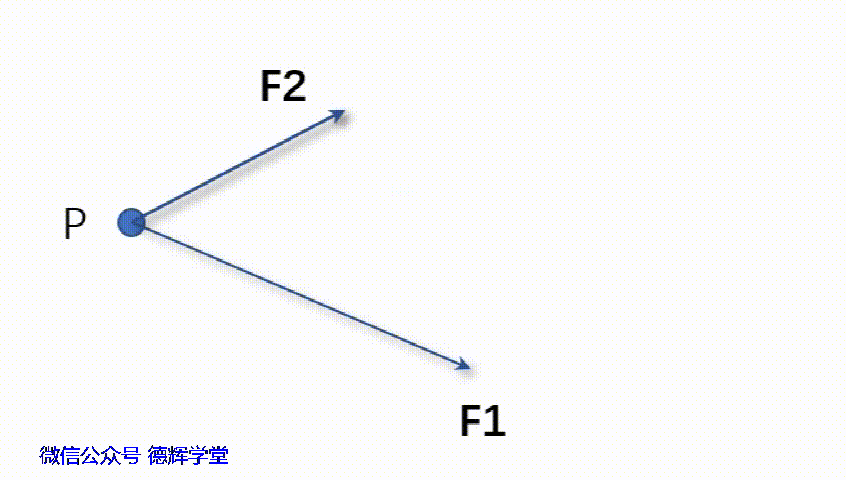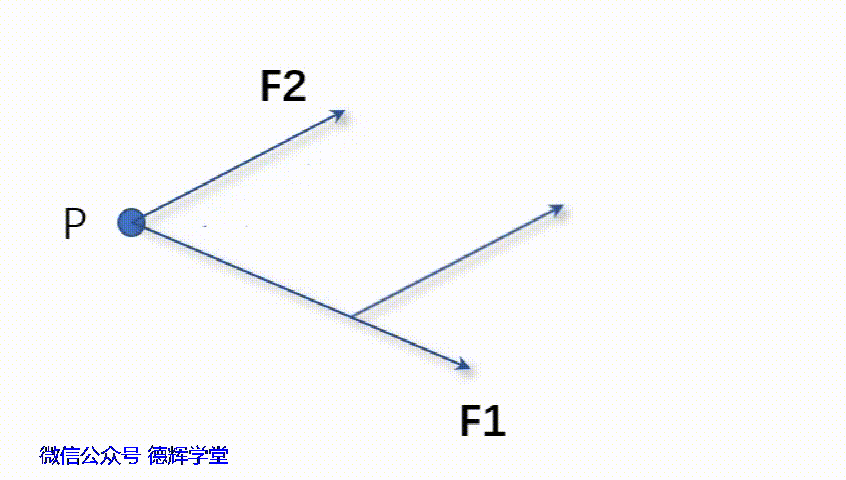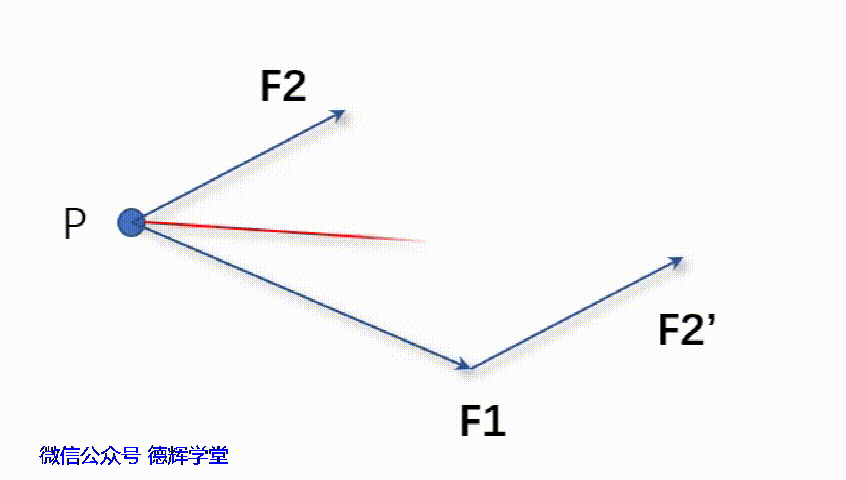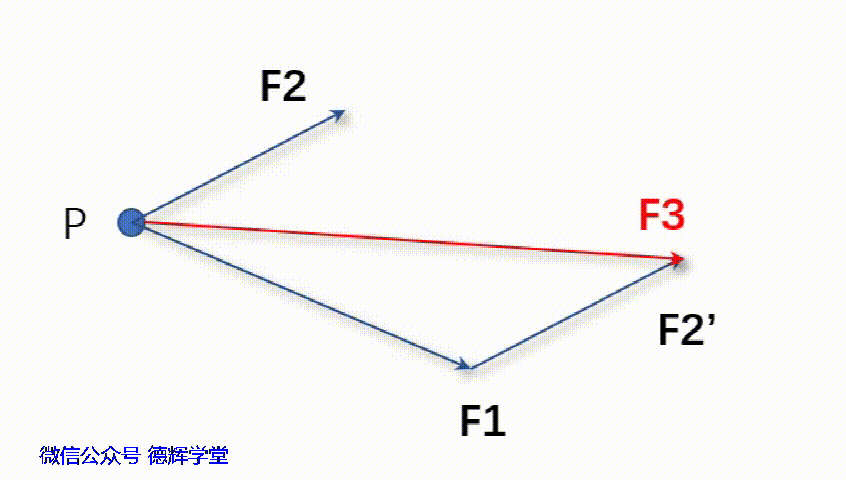
动画1 三角形法求合力F3

根据动画1可知，将F2平移后得到F2’显然有:

F3 = F1 + F2’    (1)

又因为矢量平移不改变矢量的性质，所以F2 = F2’, 那么由公式（1）可以得出：

F3 = F1 + F2    (2)

需要注意的是，等式（2）尽管成立，但是并不代表F3的大小等于F1的大小再加上F2的大小（我假设你知道三角形三条边的那个不等式）。

到这里，可能有小伙伴要问下面两个问题：

     1. 为啥矢量可以任意平移？

     2. 如果力的大小不能直接相加的话，那公式（2）对计算合力来说有啥意义？

关于第一个问题，做一个简单说明，我们上学那会儿学的矢量都是“自由矢量”，人们只关心矢量的方向和大小（也就是长度），不关心位置，所以当我们任意平移矢量的时候，矢量的方向和大小并不会改变，所以可以任意平移。

（注意，我们讨论的自由矢量，可以任意平移，但是有些矢量，比如位置矢量，线矢量，旋量等，和位置相关的，不能随便移动的）。

关于第二个问题，如果矢量的表达是使用坐标或者代数式来表达，公式（2）就有非常重要的意义。（事实上，矢量有很多计算规则，比如加法，减法，点乘和叉乘等，本期只讨论加法）

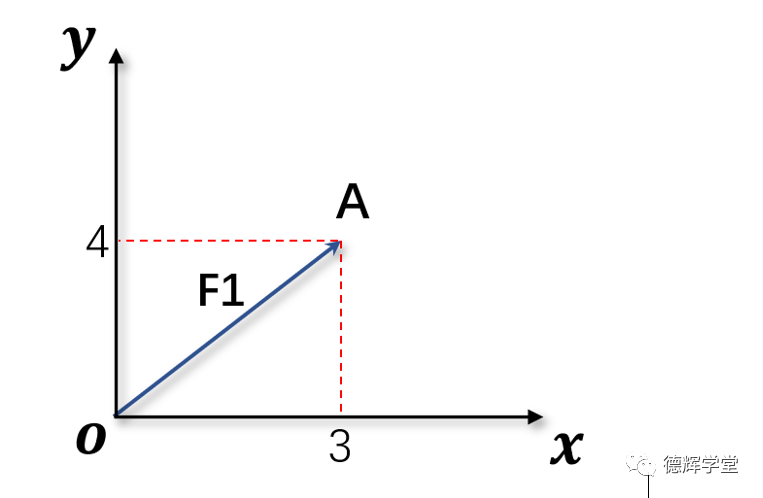
图4 矢量在坐标系中

如图4所示，有向线段OA表达的就是矢量（或者叫向量），A点的坐标是（3,4），如果用坐标表示矢量，则有下面关系：

F1 = OA = (3,4)

也可以用代数式来表达矢量，如下所示：

F1 = OA = 3i+4j

其中 i, j 分别表示x轴和y轴的单位矢量（这些概念公众号的往期文章都有介绍哦）。

矢量的坐标表达可以帮助我们理解它的几何意义，而矢量的代数式表达，可以帮助我们计算和推演。本期文章，我们两者都会用到。

需要特别注意的是，当用坐标表达矢量的时候，矢量的起点（没有箭头的那一端）必须放置在坐标系的原点，此时，箭头尖的坐标就是矢量的坐标。请再仔细观察图4中的OA.

如果矢量的起点不在原点，怎么求矢量的坐标呢？见图5A，如何求矢量O’A的坐标？

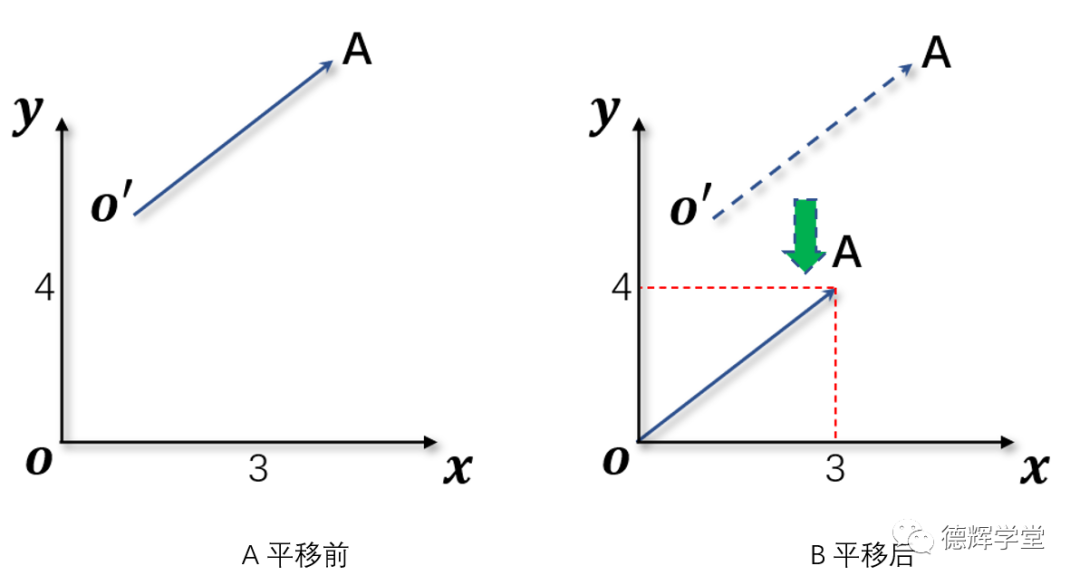
图5 平移矢量求坐标

图5中的A图，这时，我们是不知道矢量O’A的坐标的，但是，如果我们将O’A向下平移（再说一遍，平移不影响自由矢量的性质），使得O’点和坐标系原点重O合，见图5中的B图，这时，A点的坐标就是矢量的坐标。即有：

O’A = OA = (3,4) = 3i+4j

明白了么？当然，这些特点和性质是哪些牛逼的数学家们发现或者约定的，这样做有很多好处，比如，我们如何求O’A的长度（或者力的大小，或者叫矢量的模）？根据图5中B中的几何关系，不难求出：

|O’A| = |OA| 

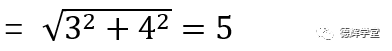
 矢量的模很重要，因为我们算尺寸链的时候，无论是缝隙，面差，过盈量之类的，我们关心的是大小(矢量的模)，而矢量本身我们不太关心。

矢量一旦用坐标来表达，矢量相加的计算就是小儿科了。我们直接用代数式可以来体验矢量相加的好处：

如果F1=ai+bj,  F2=ci+dj，那么有：

F1+F2 = (a+c)i+(b+d)j

看到没？直接将X坐标相加，Y坐标相加（如果有Z坐标的话，如法炮制），分别作为新的X和Y, 这样就得到了矢量相加的结果。

举个例吧。

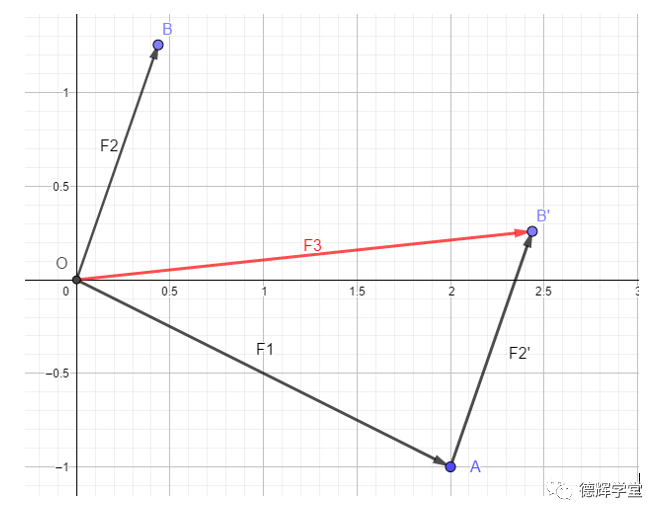
图6 矢量和的计算

见图6，已知矢量F1 =OA = (2,-1)； F2 = OB = (0.44,1.26)；已知F3 = F1+F2，求矢量F3的坐标和长度？

如图6中所示，根据三角形法，将OB平移，使得O点和A点重合，那么就有:

F3 = F1 + F2 = OB’

图6中的红色矢量就是两个矢量相加后形成的新矢量F3，这是F3的几何解释。

那么它的坐标是多少呢，我们可以用代数式直接计算：

F3 = F1 + F2 = （2i-j）+（0.44i+1.26j）

            =(2+0.44)i+(-1+1.26)j

            =2.44i+0.26j

所以矢量和F3的坐标为（2.44, 0.26）。再根据勾股定理F3的长度为：

|F3|

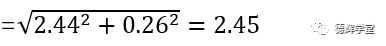
 搞定。

如果仔细观察图6中矢量之和，以及箭头的规律，我们就会发现，如果一串矢量首尾相连，比如F1和F2’（甭管有多少个矢量），然后我们做一个新的矢量，比如F3，起点是第一个矢量的起点（F1的起点），终点是最后一个矢量的终点（F2的终点），那么这个新的矢量，就是其它首尾相连的矢量之和。

感觉太绕，直接上图说明一下吧：

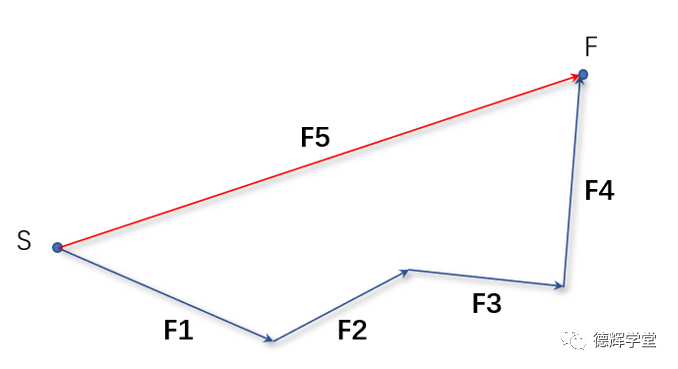
图7 矢量相加

图7中的矢量F1,F2,F3,F4就是首尾相连的矢量，红色矢量F5就是他们之和，即：

F5 = F1 + F2 + F3 +F4

相信很多数学基础比较好的小伙伴开始不耐烦，您在这里瞎咧咧半天，到底想说啥，和尺寸链计算有关系吗？

有关系的，在实际的公差计算中，F5代表封闭环，F1-F4代表的是组成环（也就是增环和减环的总称）。

我们在零件尺寸链，部件尺寸链，甚至整车尺寸链计算中，计算的其实就是矢量叠加！只是就一维的尺寸链计算来说，它是图7中的一种特殊情形，我们后边讨论。

在跳到下一个小节之前，我们先小结一下刚刚讲过的知识点：

     1. 矢量之和可以用三角形法作图表达，实际上就是多个矢量首尾相连叠加后的结果。比如图7中的红色矢量，它表达了矢量叠加的几何意义;

     2. 矢量可以用坐标表达，或者用代数表达，本质上是一样的。比如矢量F1既可以表达成F1=（3 , 4），也可以表达成 F1 = 3i + 4j ，（当然，本期文章用的2D的案例，3D的话，再增加一个Z坐标即可）;

     3. 矢量相加，实际上就是多个矢量对应的XYZ坐标分量分别相加。

     现在我们进入第二小节。

     2）矢量累加和尺寸累加

图7中显示的矢量累加的一般情形，在我们一般的尺寸链累加中，遇到更多的是一维的累加（或者，我们把它处理成一维的累加），它属于一种特殊情形。

它特殊在哪里呢？它特殊之处在于矢量之间的夹角θ。

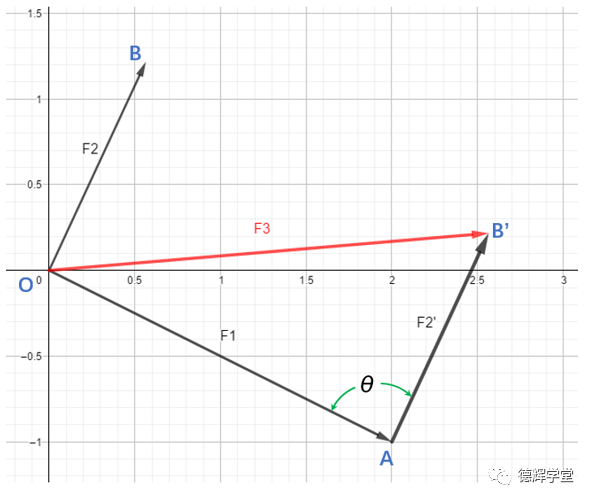
图8 矢量间的夹角θ

一般的计算中，我们遇到矢量间的特殊夹角一般是0°（组成环矢量的方向相同）或者180°（组成环的矢量方向相反）。

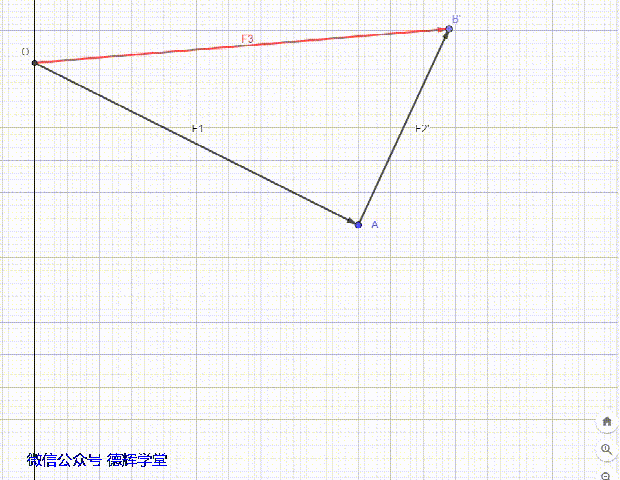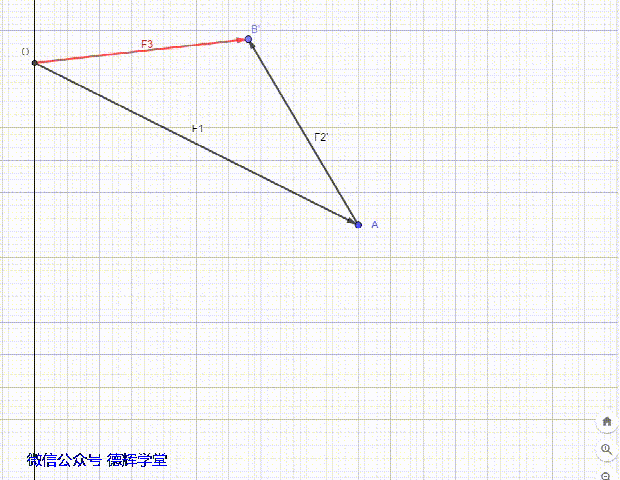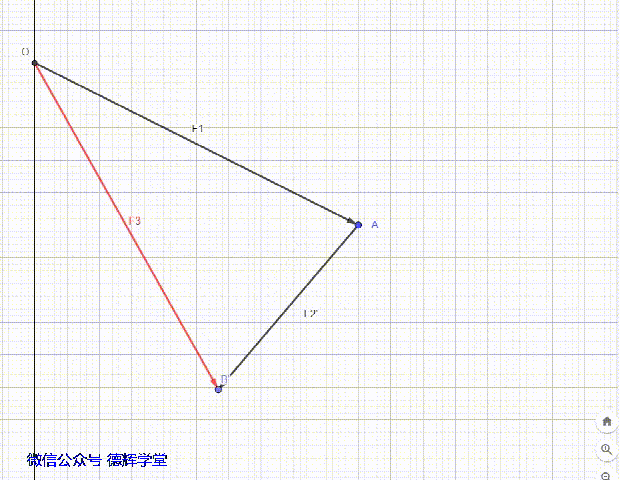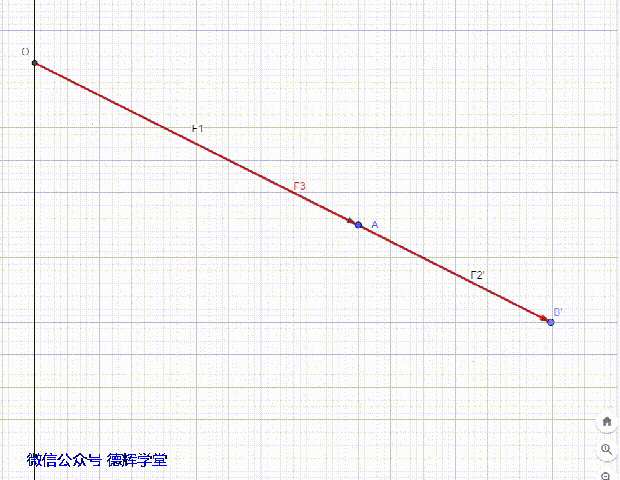
动画2 矢量间的夹角是0°

矢量间夹角是0°的情形见动画2。

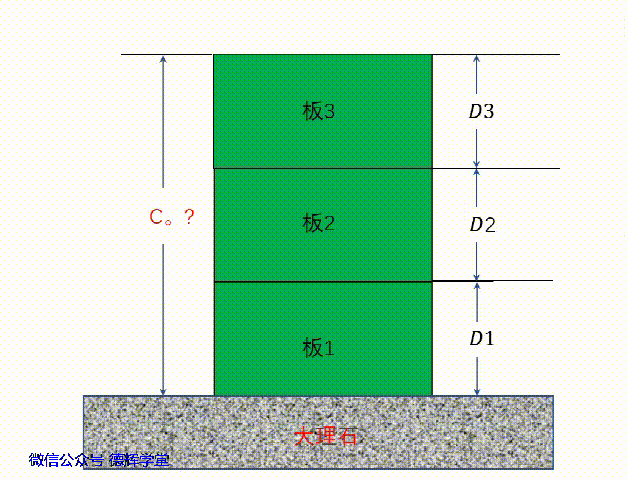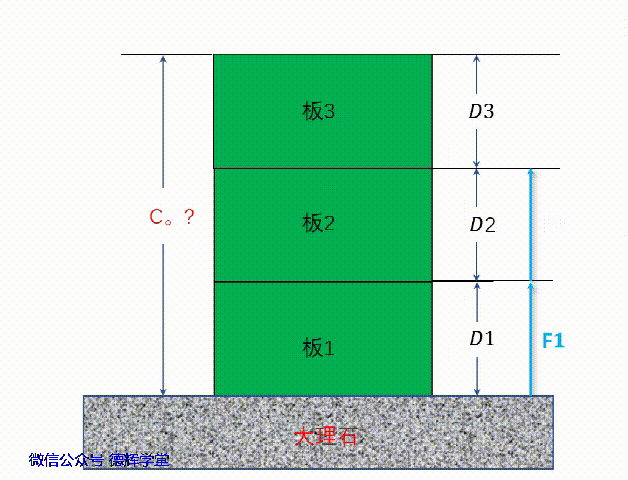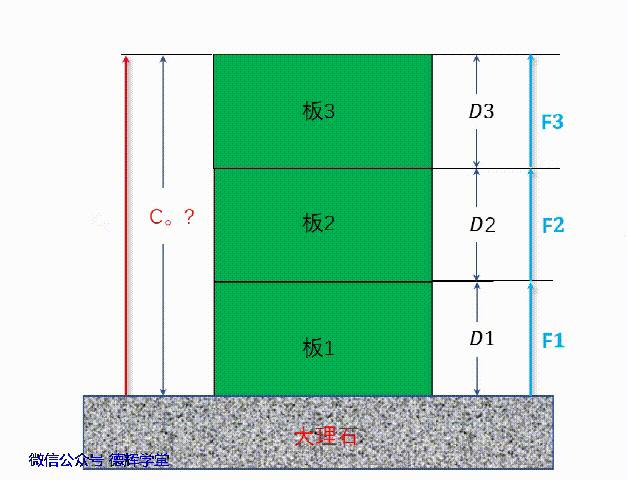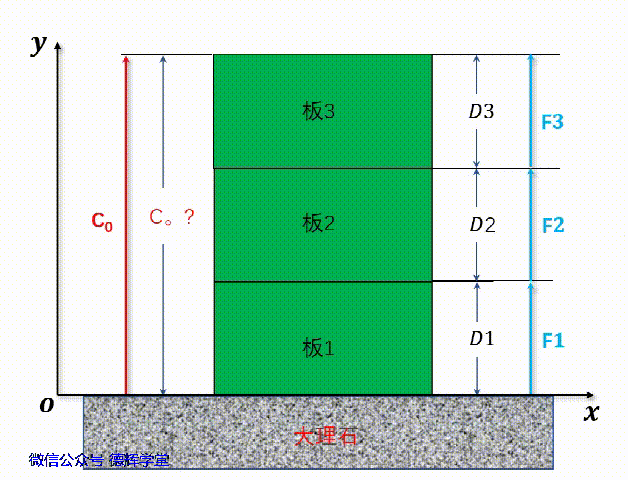
实际案例见图（9），已知板1，板2，板3每块板的厚度分别为D1,D2,D3, 求总厚度C_.0（不考虑形位公差）。

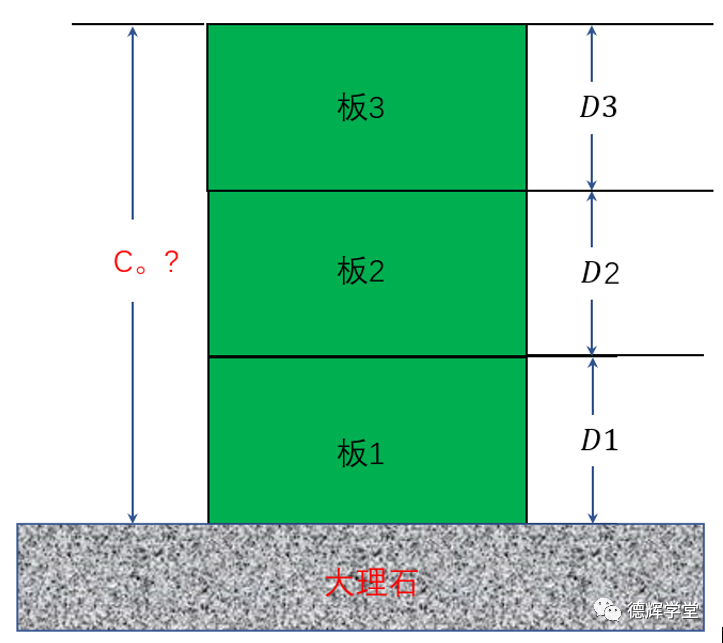
图9 计算3板总厚度

当然，如果不用所谓的矢量计算，我们可以用加法直接计算，显然有：

C₀ = D1 + D2 + D3   （3）

但是，为了用矢量来解释计算是否合理，我们再用矢量来计算一遍，先画矢量图，再建立坐标系：

动画3 建立矢量图和坐标系

动画3中建立的矢量图，组成环的矢量分别为F1, F2, F3, 封闭环的矢量为C₀, 我们分别将矢量F1, F2, F3这3个矢量的起始点移到坐标原点，便可以得到他们的坐标（显然，他们和Y坐标轴重叠）：

F1 = (0,D1) = 0i+D1j =D1 j

F2 = (0,D2) = 0i+D2j =D2 j

F3 = (0,D3) = 0i+D3j =D3 j

我们再假设C₀的坐标为（Cx, Cy）, 也就是C₀ = Cxi + Cyj

再将F1, F2, F3, C0同时移到Y轴，见动画4。

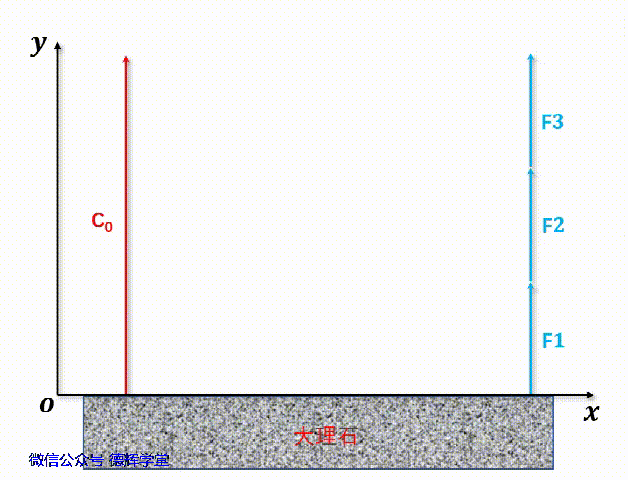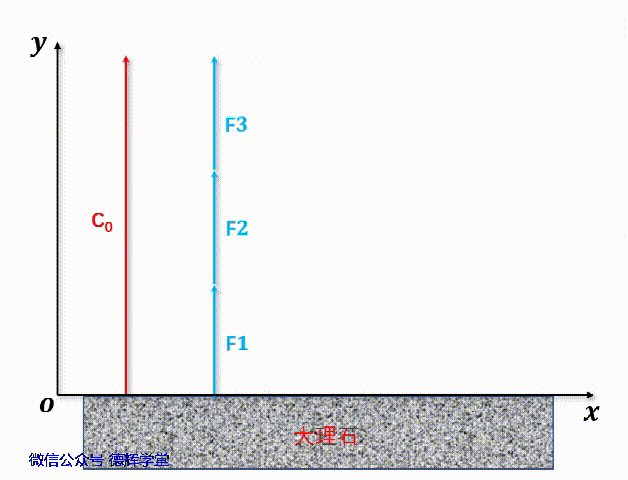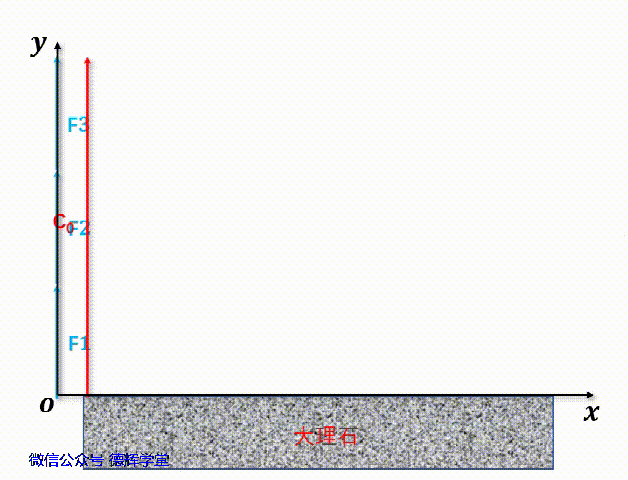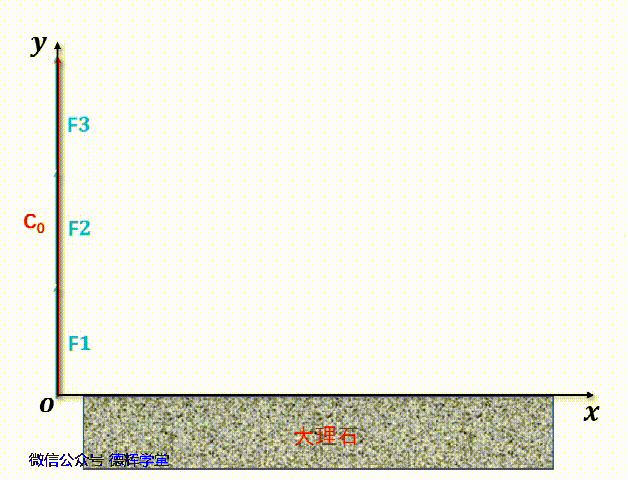
动画4 矢量相加

显然，根据动画4中的矢量表达，显然矢量C₀是矢量F1, F2, F3之和：

C₀ = F1 + F2 +F3

再代入每个矢量的代数式：

Cxi + Cyj = D1j + D2j + D3j

稍微整理有：

Cxi + Cyj = 0i + (D1+ D2 + D3) j

可以得出：Cx = 0 , Cy=D1+D2+D3

所以矢量C₀=(0,D1+D2+D3)=(D1+D2+D3)j

这时我们更加关心的三个板的高度，也就是矢量C₀的长度，所以有

| C₀| = D1+D2+D3     (4)

（这里就不在啰嗦勾股定理了，一条边的长度是0哦）

可以看出，按照矢量计算，和公式（3）计算的结果是完全一样的。

注意，图9中，没有减环，全是增环，所以根据公式（4），计算C₀的长度结果是各个组成环长度之和。

这里还需要强调一下，动画3中，我们在建立坐标系的时候，要特别注意，坐标系的原点一定要放在封闭环的一端，从坐标系原点指向封闭环的另外一端作为坐标轴的正方向，这样，封闭环的方向永远是正方向，这对封闭环计算结果的判断更加直观。

我们再来看另外一种情形，组成环之间的夹角是180°，也就是组成环之间的方向相反（首尾相连作为前提），这时会产生减环。见动画5。

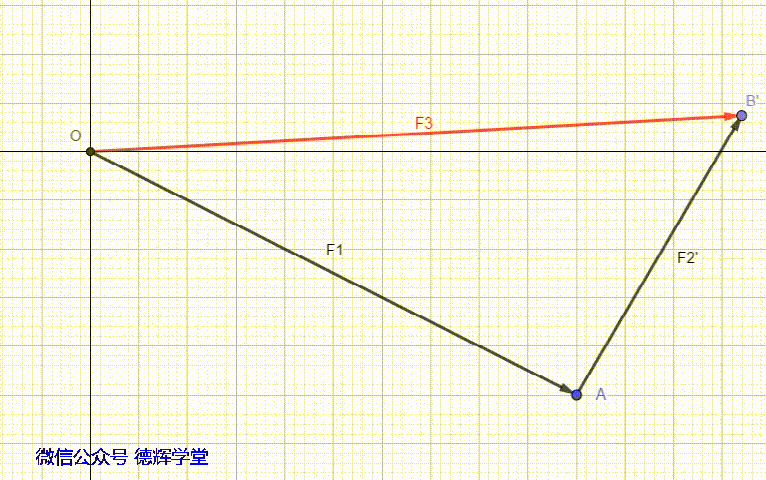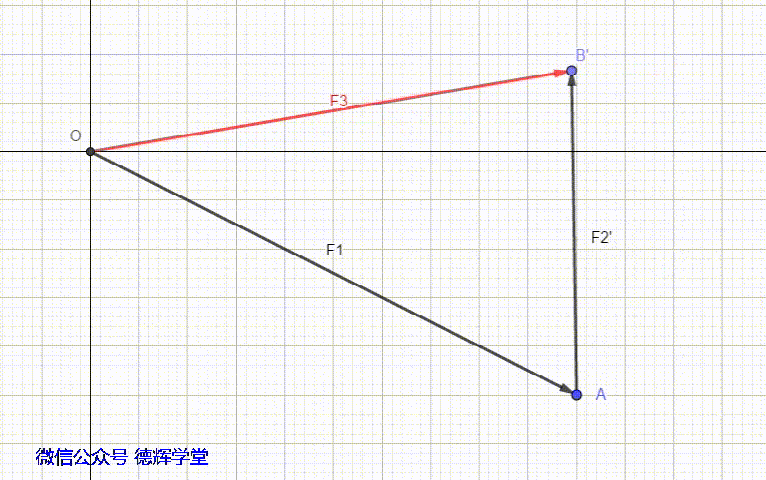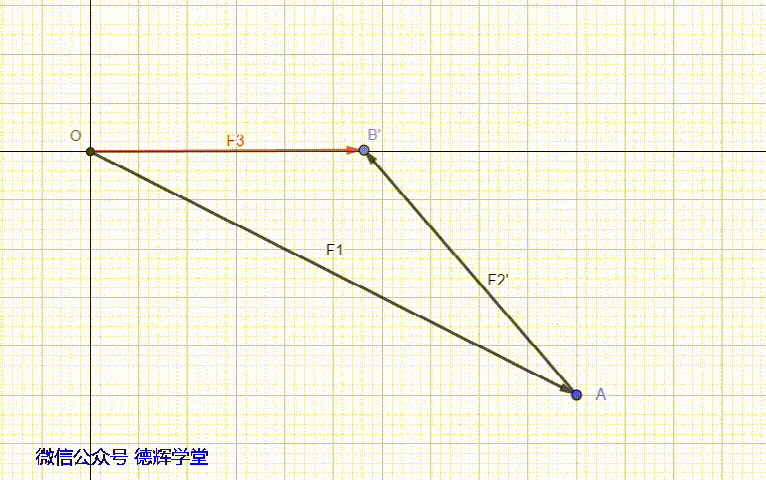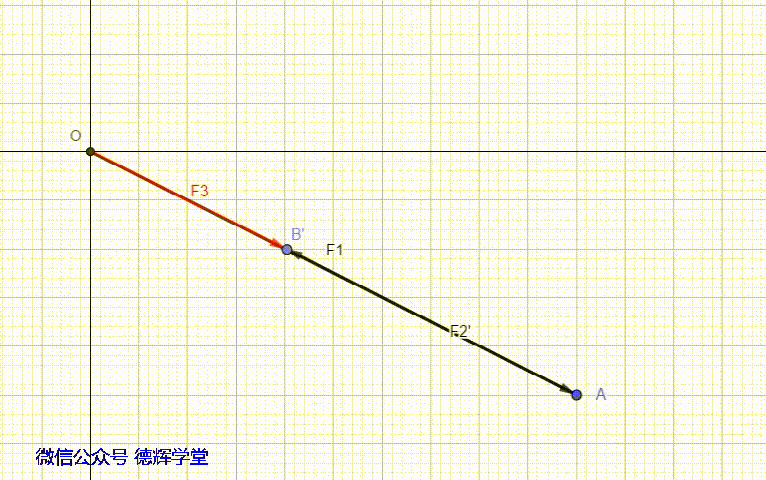
动画5 组成环之间的方向相反

本期文章的第一个案例就出现矢量方向相反的情形，见下面图9：

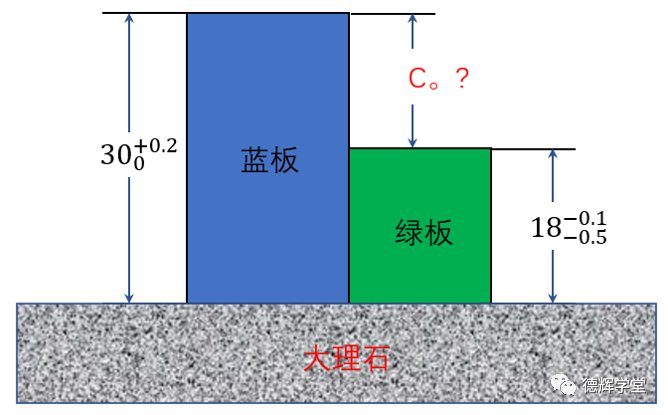
图9 求高度差

同样，我们建立矢量，建立坐标系：

动画6 矢量图建立

见动画6，将朝下的方向定义为y轴的正方向。所以，如果矢量D1和D2的起始点放在坐标系的原点O，可以分别得到D1和D2的矢量坐标：

D1 =（0, 30+0.2/0）= （30+0.2/0）j

D2 =（0, -18-0.1/-0.5）

     = -（18-0.1/-0.5）j

再将这些矢量移到一个数轴上，见动画7：

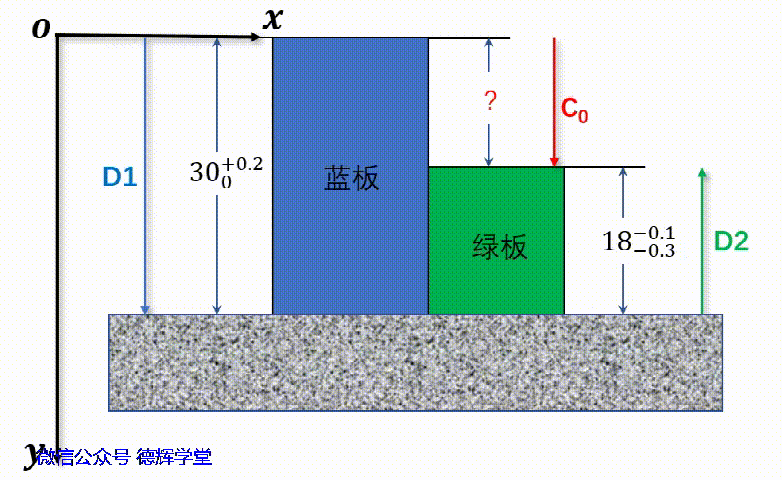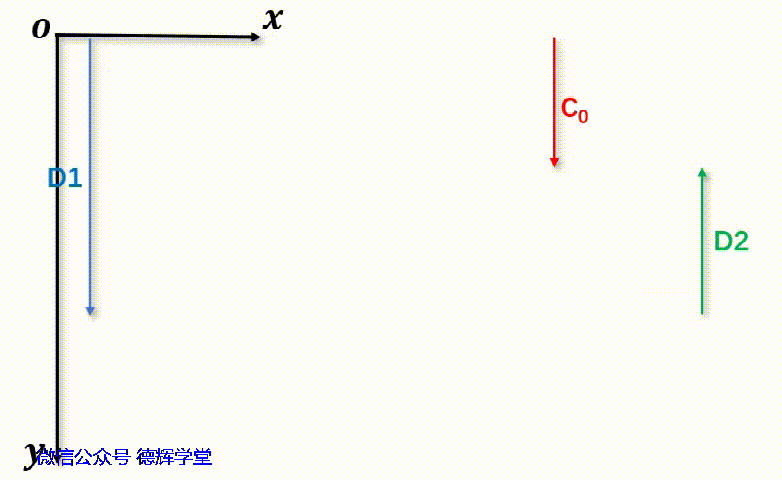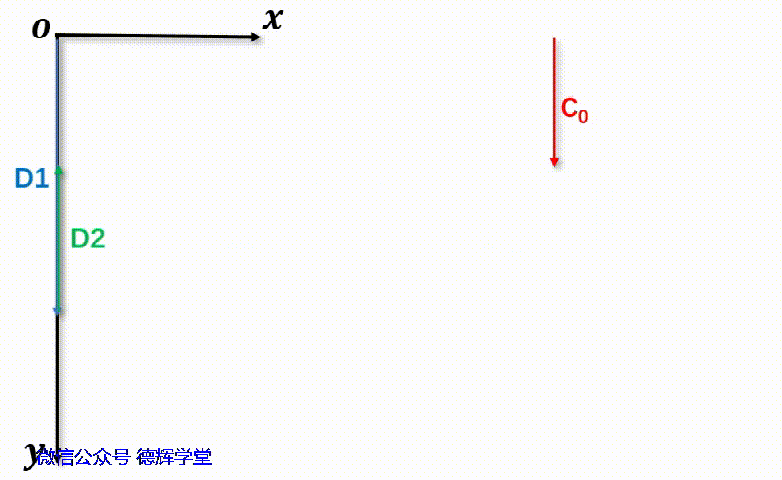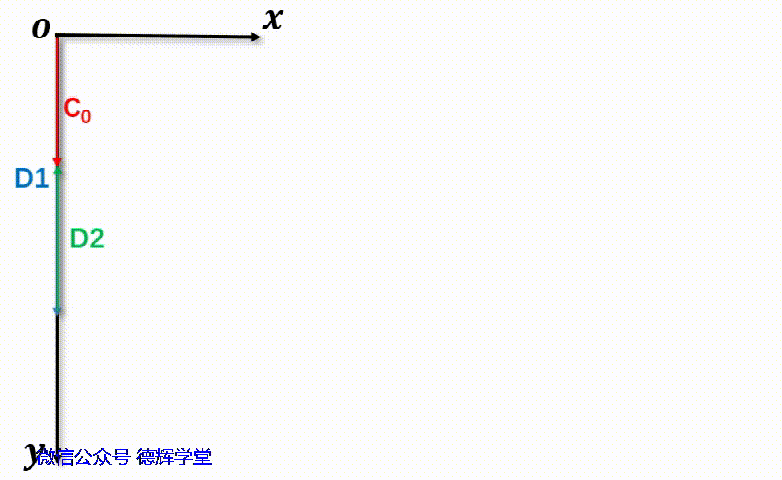
动画7 矢量相加

如果仔细观察动画7，发现D2的Y坐标值是负值。如果还不理解，看下面这个动画8，注意，坐标轴朝下是正方向哦。

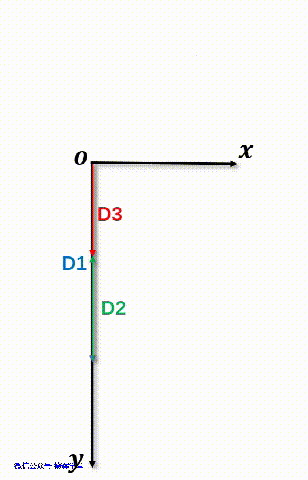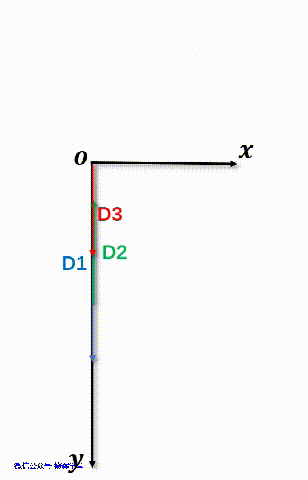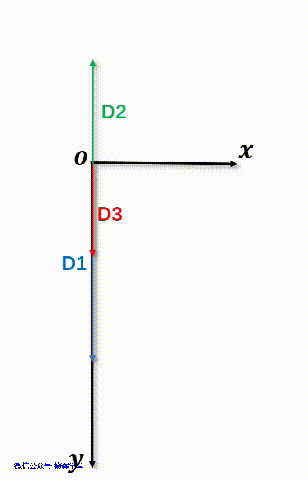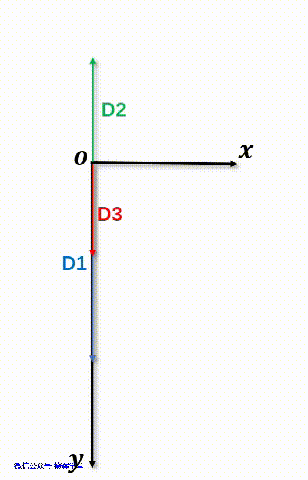
动画8 向量D2的坐标

从动画8中可以看出，D2的方向，和封闭环的方向是相反的，所以，它是一个减环。

另外，我用带公差的数值来表达坐标，大家不用感到意外，就把它看成一个数就OK了，后边我们会用区间法再来分析。

根据动画:7中的矢量关系，显然有：

C₀ = D1 + D2 

     =（30+0.2/0）j +(-(18-0.1/-0.5）) j

     =(（30+0.2/0）-（18-0.1/-0.5）) j

封闭环矢量知道了，我们可以轻松算出C₀的长度：

|C₀| =(30+0.2/0)-(18-0.1/-0.5) （5）

再一次强调，建立坐标系的重要性（见动画6），将坐标系原点放在封闭环的一端，坐标原点指向封闭环的另外一端作为正方向，这样使得封闭环的方向在坐标系里边，永远是正的。而且，在组成环的矢量里边，正方向的矢量就是增环，负方向的矢量就是减环。

当然，归根结底，见公式（5），我们纠结增减环的目的，主要是为了方便在计算封闭环的时候，应该采用加法还是减法。

结果很明确，增环用加法，减环用减法（因为它的坐标值就是负的）。

到这里，第一章节就结束了，还是小结一下，本节啰里啰嗦半天，就说明以下内容:

     1. 任何尺寸链的计算，都可以用矢量和来表达，也就是可以用首尾相连的矢量图来表示，组成环就是这些矢量，而矢量之和就是封闭环。

     2. 对于一般的线性尺寸链，大部分是单维度的（一维），要么只有X轴的分量，要么只有Y轴的分量，这些分量的大小就是具体的尺寸，所以计算起来非常简单。

     3. 因为尺寸链必须表达成首尾相连的矢量和，在一维的尺寸链里边，有可能组成环之间的矢量方向会相反，这样就会产生减环。

     4. 判断增减环的方法，和建坐标系有关系，一般的建议是，把封闭环的方向设置成坐标轴的正方向，然后看组成环的方向，和封闭环方向相同的是增环，相反的就是减环。当然，在计算的时候，增环用加法，减环用减法。

 2.    区间分析和公差累加

我们前面讲过，如果将尺寸公差转化成对称公差后，尺寸部分增环用加法，减环用减法，而公差部分，永远用加法。

公差部分，为啥永远用加法呢？对它的这种处理方法是否有数学依据？

当然有，我们先来了解区间分析，然后再来看公差累加。

     1）区间数学的基本知识

区间这个概念，高中学函数时就接触过，我们确定定义域的范围，值域的范围的时候，就会用到区间（高考出题者经常会卑鄙的用这招来考我们）。

简单举个例子，如X∈[2, 8]，它表达的就是区间(2≤X≤8)，表示X是一个从2到8之间的实数，比如X可以是2，2.4, 5，7 等等。

区间数学，它其实是数学的一个分支。基于区间数学的分析，叫区间分析（Interval Analysis），它最早是在1966年由 Ramon E. Moore出专著提出。

慢点，为啥我们要扯区间分析这种学术性的东西？

因为公差(Tolerance)，不管是尺寸公差，还是几何公差，它本身是不是就是一个区间啊？

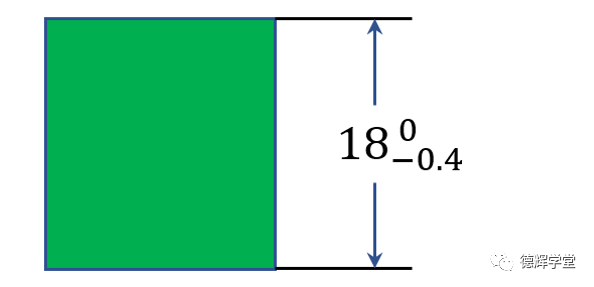
图10 板的高度公差

比如图10中，板的高度是由客户的设计工程师规定，而供应商加工出来的实际零件，在合格的情况下，设它的实际高度为X，X具体是多少，谁也说不清，但是我们知道它所在的区间（不考虑形位公差），即：

X∈[17.6 , 18]

同志们，所有的零件，在测量之前，其实我们都不知道它的具体尺寸是多少，我们只知道它的区间。而我们苦逼的设计工程师，尺寸工程师，每次要计算的，不是将几个具体的数值简单的累加起来，而是在对几个区间进行累加。

所以，公差分析，实际上就是区间分析！

区间分析的内容很多，我们还是只捞出和线性公差累加相关的知识点来吧。

     1. 区间的加法

如果 X = [ a , b ] ， Y = [ c , d ], 那么有：

X+Y = [ a+c , b+d ]

这个应该好理解，两个尺寸公差相加的时候，上限加上限就是上限，下限加下限就是下限（我假想您知道我在说什么）。

当然，上面的定义要完善一下，比如，X,Y, a, b, c, d都属于实数R，而且a≤b, c≤d。

举个例吧，比如：X = [ 9 , 10 ] ， Y = [ 5 , 6 ]，那么有：

X + Y = [ 14 , 16 ]

     2. 区间的减法

如果 X = [ a , b ] ， Y = [ c , d ], 那么有：

X-Y = [ a-d , b-c ]

这个也应该不难理解，下限减去上限就是下限，上限减去下限就是上限。有点绕，但是相信您也知道我在说什么。

严谨起见，同样有X,Y, a, b, c, d都属于实数，而且a≤b, c≤d。

同样，举个例吧，比如：X = [ 9 , 10 ] ， Y = [ 5 , 6 ]，那么有：

X - Y = [ 3 , 5 ]

     3. 区间的中点和宽度

如果有 X = [ a , b ]，那么该区间有中点m(X)和宽度w(X)

m(x)=(a+b)/2,  w(x)=b-a

这个也不难理解，比如尺寸公差10^+0.2₀，它的中点就是m(x)=10.1，宽度w(x)=0.2, 也就是公差。

这一点，您在将尺寸公差转化成对称公差的时候，是不是很熟悉？

     4. 点区间和对称区间

如果有X = [ a , b ]，其中a=b, 那么X所在的区间就是点区间，实际上就是一个点(或者一个数)了。即：

X = [ a , a ] = a

如果有X = [ -a , a ]，（其中a>0）, 那么X所在的区间就是叫对称区间。对称区间最大的特点是，两个对称区间相加和相减的结果居然是等同的(这个有点罕见哦)。

比如 X = [ -a , a ], Y = [ -b , b ], （其中a>0,b>0），那么我们利用区间的加法和减法计算，不难得出：

X + Y = [ -a-b , a+b ] =（a+b）[-1, 1]

X - Y = [ -a-b , a+b ] =（a+b）[-1, 1]

看到没有？对称区间的加法和减法的结果是相同的。

另外，我们把 [-1, 1] 叫单位对称区间，它前边的系数a+b叫区间半宽。

对上面的案例，我们再做一个推演（这样就越来越靠近公差累加了）。

因为X = [ -a , a ], 可以转化成:

 X =a[-1, 1]   (6)

其中a就是区间半宽（a>0）。

又因为Y = [ -b , b ], 可以转化成:

Y =b[-1, 1]   (7)

其中b就是区间半宽（b>0）

将一个对称区间的格式写成（6）和（7）样式，半宽和单位对称区间的乘积，这样的格式我们取名叫标准对称区间。

标准对称区间的特点是，无论是相加或者相减，它得到的结果都是半宽系数之和再乘以单位区间。如下：

推论1：多个标准对称区间之间的和或者差，等于他们的半宽之和乘以单位对称区间。

假设有X =a[-1, 1] , Y =b[-1, 1], Z =c[-1, 1], (其中a>0,b>0,c>0)，那么有：

X+Y-Z = (a+b+c) [-1, 1]

X-Y+Z = (a+b+c) [-1, 1]

推论2：对于任何一个区间X∈[ a, b ]，都可以写成区间中点（或者点）再加上一个标准对称区间，它的这种格式，我们把它叫区间的对称格式。即：

X = [ a, b ] = m(x)+w(x)/2[ -1, 1 ] 

   = (a+b)/2 + (b-a)/2[ -1, 1]   （8）

其中，区间中点m(x)=(a+b)/2, 区间宽度w(x)=b-a.

推论2的公式看起来有点复杂，实际上很简单，也很容易证明：

X=(a+b)/2 + (b-a)/2[ -1, 1 ] 

= [ (a+b)/2, (a+b)/2] + [ -(b-a)/2,(b-a)/2]

= [ (a+b)/2-(b-a)/2,(a+b)/2+(b-a)/2]

= [ a, b ]

上面的证明，包括公式看起来有点眼花缭乱的样子，事实上，您如果计算过尺寸链，要把某个尺寸公差转化成对称公差，您肯定自觉或者不自觉的用过上面的推论2。

推论2理解起来很很简单，站在尺寸公差的角度，就是说，任何尺寸公差都可以表达成对称公差。

是不是So easy?

     2）区间分析和公差累加

前面讲了半天，和公差累加有关系吗? 当然有！因为：

区间 = 公差

比如尺寸公差D=10₀^+0.2， 如果写成区间形式，则为：

D = [ 10, 10.2 ]

根据推论2，如果将D的区间格式写成对称格式，则为：

D =10.1 + 0.1[ -1, 1 ]     (9)

如果将尺寸公差变成对称公差：

D = 10.1±0.1   （10）

比较一下公式（9）和公式（10），是不是很相似？实际上它们本质是一样的，见图11中表达的对应关系：

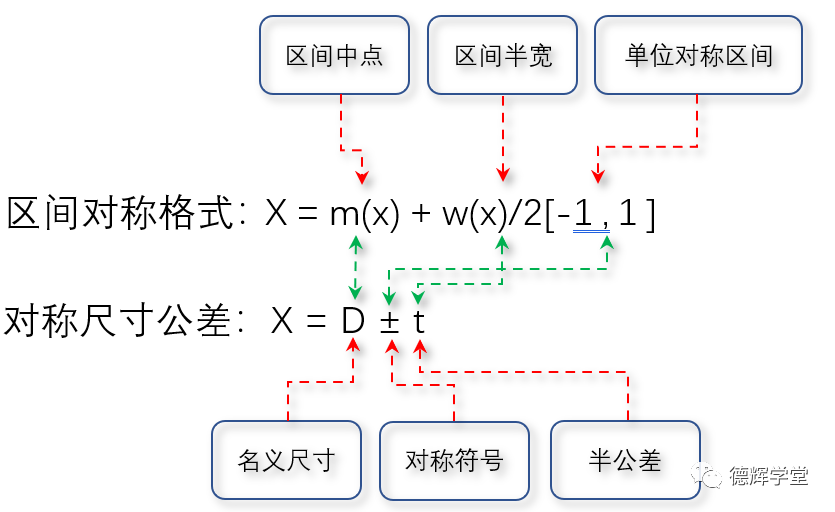
图11 区间对称格式和对称尺寸公差的对应关系

好了，我们现在知道了区间分析的一些特点，也知道了尺寸对称公差和区间对称格式之间的对应关系，我们在计算尺寸链的时候，根据区间分析的特点，就可以灵活处理尺寸部分和公差部分了。

比如，在一个线性一维的尺寸链里边，有三个尺寸环（组成环）, X1=D1±t1, X2=D2±t2, X3=D3±t3, 在矢量图里，X1, X2是增环，X3是减环，求封闭环C₀?

这里不考虑矢量图，我们直接考虑数据的计算部分，显然有：

C₀ = X1 + X2 – X3

  = (D1±t1) + (D2±t2) – (D3±t3)

注意，上边的计算实际上就是区间的加法和减法计算，D1, D2, D3可以看成点区间（实际上就是一个点, 或者一个值），把它们一起处理，处理起来也很容易，直接加减就OK， 而±t1, ±t2, ±t3则是对称区间，根据对称区间的特点，不管是加减，都是将半宽之和直接相加。所以有：

C₀ = (D1±t1) + (D2±t2) – (D3±t3)

  =（D1+D2-D3）±（t1+t2+t3）

您，看明白了吗？

还是综合举一个案例吧，已知装配关系和零件尺寸如图12所示，要求δ的变化范围（不考虑形位公差）。

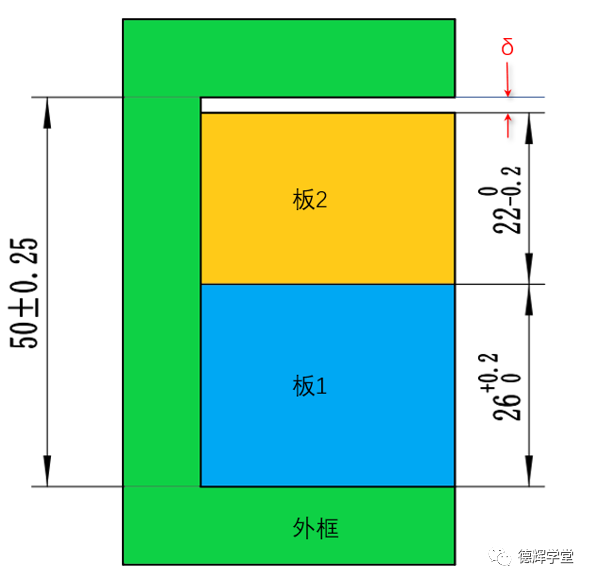
图12 综合案例

图12中，板2和外框之间的缝隙δ是封闭环，要计算它的大小，根据第一章讲的，建立坐标系，画出矢量图，见下图：

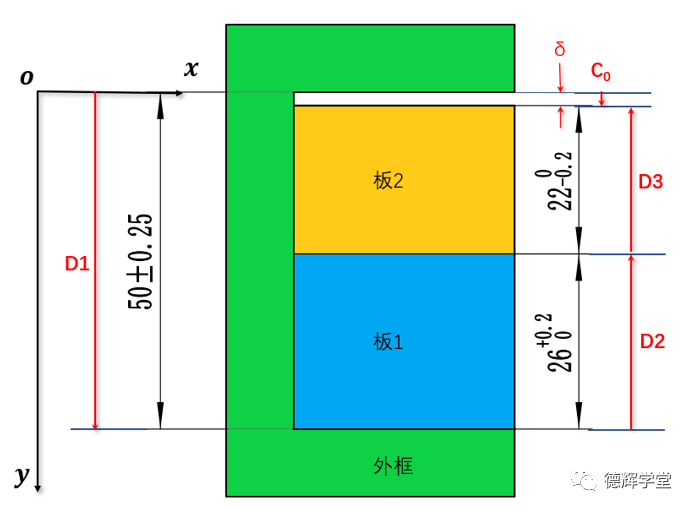
图13 矢量图

根据图13的矢量图，显然有：

C₀ = D1 + D2 + D3

其中每个矢量的坐标为:

D1 = ( 0, 50±0.25 ) =（50±0.25）j

D2 = ( 0, -26₀^+0.2) = -(26₀^+0.2) j

D3 = ( 0, -22⁰_-0.2) = -(22⁰_-0.2) j

所以可以得：

C₀ = D1 + D2 + D3

 =（50±0.25）j - (26₀^+0.2) j - (22⁰_-0.2)j

=（50±0.25 - 26₀^+0.2  - 22⁰_-0.2）j

最后可以得出：

δ = |C₀| = 50±0.25 - 26₀^+0.2  - 22⁰_-0.2

显然，δ是一个区间，要算出δ的大小，就是要处理区间分析的问题了，根据我们前面讲的知识点，先将尺寸公差处理对称公差，然后利用推论1，则有：

δ = 50±0.25 – 26.1±0.1– 21.9±0.1

  =（50-26.1-21.9）±（0.25+0.1+0.1）

  = 2 ± 0.45

当然，也可以用EXCEL表格计算，如下：

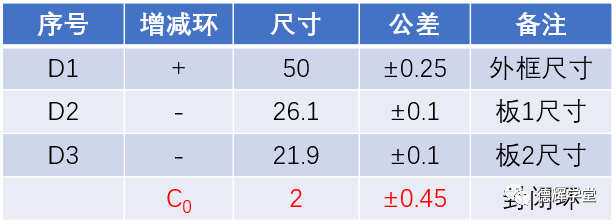
图14 尺寸链计算表格

您理解了吗？

好了，本文到这里就结束了，希望对您有所启发。

本文小结

本期文章探讨的是基本的线性一维尺寸链计算，它背后的数学原理，或者说理论依据。

第一章节，我们介绍了矢量的基本概念，然后介绍了尺寸链实际上就是矢量累加，因为每个封闭环都可以表达成矢量和的形式。当然我们又介绍了，如何取得每个矢量的坐标值，或者代数表达式，要注意的是，减环的矢量坐标是负值。

第二章节，我们介绍了区间分析的基本知识；然后指出，公差累加，实际上就是区间累加，而且我们介绍了标准对称区间，以及区间的对称格式，以及它们累加时的特点；最后指出，对称的尺寸公差，实际上就是区间的对称格式。

最后我们用一个简单的案例，综合回顾了第一章节，第二章节知识点的应用，证明了常规计算尺寸链方法的合理性。

【后记】

      本期文章的目的，本质上是在为我们平时计算尺寸链累加所用的方法寻求理论依据，证明其合法性。相当于强行扯过来一顶光鲜的帽子戴在头上，表示其光鲜。

尽管帽子是临时扯过来，大小却是合适的。

企业工程师计算尺寸链累加所用的方法，似乎是口口相传，很少有人思考后边的理论依据。如果我们所用的方法，缺乏理论依据，其实是危险的，有可能在某些特殊情况下，我们的方法就不能使用了，这可能会闯祸的。

我在上课时，也被工程师们质疑过，很是惭愧，我之前也没有系统思考过这个问题。不过这次趁春节假期，被疫情困在家里，梳理了一下后边的原理。

我是用矢量和区间分析来解释我们计算尺寸链的方法。相信不是唯一的理论依据，有兴趣的小伙伴，也可以思考其它的理论依据。

如果觉得文中理论有问题，欢迎随时给我留言哦。

参考资料：