大半径小圆弧，是一个永恒的测量问题，用什么样的方法测量最准确成为了业界争执不下的千年无解方程式。今天，我们将围绕以下几个问题展开研究，看看是否真的无解。

1、什么叫做大半径小圆弧？

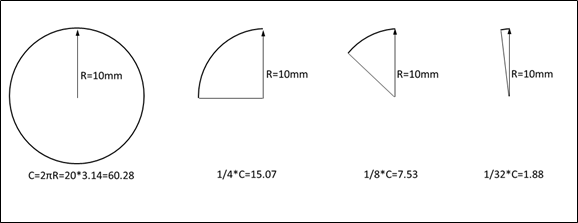
如上图，当弧长小于1/4周长C的时候，我们统称为大半径小圆弧，当弧长远远小于半径时，比如弧长等于1/32周长，要通过测量该小段圆弧确定半径R，这个测量过程会产生巨大的半径偏差。

2、大半径小圆弧的测量不确定性到底有多大？

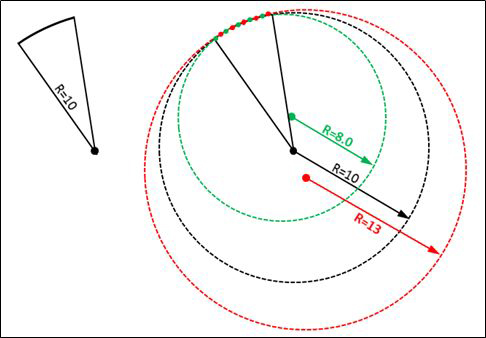
如上图，要检测一个只有15°的圆弧，半径为R10，使用OMM测量5个点构造圆弧输出半径，这个时候红色点和绿色点之间只错位了一个点位置，测试结果却产生了巨大偏差。

我们再举一个实际案例。假设小于1/4圆周（<90°）的圆弧角度为66°，理论直径为2.10+0.08/-0.03.

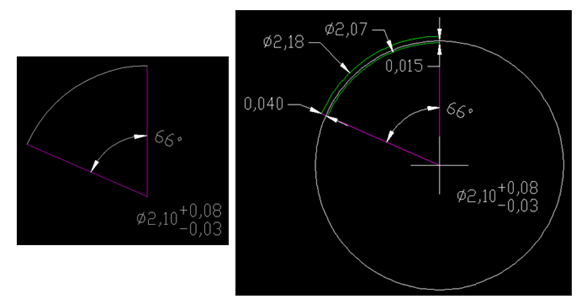
第一种状态：

假设圆心无偏移。通过理论圆心分别标出上限2.18和下限2.07，这个时候圆弧的半径正偏差是0.04，负偏差是-0.015。也就是说，假设圆心在实际测量中不会发生偏差，那么这个测量公差带可以在0.04+0.015=0.055这个范围内波动，这个偏差理论上设备是完全可以满足的。

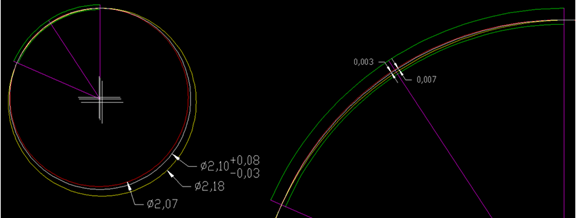
第二种状态：

但是在实际测量活动中，圆心一定会发生偏差。通过作角平分线，假设圆弧两端部无任何偏差，此时经过角平均线上的半径偏差最大，这样，经过圆弧两端点分别作2.18和2.07圆，我们发现，经过角平均线上的正偏差为0.003，负偏差为-0.007。

这说明了假如圆在2.10+0.08/-0.03范围内变动，并且圆弧两端部无任何变动的情况下，角平均线上允许的最大偏差只能控制在+0.003/-0.007范围内，而在实际测量中，圆弧两端的点、角平均线上的点以及圆弧其他任何位置上的点都会产生不同程度的变动，我们假设这些点都在0.005+0.005/-0.005范围内变动，虽然这个变动非常接近测量设备的极限精度，但是，所有变动点构造成的圆弧一定是产生大偏差的。

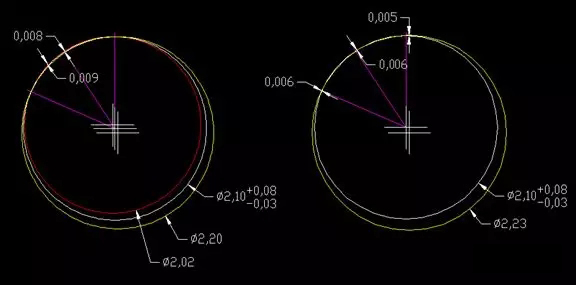
如上图，所有测试点都在μ级以内偏差，但是圆直径已经超差+/-0.05，这充分说明了大半径小圆弧的测量是不准确的，并非测量设备问题，而是大半径小圆弧的特征限制了其并不具备准确测量的资格。

类似大半径小圆弧的测量，最理想的公差设定方式应该是根据零件实际装配需求，转换成带基准的线轮廓度。

比如以上案例中，假设实际装配需求是圆弧的每个点允许偏差为+0.04/-0.015,那么排除参考基准的公差累积，转换为线轮廓度则为0.055U0.04，相对于设备μ级的变异，这样的公差是完全可以准确控制的。

3、为什么现在的设计图纸都要求管控这些圆弧？

因为对于异形零件，在组装公差配合要求越来越高的市场需求下，圆弧与圆弧之间的配合非常频繁，设计图纸是不可避免的需要管控圆弧尺寸，而现在的图纸设计者设计水平参差不齐，尤其是对GD&T理解欠缺的前提下，设计者往往会趋向于直观标注尺寸的思路，忽略了零件之间实际配合公差的要求。

4、目前到底有哪些测量方法可以解决大半径小圆弧的相对准确测量？

（1） 通过参考零件基准坐标系，偏移间隔相等的点，定点测量；

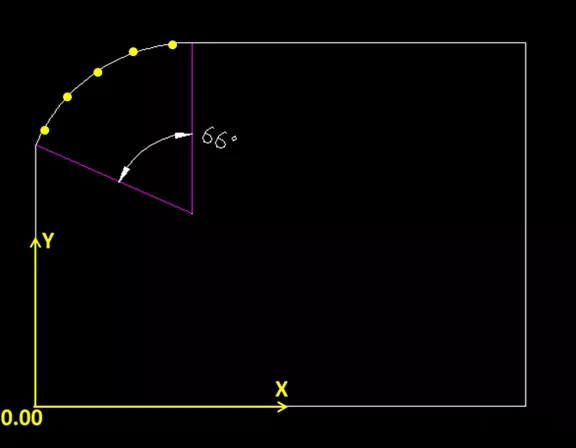
优点：

可以保证每个点都有固定的坐标，确保测量的一致性；

缺点：

当基准坐标不稳定、或相对于基准坐标的纵横向距离尺寸公差比较大时，会导致所定的点脱离了圆弧的实际范围，或者所定的点并非覆盖到圆弧的80%实际圆弧上，这样就会产生巨大偏差。

（2）在影像测量仪中，参考基准坐标系，把基准原点平移到圆弧所在的理论圆心，再把直角坐标XYZ切换为极坐标RθZ，接着在圆弧任意位置取多个点，选取半径偏离理论半径最差的值作为最终测量值；

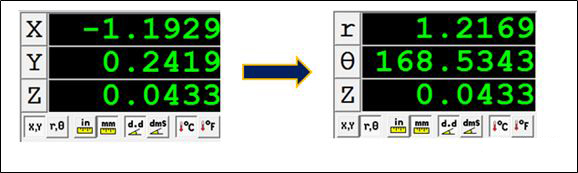
优点：

不用考虑基准的偏差累积，该方法可以准确的测量圆弧的半径偏差；

缺点：

该方法需要频繁切换坐标系，并且需要目视手动或半自动取点，效率低下，只适合于做工程开发检测验证，不适合制程检测。

（3）如果与圆弧相切的边缘都是直边，可以直接运用该两条直边的交点作为坐标原点，再偏移间隔相等的点，定点测量；定点的同时，要始终确保所有点的X或Y坐标一定不是0，这样就能最大限度的确保点落在圆弧范围内。

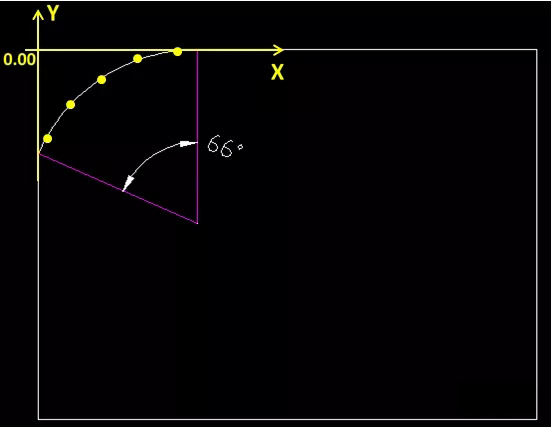
优点：

该方法消除了基准坐标系、相对于基准坐标系的线性距离公差的累积误差。

缺点：

当与圆弧相接的两直边直线度较差，并且端部发生变形时，取线的长短直接影响圆弧的准确测量。解决方案就是通过基准坐标系，定义线的起始位置，确保测量线段的一致性，最大限度的控制圆弧上的测试点的稳定性。

（4）通过KEYENCE一键式测量设备的直线和直线自动构造切点圆弧功能，直接读取圆弧半径；

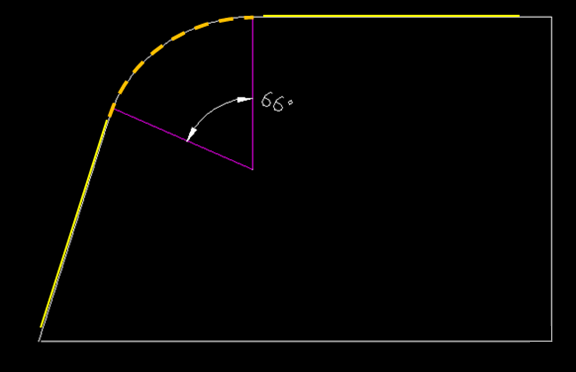
优点：

避开了直接取圆弧带来的不确定性偏差，重复性好；

缺点：

无（只适用于与圆弧相切的直线边缘非常规则的产品）

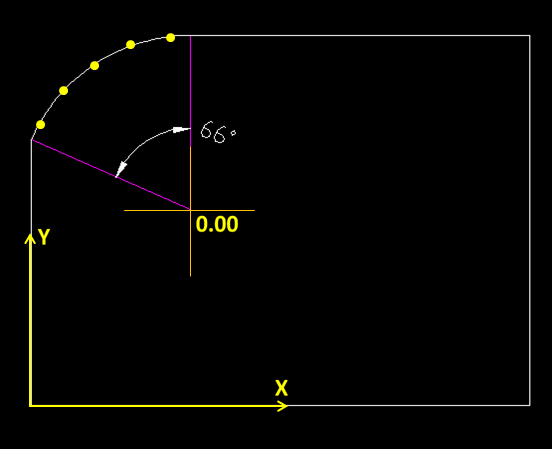
（5）参考基准坐标系，把基准原点平移到圆弧所在的理论圆心，再以理论圆弧中心为原点，等分固定角度旋转坐标系，在圆弧上相对于坐标系的X或Y的零点上取点测量。

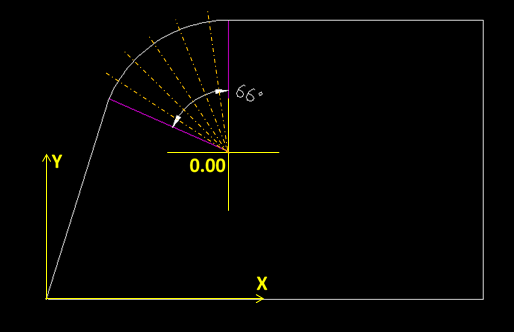
优点：

可以确保所有点的方向一定是在每个旋转坐标系的0点位置，重复性好；

缺点：

当实际圆弧范围远比理论圆弧范围大或小很多的时候（假设圆弧半径OK），该方法无法准确测量，该方法适用于CNC精加工零件的检测。

总结

对于大半径小圆弧的测量，其测量方法还有很多种类，不管使用任何方法，都有一定的局限性，需要做到具体问题具体分析后，再选择最佳测量方案。

在实际的工程图纸评估中，我们提出更改为线轮廓度管控的同时，要懂得运用GD&T基础知识，结合实际装配需求，定义出具体的线轮廓度公差。