数与形，本是相倚依，

焉能分作两边飞。

数缺形时少直觉，

形少数时难入微。

数形结合百般好，

割裂分家万事非。

-----华罗庚

【前言：我们在推出上一篇文章《基准偏移和坐标变换》之后，收到不少小伙伴的反馈和提问，有小伙伴反馈说文章中的数学内容有点晦涩难懂。刚好，来自一汽的尚工，他提出了一种比较容易理解的数学方法计算位置度，他的思路是将被测要素放到基准坐标系中，计算出被测要素在基准坐标系中的坐标，再来计算被测要素到理想要素的距离，最后乘以2。他的计算过程整个思路清晰，逻辑合理，所谓条条大路通罗马，这里把他的文章分享给大家！】

***************************************

    我们要解决的问题如下，一致图纸标注如图1标注：

图1 图纸标注

    已知在三坐标坐标系下测得圆孔坐标为PB（37.36，33.51），PC（77.21，36.95），PD（56.31，52.59），见图2。求被测孔PD的实测位置度（图1红圈处）？

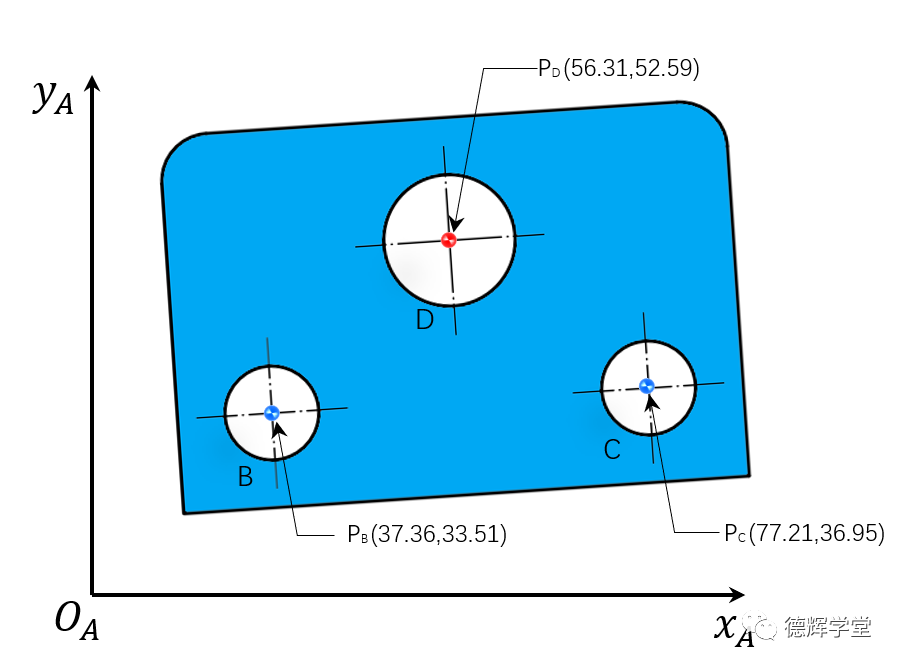
图2 在机器坐标系中3个孔的坐标

    现在工件上以B基准为原点，以BC基准连线为X轴，建立工件坐标系，评价D的位置度。

    先说一下，要用到的基本数学知识                         

来看一下计算过程：

1. 连接BC，根据两点确定一条直线，建立直线方程L1, 见图3：

   
   

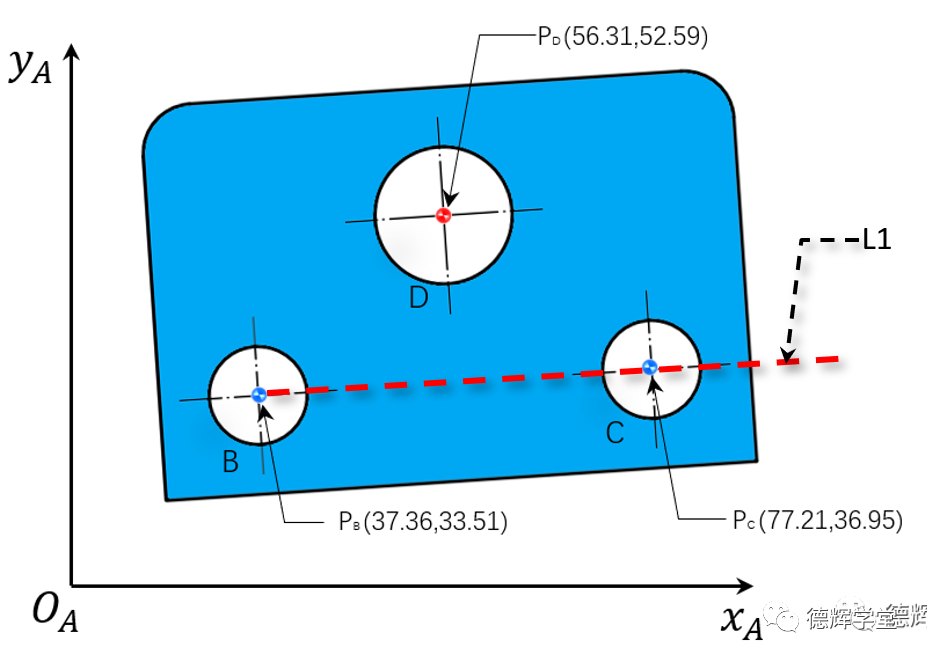
图3 建立直线方程L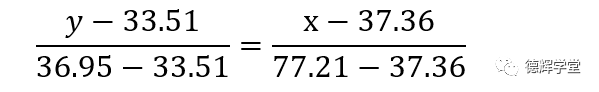1

 （1）

整理可得L1的方程式为：-3.44x+39.85y-1206.8551=0

    2. 计算点PD到直线L1的距离：

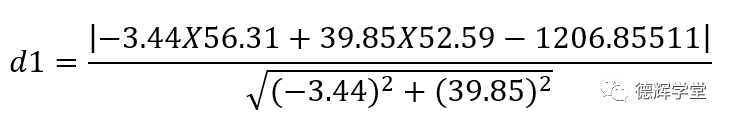    （2）

整理可得：d1=17.3795，见图4

图4 被测要素到L1的距离d1

    3. 将直线L1绕点PB旋转90度。可得直线方程L2.

B（x-x0）-A（y-y0）=0

39.85（x-37.36）-（-3.44）（y-33.51）=0

    整理可得L2的方程式为：39.85x+3.44y-1604.0704=0

图5 建立直线方程L2

    4. 计算点PD到直线L2的距离：

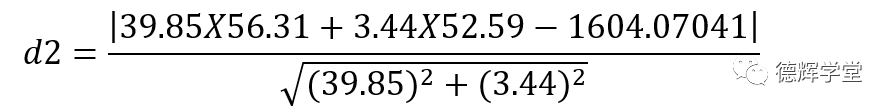
    整理可得：d2=20.52074031，见图6

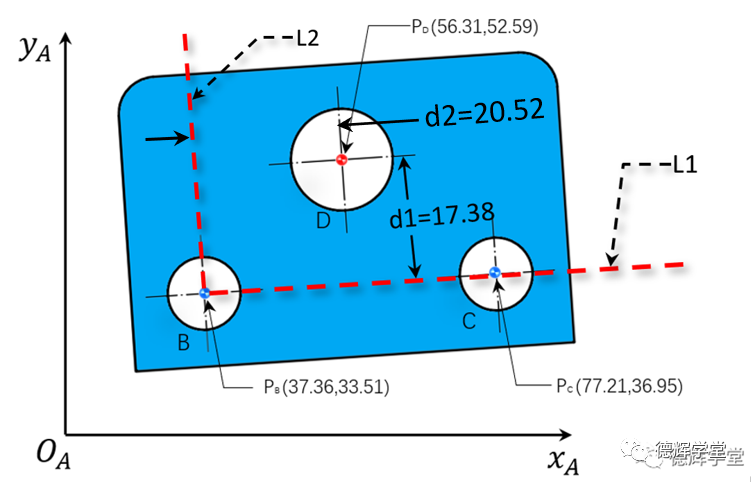
图6 被测要素到直线L2的距离d2

    以上计算出来的d1和d2，实际上就是点PD在基准坐标系中的XY坐标了，其中，X=20.52,Y=17.38。

    现在我们已经知道了PD的实际坐标，而且也知道理想要素P的坐标（20,17），再来计算位置度就非常容易了。

    5. 计算位置度：

    约等于1.289，计算完成!

***************************************

    最后，留一道思考给您，见图7：

图7 带角度的基准系

    如图7所示标注，C基准与B基准成一定角度。假设我们已知基准要素B上的两点PB1和PB2(该两点距离距离较远，且和A不垂直）， 而且还知道基准要素C上的一点PC1, 根据这个已知条件，那么我们应该如何构建该零件的基准坐标并计算出位置度的几何误差？

    如果您有兴趣，欢迎您把您的处理方式发给我们哦！

相关知识：

1. 求过已知点与已知直线平行的直线方程

定理1 过点M（x0，y0）且与直线Ax+By+C=0（其中A²+B²≠0）平行的直线方程是A（x-x0）+B（y-y0）=0

2. 求过已知点与已知直线垂直的直线方程

定理2 过点M（x0，y0）点且与直线Ax+By+C=0（其中A²+B²≠0）垂直的直线方程是B（x-x0）-A（y-y0）=0

3. 求过一点到已知直线夹角为定值的直线方程

定理3 过点M（x0，y0）且与直线Ax+By+C=0（其中A²+B²≠0）夹角为θ（θ≠Π/2）的直线方程是（Btanθ-A）（x-x0）-（Atanθ+B）（y-y0）=0

参考文献

1. 求与已知直线夹角为定值的直线方程的定理  张鑫  （甘肃省甘南师范学校 747000）