如果让您计算一个常规孔的位置度，相信不会太难，很多有经验的小伙伴马上就会想到那个经典的公式，见下图：

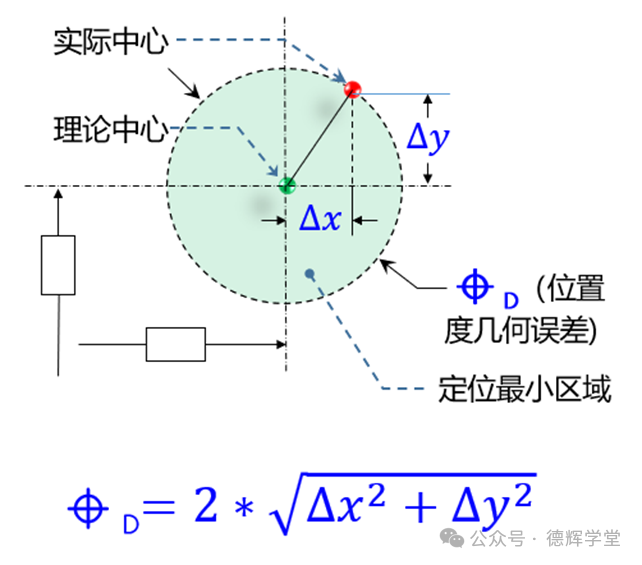
图1 位置度计算的经典公式

     图1中的公式，非常常见，也容易理解（假设您对常规的位置度计算原理还不清楚，建议您仔细看看上图，并仔细琢磨哦）。

     可是，如果有一天，我们遇到的被测孔的轴线，它的方向和坐标系的坐标轴既不平行，也不垂直，呈现某个夹角（也就是我们所说的斜孔），那么该斜孔的位置度该如何评价呢？

     比如，下面这个图纸：

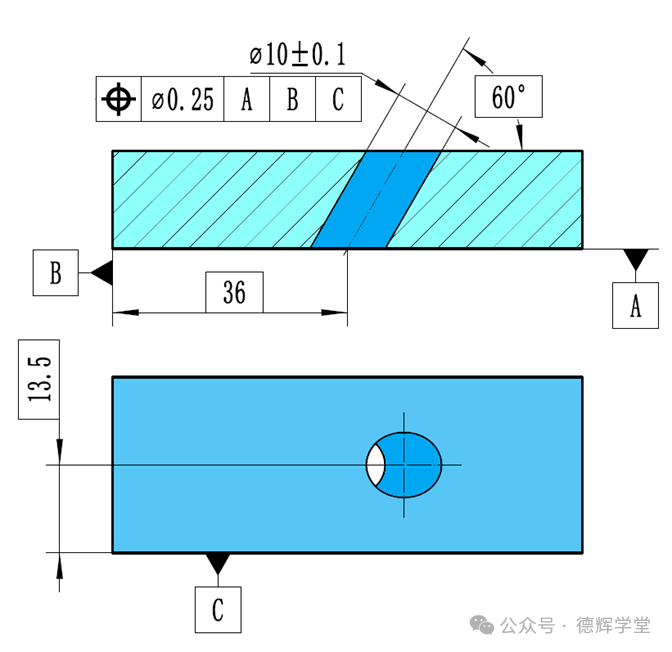
图2 斜孔的位置度

    图2的标注，就是对一个斜孔进行位置度控制。当零件被加工好后，三坐标工程师对实际零件进行测量，测量的结果如下：

    在基准坐标系xyz中，见图3，该被测孔的理论质心点P=(40.33, 13.5, 7.5)，理论单位矢量为n0=(0.5，0，0.866）， 已知实际提取中心要素（假设是ISO标准）上的最远点为P1点，而且已知该点在基准坐标系中的坐标为P1=(43.43,13.56,12.7)，求该斜孔的位置度实测值是多少？

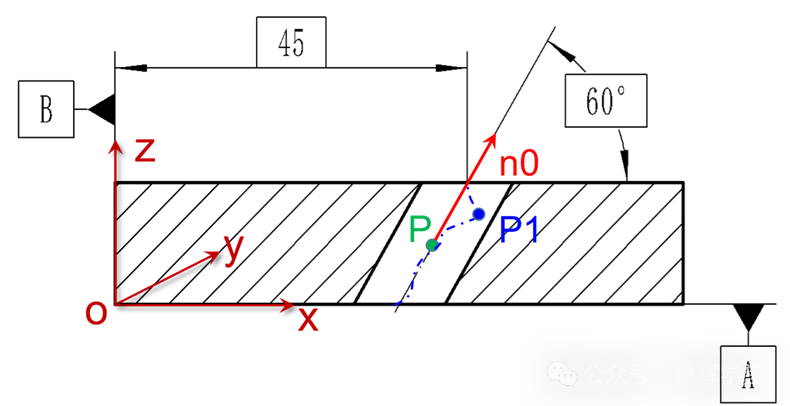
图3 求斜孔的实际位置度？

     上面的题目，实际上是我们进化群里出的一期题目，很多有经验的测量工程师都卡在这里，不知道该如何处理。

     要计算斜孔的位置度，它的评价原理比较简单，因为位置度的评价原理，都是“定位最小区域法”。本期题目的难点在于，后边计算的数学方法。

     所以，本期文章的内容其实就是在普及几个基本的数学知识点，它有助于我们理解几何误差计算的数学原理（数学好的小伙伴可以略过本文）。

     还是老套路，本期的题目我们分为3个章节来讲解：

    1. 什么是矢量？

    2. 单位矢量有什么好处？

    3. 斜孔的位置度如何计算？

    本期的内容数学味道会比较重，但是都很基础，如果您感兴趣，建议您耐心看完。

 1. 什么是矢量？

    矢量这个概念我们初中就学过，一个有大小，有方向的量就是矢量。比如我们学过的力，速度，加速度，位移等都属于矢量。见下图：

图4 常见的矢量

     我们课本上对矢量有个特点没有描述，那就是矢量本身隐含两个点，一个点是S点（Start Point）, 一个点是F点（Finish Point）, 而矢量的方向是从S点指向F点的。

动画1 矢量是相对量

     从几何上讲，矢量不仅有大小（即长度，或者叫模），也有方向，这个方向是一个相对的关系，是终止点相对于起始点的一个量。

     这个概念，我们在做公差分析的时候，也会用到，希望后边有机会和大家来探讨这个话题。

     矢量还有很多重要的性质，我们现在来一一认识一下  。 

1) 矢量坐标

      我们平时学过点坐标，比如某个点P1的坐标是（x1, y1, z1）, 在坐标系中的含义见下图：

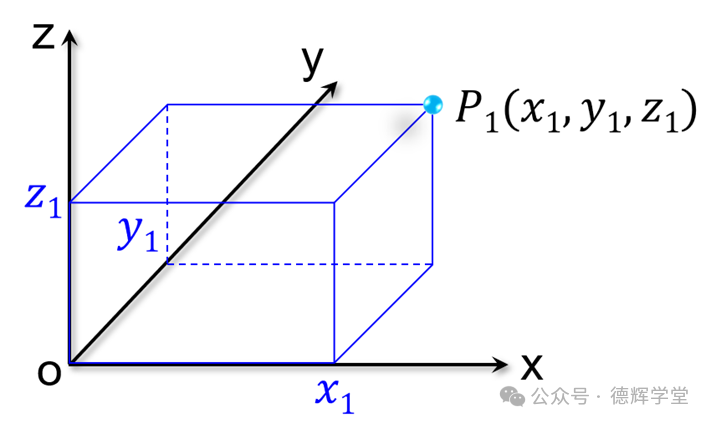
图5 P1的点坐标

     点坐标表达的是P1点在坐标系中的位置，或者说P1点分别在xyz坐标轴上的投影。

     注意，不同位置的点，它的坐标值是不同的。

     矢量也可以用坐标来表达，我们叫矢量坐标。我们刚刚讲过，矢量是指终止点F相对于起始点S的一个量，而所谓的矢量坐标，指的是将矢量的起始点S移到坐标系的原点O，然后终止点F在坐标系中的坐标，就是该矢量的坐标, 见动画2.

动画2 矢量坐标

     注意，在坐标系中，因为矢量是个相对量，大多数时候人们不关心它的位置，只关心方向（朝向），所以，矢量在坐标系中可以任意平移（不能旋转）。

2) 矢量的表达

     矢量应该怎么表达呢？矢量可以用坐标系的方式来表达，比如动画2中的矢量，我们可以表达成n1=（x1, y1,z1）.

     我们还可用坐标分解式（代数式）来表达。我们知道，在坐标系xyz中，每个坐标轴都有自己的单位矢量，我们叫i,j,k, 见下图（不了解这个概念的小伙伴，在公众号德辉学堂里搜相关文章，或者点击本文后的链接可以查看）。

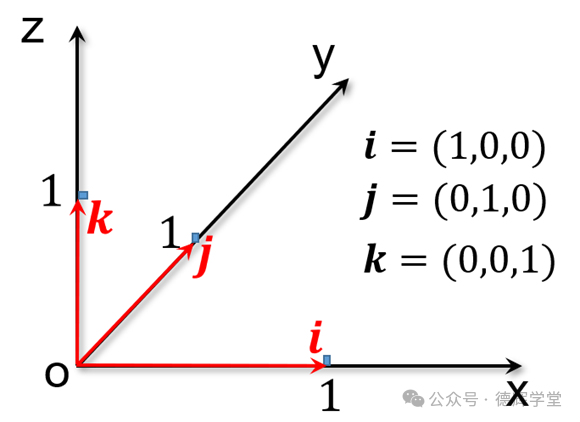
图6 坐标轴的单位矢量

     图6中，如果大家仔细观察三个坐标轴的单位矢量i,j,k，我们会发现，这3个单位矢量有个特点，那就是他们3个线性无关，也就是说这3个单位矢量，其中两个矢量无论如何线性组合，相加，相减，或者乘以一个常数，都无法表达成第3个矢量，上学那会儿叫线性无关。

     线性无关的矢量有什么好处？好处是他们可以张量成一个空间。我们说人话，就是三维空间中的任何一个矢量，我们都可用i,j,k的线性组合来表示。

     比如说，我们前面提到的矢量n1=（x1, y1, z1）， 可以表达成：

n1 = x1i+y1j+z1k

     上面的公式中，本质上就是3个矢量相加。注意，当我们把一个矢量乘以一个常数时，相当于把这个矢量的长度放大或者缩小了常数倍，矢量的方向不变。

     从几何上解释，如下动画所示(这里，矢量的相加，我们用了平行四边形法则)。

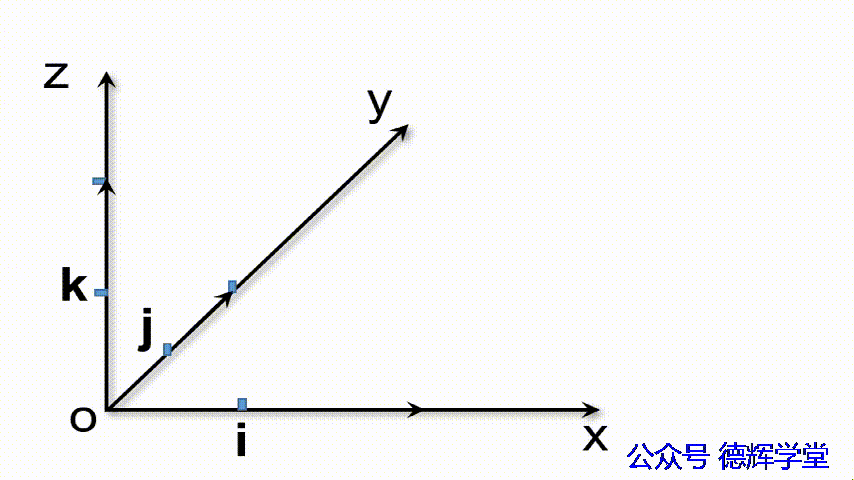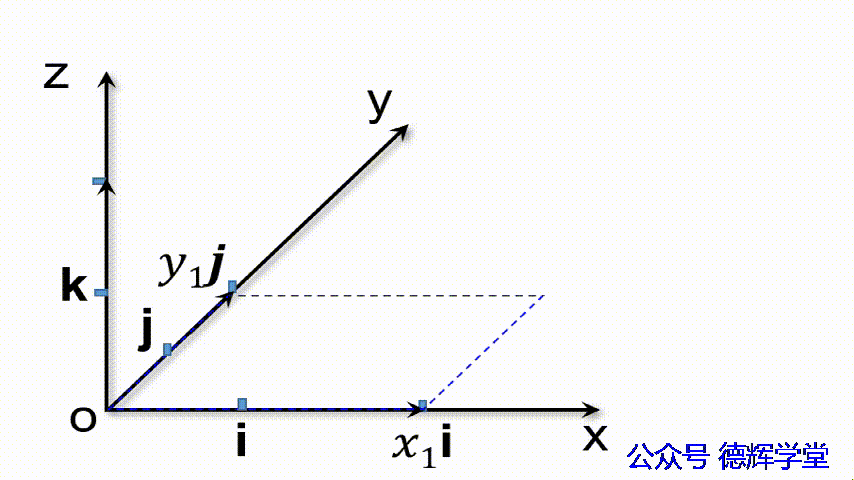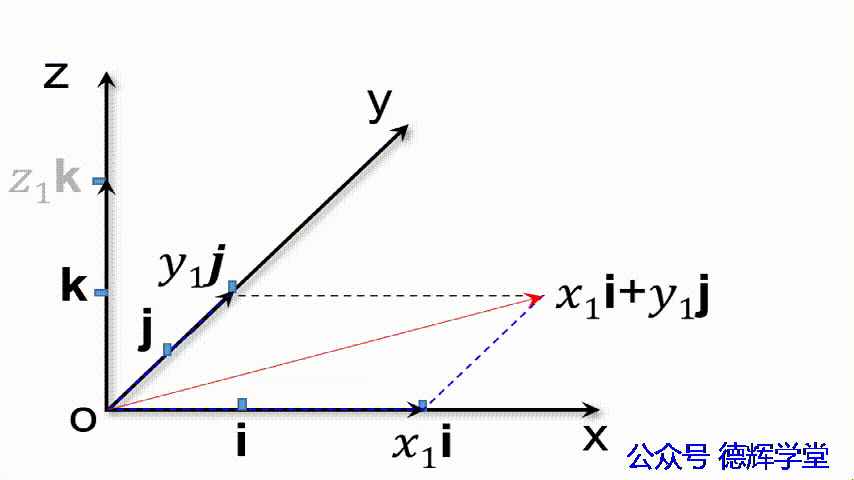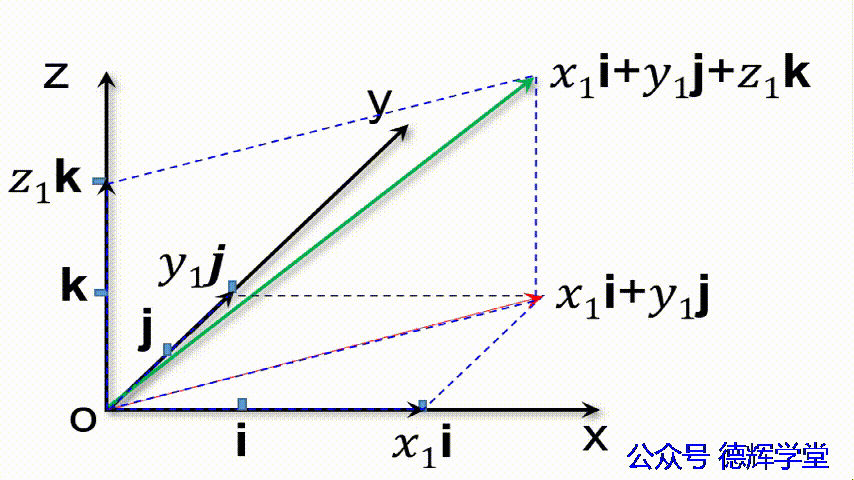
动画3 矢量的坐标分解式

     对矢量的表达，我们可以这样理解：

n1 = x1i+y1j+z1k= (x1, y1, z1)

     矢量表达成坐标分解式有什么好处？它最大的好处可以进行相关的运算，像代数一样，比如加法，减法和点乘，后边我们再来讨论这个话题。

3) 矢量的模（长度）

    矢量的模表示矢量的长度。我们仔细观察一下下面关于矢量的图形：

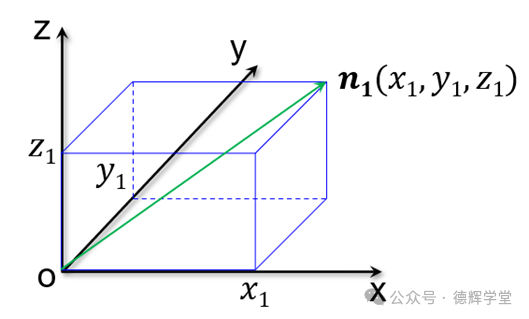
图7 n1矢量在坐标系中

     不难看出，图7中绿色的n1(x1, y1,z1)矢量的长度，实际上就是一个长方体的斜对角线的长度，而这个长方体的长宽高，正好是x1, y1, z1。

     所以，矢量n1的长度为：

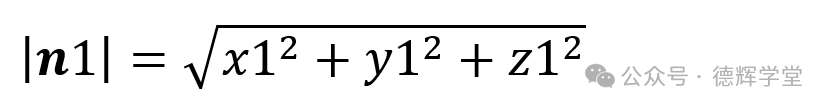
4) 矢量的加减法

     如果我们利用坐标分解式，矢量的加减法就会很容易。假设：

n1=x1i+y1j+z1k,n2=x2i+y2j+z2k,

     如果n3=n1+n2, 那么n3的结果为:

     n3=n1+n2

        = (x1i+y1j+z1k)+(x2i+y2j+z2k)

        =(x1+x2)i+(y1+y2)j+(z1+z2)k

     举个例子吧:

     假设a=2i+3j+4k, b=5i+6j+7k, 如果c=a+b, 求c？

    解：c=a+b

        =(2+5)i+(3+6)j+(4+7)k

        =7i+9j+11k

     注意，理解矢量加法的算法后，还需要理解矢量加法的几何含义，见下图：

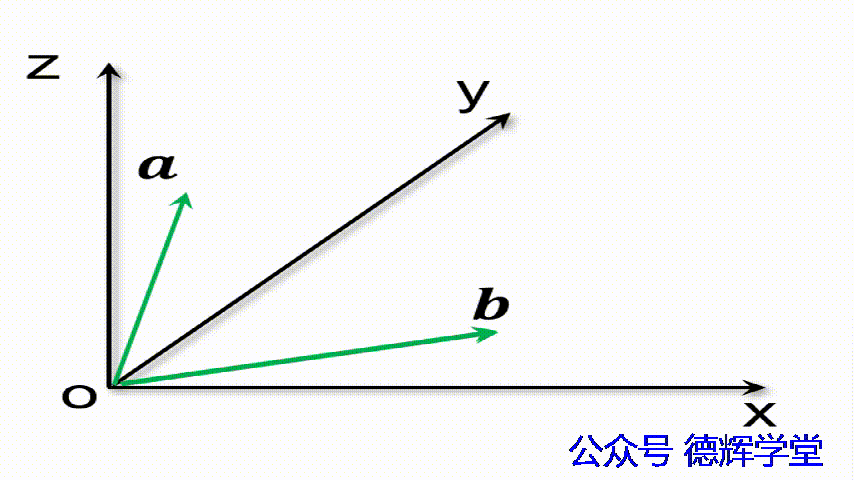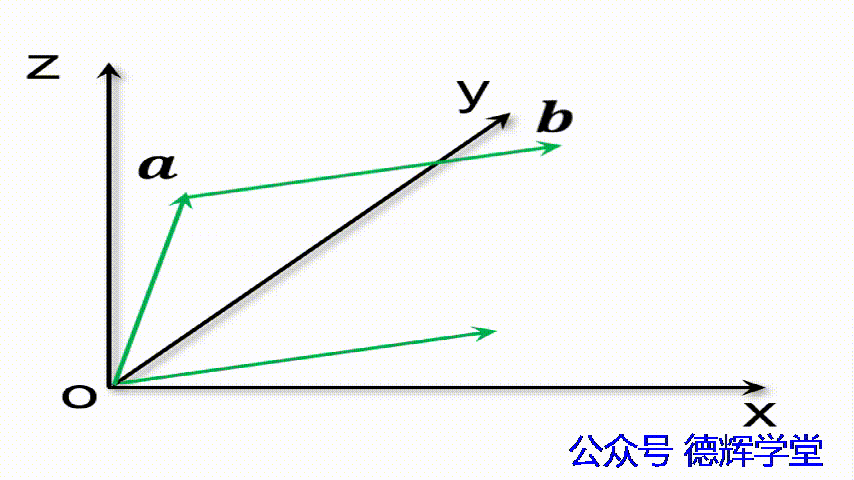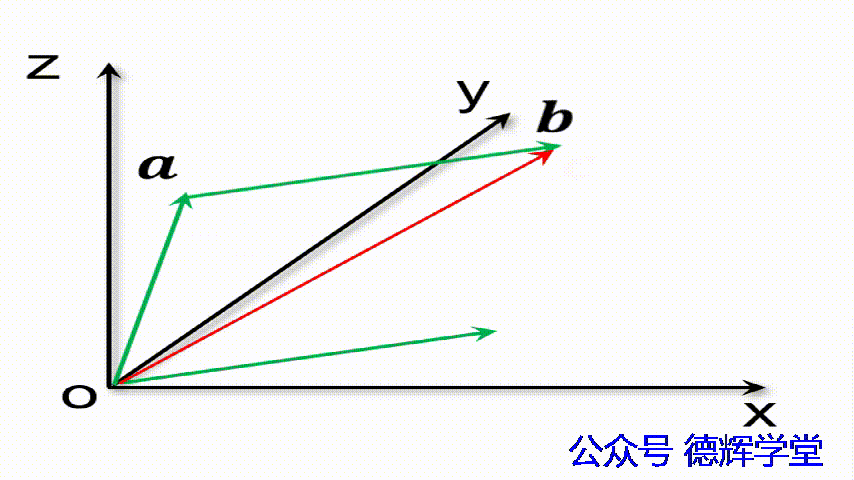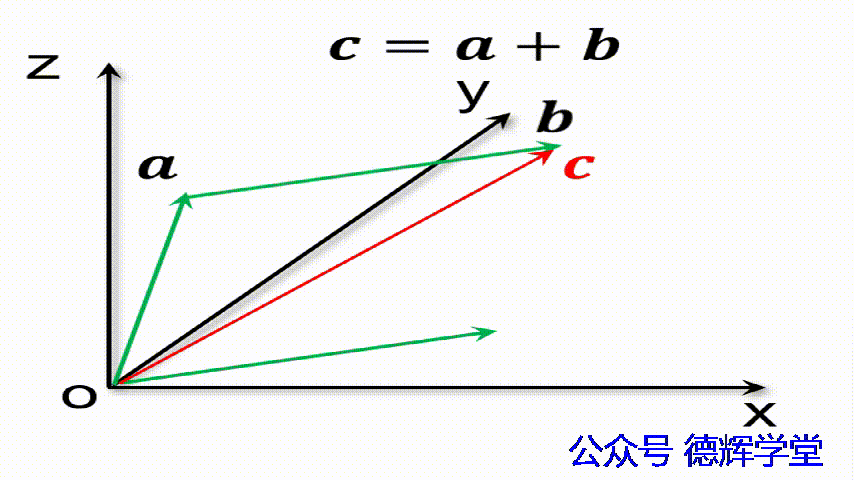
动画4 矢量加法的几何含义

     仔细观察上面的动画，我们会发现，矢量加数之间总是首位相连的。我们在用矢量法计算尺寸链的时候，也会用到这个特点（红色的就相当于封闭环）。

     废话少说，我们再来理解矢量减法的计算公式，假设：

n1=x1i+y1j+z1k, n2=x2i+y2j+z2k,

     如果n3=n1-n2, 那么n3的结果为:

     n3=n1-n2

        = (x1i+y1j+z1k)-(x2i+y2j+z2k)

        =(x1-x2)i+(y1-y2)j+(z1-z2)k

     是不是So easy?

     还是来举个例子，假设有两个矢量：a(2, 3, 4), b(5,6,7), 求a-b?

     根据上面提到的公式，显然有：

a-b=(2-5, 3-6, 4-7)=(-3, -3,-3)

     我们还是来看一下矢量减法的几何意义：

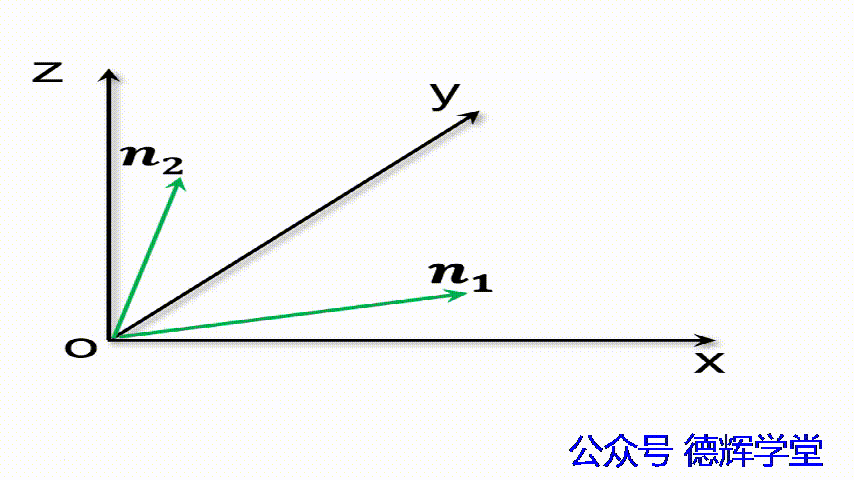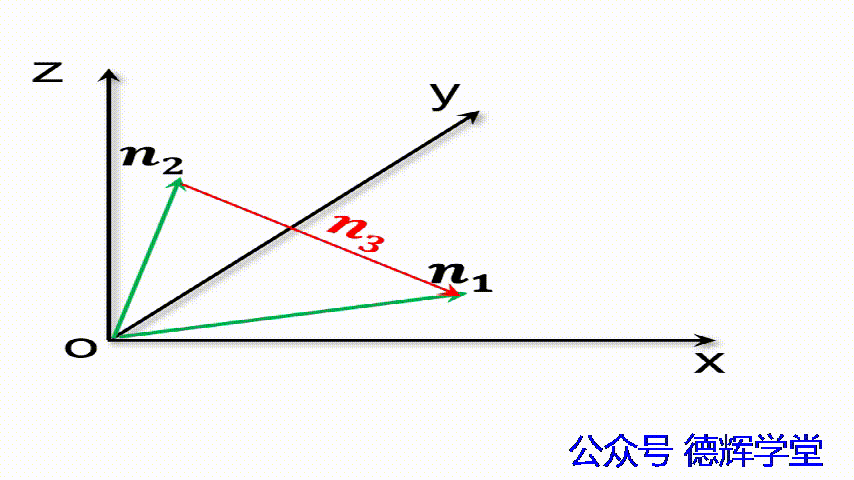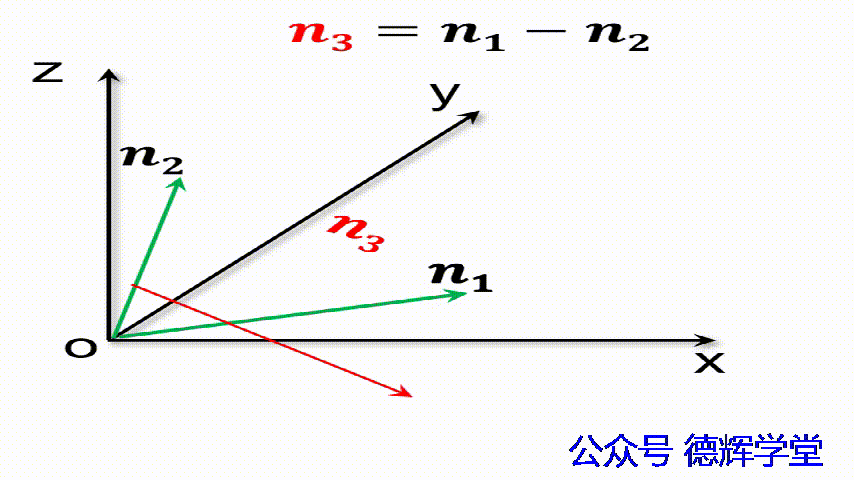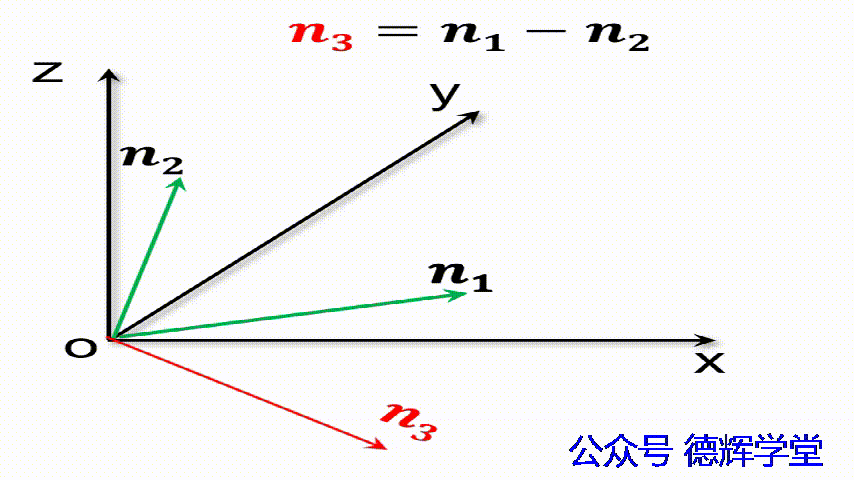
动画5 矢量减法的几何含义

     要稍微提醒的是，矢量的减法，它是从减数指向被减数。仔细观察上面的动画，n2和n3首尾相连，显然有n1=n2+n3,然后可以得出n3=n1-n2。这一点大家不要弄错，如果弄错了，我们会得到一个反方向的矢量。

5) 矢量的点积（数量积或者内积）

     矢量不仅有加减法，还有乘法。乘法又有两种，一个是点积，一个叫叉积，本期文章重点讲点积。

     先来看一个初中的物理题目：已知一个物体M在力F的作用下，位移为S,求该力作的功？

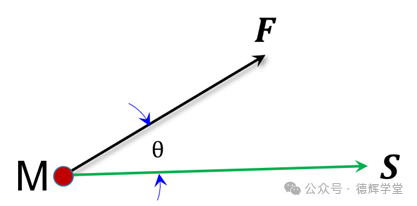
图8 力在某个位移方向上做功

     图8中，力和位移有一个夹角θ，根据初中的知识点，功的计算公式如下所示：

W=|F|*|S|*cos(θ)

     上面的公式中，显然表达的是力F在S方向上的投影（乘以一个余弦cos(θ)）和S的乘积，见下图。

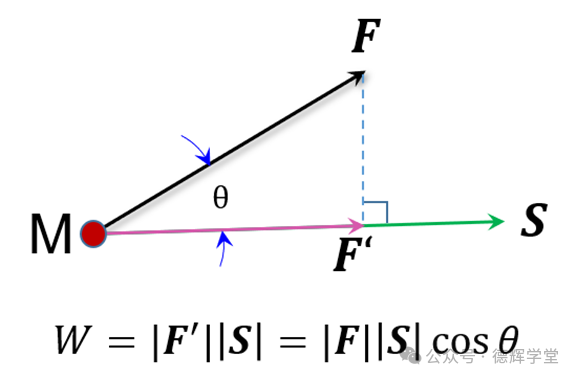
图9 功的计算公式

     图9中的公式，相信各位小伙伴都不陌生。其实，功的计算我们还可以直接采用矢量点乘的方式来表达：

W=F · S = |F|*|S|*cos(θ)

     从上面的公式中，我们可以看出来，两个矢量的点乘(中间有个点，叫点乘， 中间有个X， 叫叉乘)，它的结果是一个标量（功没有方向），它的大小等于每个矢量的模长相乘，再乘以两矢量之间夹角的余弦。下面是一般式：

n1 · n2 = |n1|*|n2|*cos(θ)        （1）

     注意，公式（1）是两个矢量点乘的公式，非常重要，它得到的结果是一个没有方向的标量（不是矢量），大家要记住。

     我们仔细观察公式（1）, 思考一下它的几何意义后，还可以得出一个结论，所谓矢量的点乘，它是将一个矢量投影到另外一个矢量上后，该投影的长度，再乘以后者的长度。这样说有点拗口，见下图：

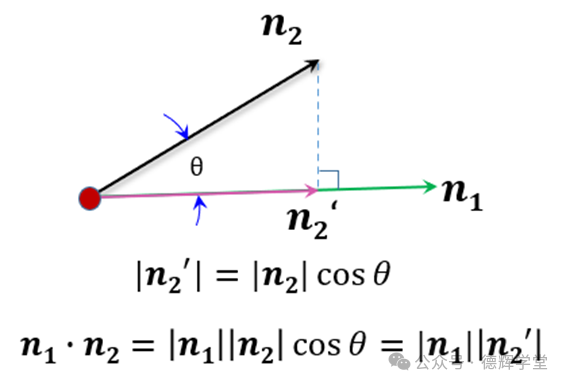
图10 将n2投影上n1上

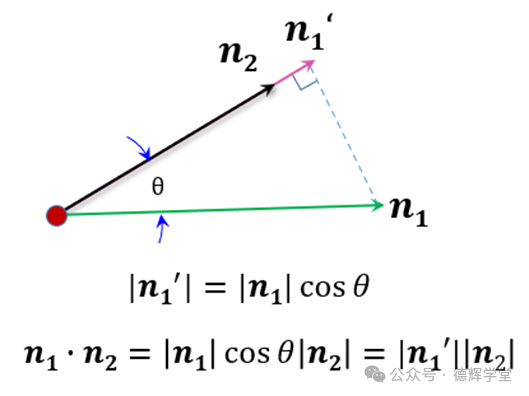
图11 将n1投影上n2上

     练习 前面讲过，单位矢量i=(1,0,0), j=(0,1,0), k=(0,0,1)请问，i · j=?  i · i = ?, i · k=?

     解：因为单位矢量i,j,k的模长为1，i和j的夹角是90度（余弦为0），i和i的夹角是0度（余弦为1）, i和k的夹角是90度（余弦为0）, 代入公式（1）所以我们可以轻松得出:

i · j = 0

i · i = 1

i · k = 0

     我们还可以进一步得出一个结论，针对三个坐标轴的单位矢量ijk, 如果我们任意排列组合抽出两个，进行点乘，可以得出一个结论：

     单位矢量相同，结果为1：

i · i = 1

j · j = 1

k · k = 1

     如果单位矢量不同，结果为0(因为垂直，投影长度为0)：

i · j = 0

i · k = 0

j · k = 0

     我们把上边这个特点叫“同1异0”， 后边我们在推导的时候还要用到这个特点。

     在前面的公式（1）中，我们如果要计算两个矢量点乘的结果，还需要知道两个矢量的夹角θ，非常麻烦，不利于计算。

     如果我们使用矢量坐标或坐标分解式来表达矢量，计算两个矢量的点积就会很轻松。

    已知 n1=x1i+y1j+z1k, n2=x2i+y2j+z2k, 求n1·n2?

    显然有：

 n1·n2 = (x1i+y1j+z1k)·( x2i+y2j+z2k)

     上面的公式看起来很庞大，苦逼，无奈的样子，如果我们耐心把上边的括号打开，一个一个乘进去，再利用“同1异0”的特点，我们可以得出一个惊天大瓜：

n1·n2 = x1*x2+y1*y2+z1*z2           （2）

     就这？

     是的，就这。非常简洁。

    趁热打铁，我们赶紧利用公式（2）做个练习：

    练习 已知n1=(1,2,3), n2=(4,5,6), 求n1·n2?

     解：根据公式（2）

n1·n2=1*4+2*5+3*6=32

    如果利用Excel计算，可以用函数sumproduct（）来实现。比如：

n1·n2=Sumproduct(n1,n2)

     有兴趣的小伙伴，赶紧用Excel玩一下。

     公式（2）也非常重要，我们通常利用公式（1）和公式（2）来求两个矢量之间的夹角：

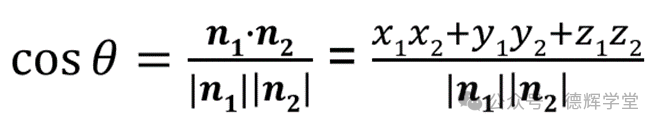
     这个和我们今天的主题没有关系，有兴趣的小伙伴可以单独深入研究。我们继续往下走。

2. 单位矢量有什么好处？

     除了测量软件，在其它软件上，比如公差分析软件，3D造型软件，我们也经常看到单位矢量这个概念，它有什么好处呢？我们现在就来认识一下单位矢量。

     在第一章节，我们就学过单位矢量，比如ijk就是沿着三个坐标轴xyz方向的特殊的单位矢量，它的最大特点就是该矢量的模长为1.

     我们来看一下一般的单位矢量，见下图：

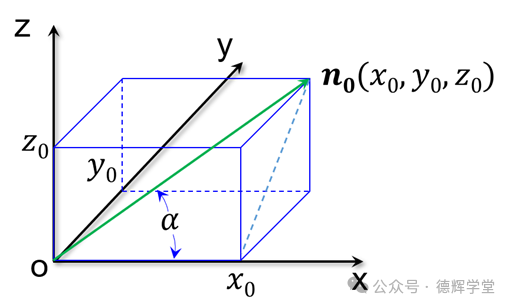
图12 单位矢量n0

     图12中，如果n0是一个单位矢量，根据单位矢量长度为1的特点，则有下面的关系：

     如果我们希望求出该单位矢量和x轴的夹角余弦cos(a), 从图12中不难看出：

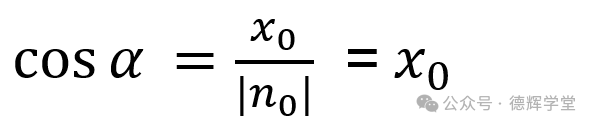
     同理，我们不难得出，该矢量和xyz轴的各自的夹角余弦：

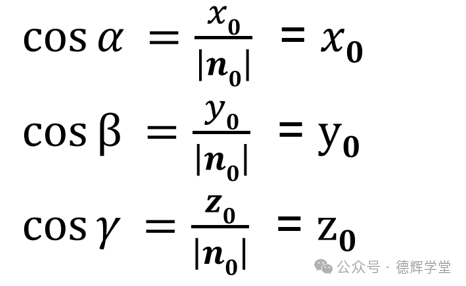
    所以有些资料介绍，单位矢量n0可以表示为（cos(α), cos(β), cos(γ)），其实也就是（x0, y0, z0）了。

     单位矢量有什么好处呢？

     结论 任何一个矢量和单位矢量的点乘，其结果等于该矢量在单位矢量上投影的长度。

     这，就是单位矢量最大的好处之一，可以用来算投影的长度。

    上面这句话如果没有吃透的小伙伴，建议再看一遍。

     我们快速证明上述结论，我们再调出公式(1)：

n1 · n2 = |n1|*|n2|*cos(θ)    （1）

     将公式(1)中的n1换成单位矢量n0, 我们得到以下结果：

n0 · n2 = |n0|*|n2|*cos(θ)

    又因为n0是单位矢量，长度为1，即|n0|=1，所以有：

n0 · n2 = |n0|*|n2|*cos(θ)= |n2|*cos(θ)=T  （3）

     上面公式的几何意义，见下图：

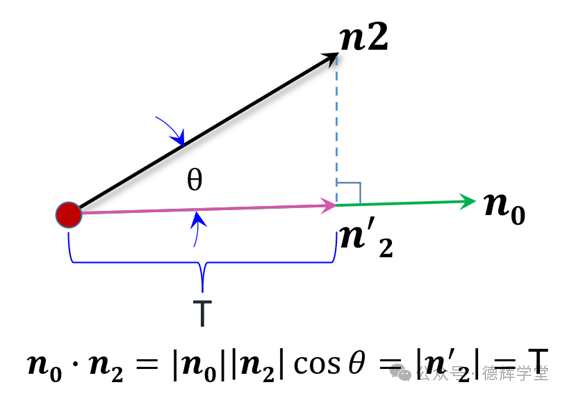
图13 单位矢量和投影T

     也就是说， 如果我们知道一个矢量n和单位矢量n0,我们就可以轻松算出矢量n在单位矢量n0上的投影长度T。

    我们再进一步把结论整理成一个“投影定理”：

    已知矢量n1的矢量坐标为（x1, y1, z1）,单位矢量n0的坐标为（x0, y0, z0）, 则n1在n0上的投影长度T为：

T=n1·n0 = x1*x0+y1*y0+z1*z0    (4)

     注意公式（4）也非常重要，我们在计算位置度时要用到。

    例：请计算矢量n1(5,7,9)在单位矢量k(0,0,1)上的投影长度T。

根据公式（4），T=n1 · k

                   =5*0+7*0+9*1

                    =9

     上面的计算确实无聊，根据矢量的定义，n1(5,7,9)在z轴（单位矢量是k）上的投影长度当然是9，但这也间接的证明了这个公式的正确性。

     好了，到这里，该铺垫的已经铺垫了，我们继续往下走。

3. 斜孔的位置度如何计算？

     有了充分的理论铺垫后，我们现在就可以计算斜孔的位置度了。我再把本文开头的题目放在这里：

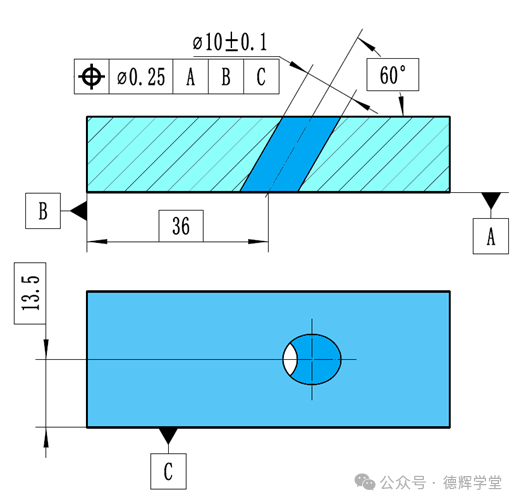
图14 图纸标注

     三坐标测量的信息如下图所示：

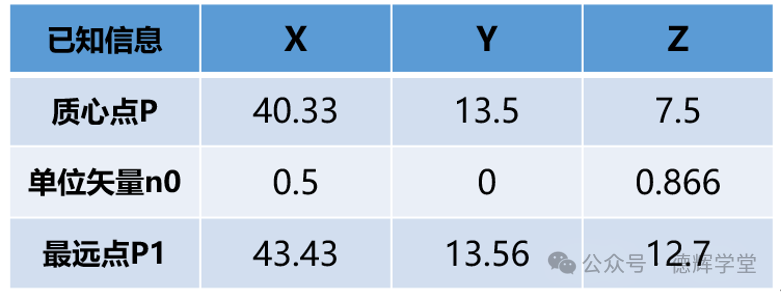
图15 三坐标测量原始数据

     在开始计算之前，我们稍微扯一下位置度的评价原理。再说一遍，所有位置度的评价原理都是定位最小区域法，斜孔的位置度也不例外。见下面动画：

动画6 定位最小区域法

     见动画6中显示，定位最小区域的直径D，就是位置度的实际测量值，只要我们能够计算出D值，结果就出来了。

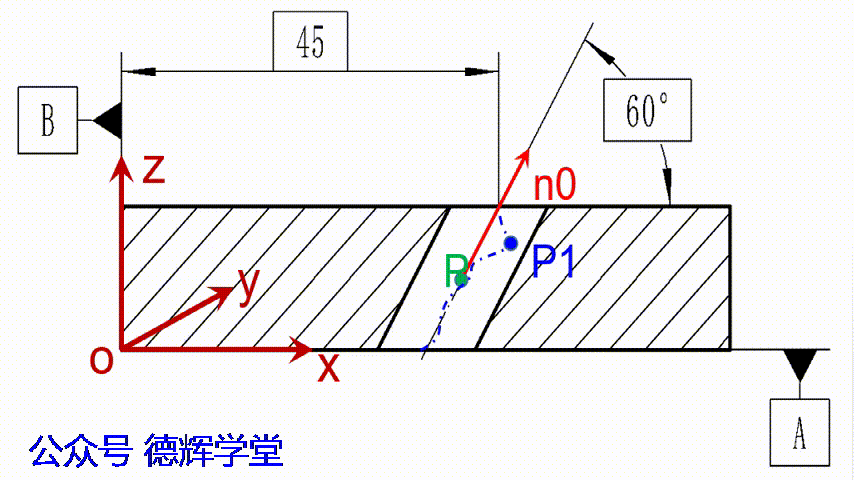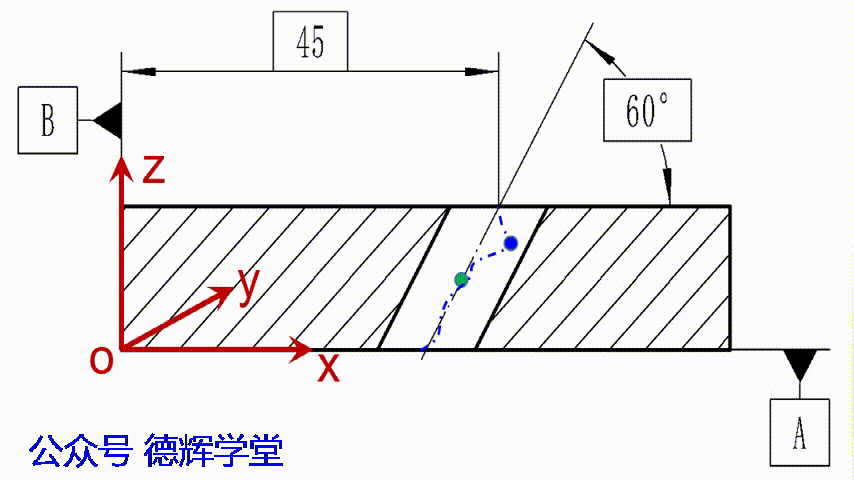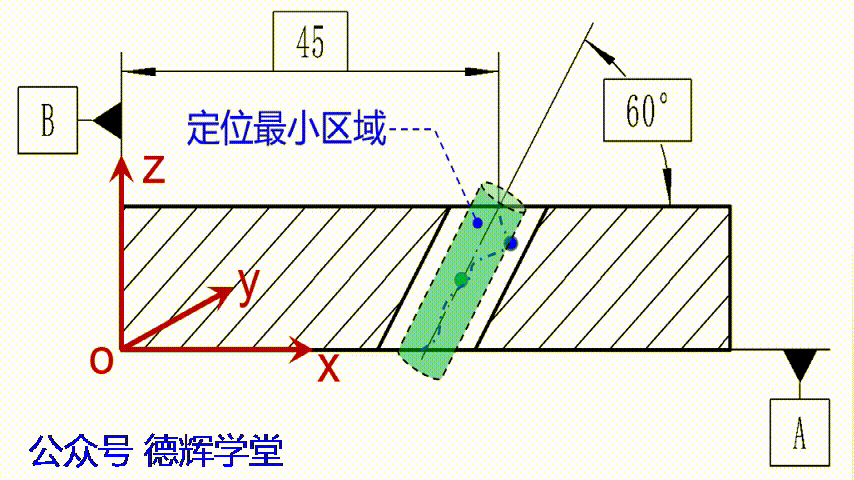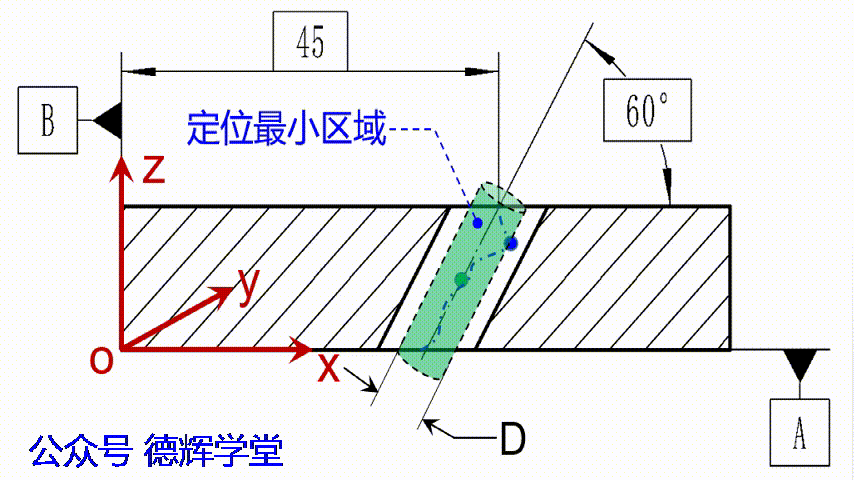
     我们再把图15中的问题提炼成为几何问题，见下图：

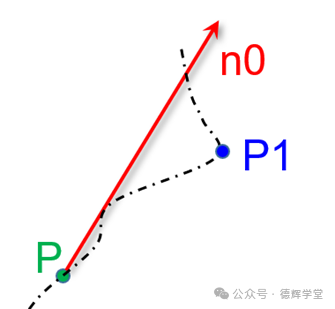
图16 提炼后的几何问题

     图16中，我们将单位矢量n0的起始点S固定在质心点P上，然后，只要能求出最远点P1到n0的距离，再乘以2，就可以得到实测位置度D值。

     我们现在相当于在作一个几何题，做好一系列的辅助线后，图示如下：

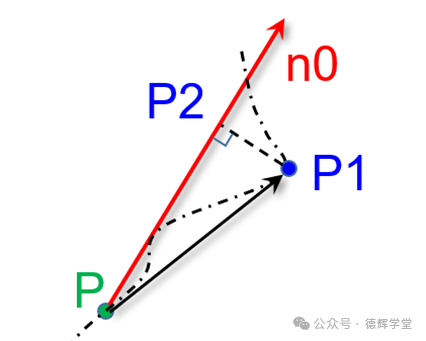
图17 计算位置度D

     见图17，我们先连接PP1, 构造一个矢量PP1, 然后把最远点P1点向单位矢量n0作投影，得到垂足P2。显然，P1P2距离的2倍就是位置度的实际测量值。即：D=2*|P1P2|.

    现在的问题是，如何求P1P2的长度？

    图17中，🔺PP1P2是一个直角三角形，|PP1|这个斜边的长度容易算出来，如果我们能计算出PP2的长度，再利用勾股定理，就可以计算出|P1P2|了。

     我们先把原始数据放在这里：

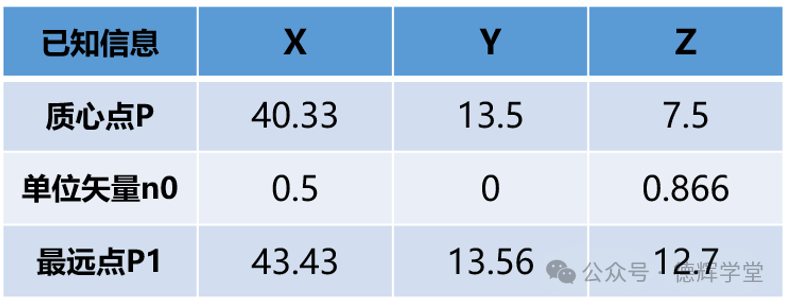
图18 原始数据

     先构建矢量PP1（注意，原点O指向该点形成矢量，其矢量坐标，就等于该点的点坐标）。

     PP1=OP1-OP（O表示坐标原点）

     =（43.43,13.56,12.7)-(40.33,13.5,7.5)

     =(3.1,0.06,5.2)

     根据上面的坐标，利用立方体的斜对角线，平方和开根号那个公式，我们很容易算出:

     |PP1|=6.054。

     再根据“投影定理”，我们可以计算出：

     |PP2|= PP1·n0

    = (3.1,0.06,5.2)·(0.5,0,0.866)

   =3.1*0.5+0.06*0+5.2*0.866

   =6.053

     再根据勾股定理可以得出：     

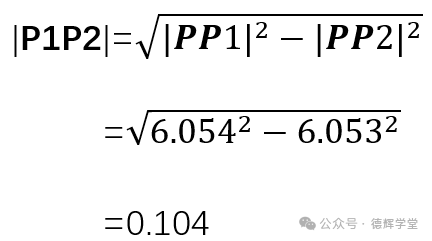
    D=2*|P1P2|=0.208

     欧了。

     事实上，我自己把计算过程做成一张Excel表格（有兴趣的小伙伴可以加我微信索要），计算的原始数据如下：

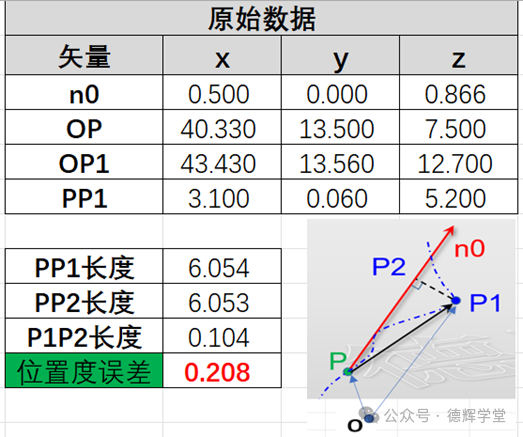
图19 计算原始数据

     内容到这里就完了，希望本期对您有所启发。

【内容总结】

     本期内容我们主要讲了斜孔位置度计算的数学原理。

     首先我们讲了矢量的特点，矢量坐标，矢量的模，加减法，点乘，然后又讲了单位矢量的好处，比如那个投影定理，这些都是我们上学那会儿学过比较基础的知识。最后再利用最小定位最小区域法，计算斜孔的位置度。

     本质上讲，本期内容就讲了一个数学知识点，如何计算空间中的一个点到一个空间直线的距离。

     本期的内容主要还是数学关于矢量的一些知识点。其实, 为了算最远点P1到单位矢量n0的距离|P2P1|, 我们还有更加简洁的方法，那就是利用单位矢量的叉乘，比如: |P2P1|=|PP1xn0|, 直接得出结果，但是矢量的叉乘计算不太容易，要用到行列式或者反对称矩阵转化处理，解释起来更加痛苦。