在ISO标准或者国标的工程图纸中，我们可能会看到下面的标注：

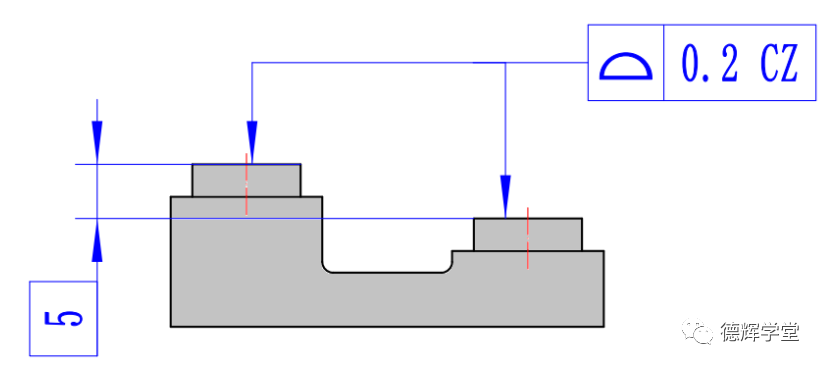
图纸：带CZ的标注

图中的轮廓度仅仅控制表面的形状吗？如果是，那么供应商是不是把每个表面加工的足够平整就一定能满足图纸要求？

图中的修饰符号CZ表示什么意思，公差带具备什么样的特点？设计者究竟想要什么？

要彻底理解这些问题的本质核心，我们必须要理解什么是内约束，什么是外约束。

对很多工程师来说，内约束，外约束，这可能是个新名词，但是，它是一条非常重要的概念或者思路，涉及整个基准体系系，除形状公差外的所有几何公差，以及成组要素的终极目标。

内外约束，有点类似我们人体中的中枢神经，是GPS或GD&T的核心。

本期文章我们就来初步探讨一下内约束和外约束。本篇文章将分为4个部分来分别来讨论。

1. 鸟笼模型与约束的分类

2. 3种内约束

3. 外约束与内约束的相互关系

4. 内外约束的应用案例

本期文章，我们先放送前面两节。

1. 鸟笼模型与约束的分类

我以前在给学员上课的时候，一再强调图纸的逻辑，设计者在图纸上标注几何公差，表达的就是公差带，通过公差带去约束被测要素（被控制的特征）。

为了帮助大家能够轻松理解内约束和外约束这个概念，我建立了一个“鸟笼模型”，理解了这个鸟笼模型，再来理解今天的话题就非常容易了。

     公差带和被测要素的关系，就是鸟儿和鸟笼的关系，见下图。对于所有的工程师来说，只要鸟儿老老实实呆在鸟笼里，大家皆大欢喜。

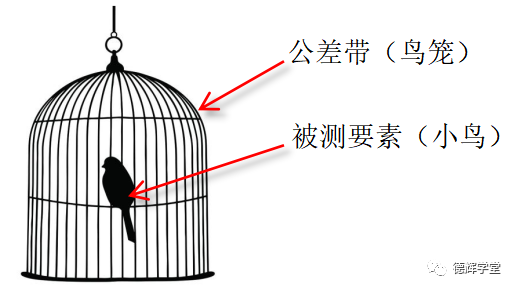
图1 公差带和被测要素

而鸟笼本身，也可能会被限制起来，比如鸟笼会被挂在阳台上的晾衣架上，那么晾衣杆对鸟笼就构成了约束，它限制了鸟笼的某些自由度，这个晾衣杆，在工程图中，就是我们常见的基准。

图2 公差带被约束

我们再往下走。

     现在，我家有两个鸟笼，我先用绿色的连接杆将两个鸟笼连接起来后，再将两个鸟笼挂在阳台上的晾衣杆上。见图3。

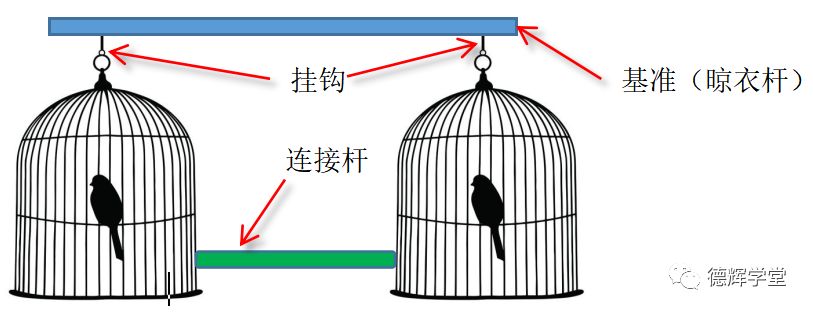
                  图3 两个鸟笼被固定

我们仔细观察图3中的两个鸟笼，我们会发现此时鸟笼受到到两个约束，一个约束是来自绿色的连接杆，一个约束是来自晾衣杆。

     好了，这就来到了我们今天的主题，绿色的连接杆是控制了鸟笼和鸟笼之间的相对关系，我们把它造成的约束叫内约束（Internal Constraint），而晾衣杆通过挂钩造成的约束叫外约束（External Constraint）。见图4。

图4 内约束和外约束

约束本来就是几何公差的核心内容，内约束和外约束这个概念是ISO标准提出来的, 不是个新鲜事。但是能够把公差带受到的约束分为内约束和外约束两类，这本身就是一个认知的进步。

扯了半天，那么具体到图纸上，怎样才能体现内约束和外约束呢？

不急，我们慢慢往下走。往下走之前，请各位小伙伴一定要记住图4中的鸟笼模型。

2. 3种内约束

接下来我们就专门探讨内约束。在ISO标准中，要体现内约束，必须要加相应的修饰符号。修饰符号一共有3个，分别是CZ, CZR, SIM, 一旦加了修饰符号，就意味着在公差带和公差带（鸟笼和鸟笼）之间增加了内约束（连接杆）。

图5 内约束的修饰符号

2.1 组合公差带CZ. 

说起ISO或者国标中的CZ，人们见过最多的就是用在平面度上，以前的术语名称是“公共公差带”（Common Zone）。根据最新的ISO5458：2018，最新的术语更改为“组合公差带”（Combined Zone），它的本意是把多个公差带（鸟笼）整合（Combine）在一起。

     如下图所示：

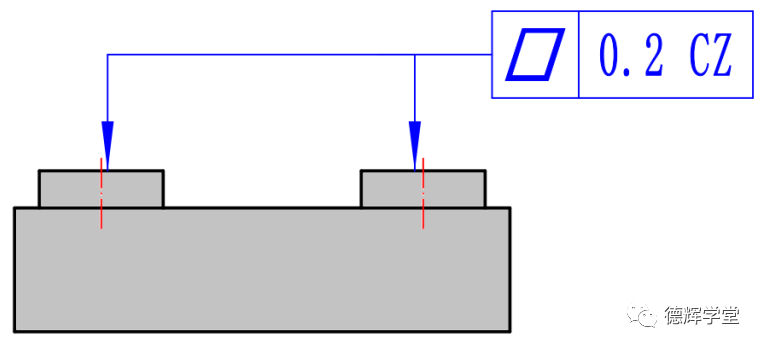
图6 平面度带CZ的标注

很多工程师对图6的理解是控制两个平面“共面”，理解成控制共面要求也没有错，但是，这样理解容易让人忽略CZ的本质。

我们先来看看平面度加CZ本来的含义：

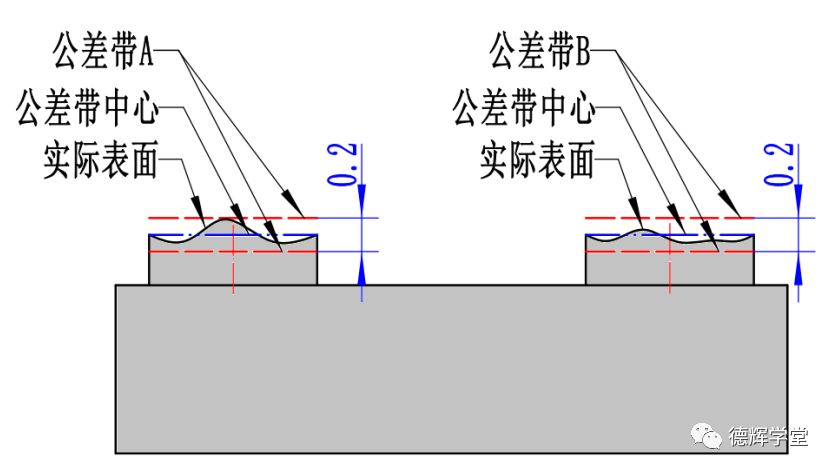
图7 平面度带CZ的含义

由平面度的概念可知，平面度的公差带是两个相距为0.2的两平行平面之间的区域，如图7中的公差带A和公差带B.

那么平面度加了修饰符号CZ后的含义是什么呢？

平面度加了CZ后， 如同在鸟笼之间增加了一个连接杆，它的目的固定鸟笼和鸟笼之间的相对关系， 所以CZ的目的就是固定公差带A和公差带B之间相对关系，即要求两公差带之间必须保持理想的方位关系！

啥意思？要求公差带A和公差带B相互之间必须绝对平行，相互距离是0（相对方位关系是固定的）。见图8。

因为公差带A和公差带B要相互平行，且距离是0，实际上就是“对齐”。

只要零件的实际表面能够同时落到AB两个“对齐”后的公差带里，该零件就是合格的。

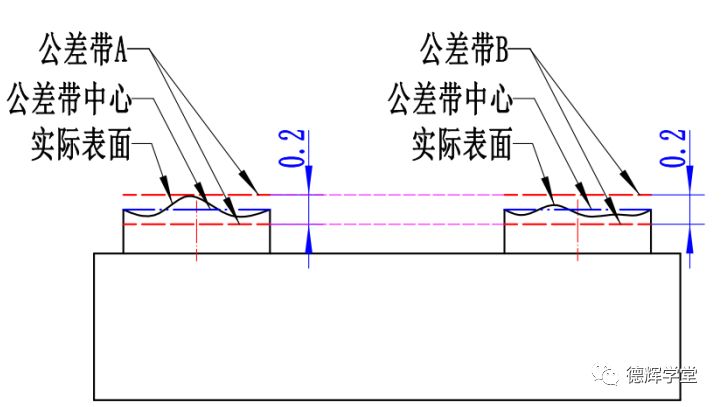
图8  “对齐”后的公差带

通过图8我们可以看出，设计者的意图是，希望左右两个平面能够在一个平面上（理想状态），也就是我们所说的“共面”。

那么是谁要求公差带相互之间必须要求对齐呢？显然，就是这个代表内约束的修饰符号“CZ”。

本来平面度作为形状公差，它的公差带的方向和位置是自由的，没有人管控的，但是加了CZ后，公差带的方向和位置就不能为所欲为了，他们相互之间必须步调一致，所以公差带是受到了内约束（注意，因为没有外约束，只要公差带能够对齐，作为整体，方位关系还是自由的，没人管控）。

再一次强调，内约束强调的是公差带和公差带之间的关系，也就是鸟笼模型中的那根绿色连接杆的功能，不是公差带和基准之间的关系（鸟笼和晾衣杆之间的挂钩功能）。

鸟笼模型中绿色的连接杆的功能是固定鸟笼和鸟笼之间的相对关系，那么显然使用绿色连接杆必然有个前提，那就是必须要有2个或2个以上的鸟笼，使用这个连接杆才有意义。

同样的逻辑，内约束强调的是公差带和公差带之间必须保持的一定关系，那么就必须要求存在2个或2个以上的公差带。也就是说，内约束针对的对象一定是特征组！

所以，当采用CZ的时候，针对的对象必须特征组，也就是我们说的成组要素。

如果CZ被用在单个特征上，那个设计工程师一定是菜鸟。

见下图：

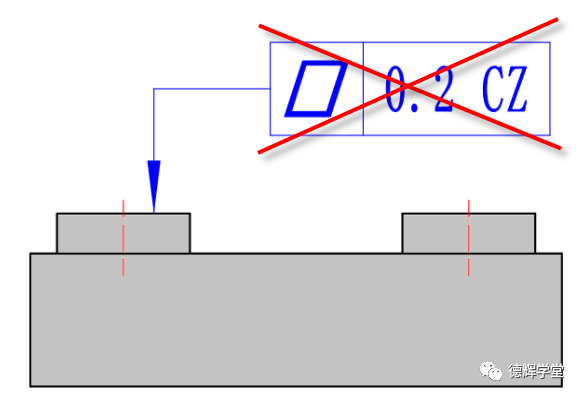
图9 单个特征不能用CZ

     还有一点，CZ作为鸟笼之间的连接杆，它必须应用在相同的鸟笼之间，不同的鸟笼是没有办法应用的（不同的特征控制，接下来会讲）。所以针对的对象除了是特征组以外，还必须是相同的特征，我们常常在图纸上见到的“2x”，“3x”就表示控制的是相同特征。见图10。

图10 CZ应用在相同的特征

我们再进一步，既然CZ是要求内约束，即要求公差带和公差带之间必须保持理想的关系，那是什么样的理想关系呢？

回答这个问题前，我们首先要回答的问题是，公差带和公差带之间有些什么样的关系可控制？

到这里，我们先插一个话题。我们知道公差带在空间坐标中有6个自由度，分别是x,y,z,u,v,w。其中， x,y,z是沿三个坐标轴方向的平移，u,v,w是绕三个坐标轴方向的旋转。

我们把x,y,z三个平移的自由度叫位置（Location），把u,v,w三个旋转的自由度叫方向（Orientation）。

我们平时指的“方位”关系，就是指的方向和位置关系。重复一遍，“方位”是两个维度上的要求，方向+位置。

在回到主题，CZ要求公差带和公差带之间必须保持理想的关系，这个理想的关系究竟指的是什么关系呢？

答案是：“方位”关系。即采用了CZ后，公差带和公差带相互之间，不仅仅要保持理想的方向关系，还要保持理想的位置关系。

     再来看一个案例，比如本篇文章一开始提到的那个标注：

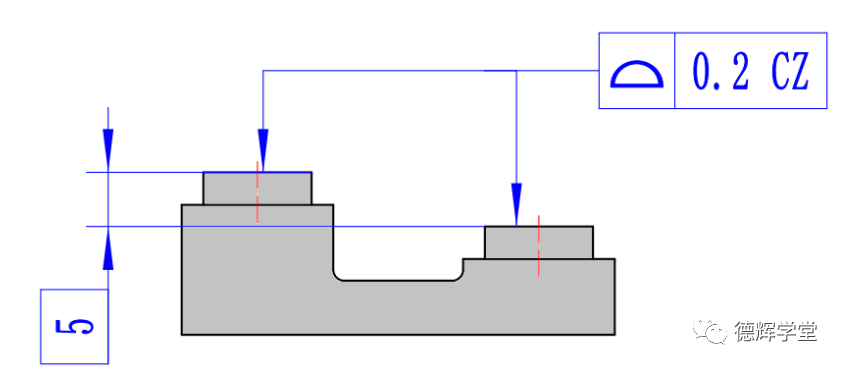
A. 图纸标注

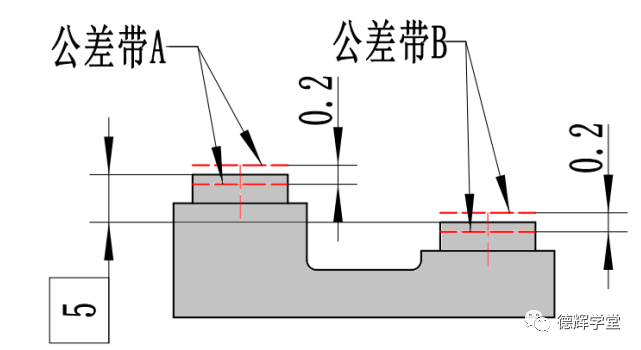
B. 公差带

图11 公差带之间保持方位关系

图11中的A图，因为采用了CZ，它就要求公差带和公差带之间必须保持理想的“方位”关系，即在B图中，公差带A和公差带B相互之间必须绝对平行（方向关系），其公差带A的中心到公差带B的中心的距离必须是绝对的5（位置关系）。

讲到到这里，可能有小伙伴开始不耐烦了，内约束要求公差带之间保持方位关系，这不是天经地义吗？难道还有其它可能吗？

还真有可能，因为在ISO标准里边，表达内约束，还有一个修饰符号，叫CZR, 仅约束方向的组合公差带，它的内约束的方式又不一样。

2.2 CZR 仅约束方向的组合公差带

     废话少说，直接上图：

图12 采用CZR的内约束

如果图纸中的内约束采用CZR, 它要求公差带和公差带之间只需要保持方向关系（平行），不需要保持位置关系。

也就是说，如果实际零件做成台阶状，按照图12的要求，也是合格的。见图13。

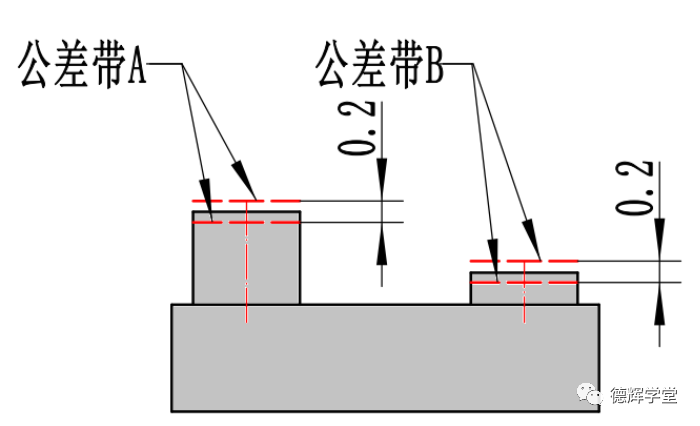
图13 采用CZR后合格的零件

见图12，只要采用了CZR，就要求图13中的公差带A和公差带B相互之间必须理想平行，而相互之间的距离则没有要求，这就是为什么对于图12的标注来说，图13中的零件也是合格的。

图13体现的是“相对平行度”。

同CZ一样，CZR针对的是相同的多个鸟笼，也就是说，只有对2个或2个以上的相同特征进行控制时，才能采用CZR.

问题又来了，如果我想控制不同特征相互之间的关系，那该怎么控制？

没问题，我们用SIM, 同时要求！

2.3 SIM 同时要求

除了CZ, CZR以外，表达内约束还有一个修饰符号，那就是SIM, 即同时要求（Simultaneous)。见图14。

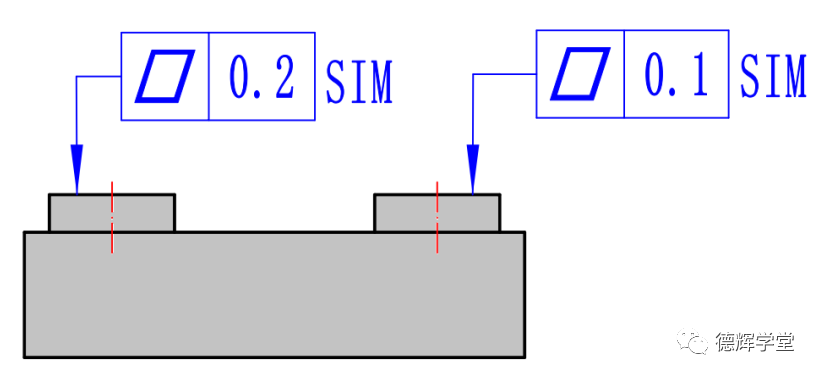
A. 采用SIM的标注的图纸

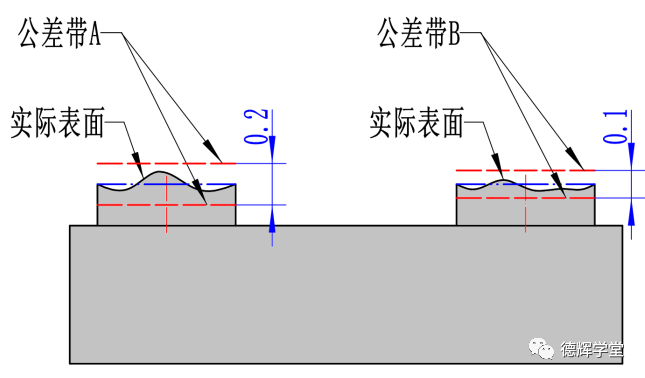
A. 采用SIM的标注后的公差带

图14 采用SIM标注

SIM应用在几何公差之间，要求各几何公差的公差带相互之间必须保持理想的方位关系。

图14中，0.1的平面度和0.2的平面度后边都采用了修饰符SIM， 就意味着要求公差带A（平面度0.2）和公差带B（平面度0.1）相互之间必须理想平行，且距离为0. 换句话说，要求两个公差带的中心要“对齐”。最后实际零件的实际表面必须同时落在两个“对齐”的公差带里边（尽管公差带的大小不一样），才算合格。

要强调的是，SIM和CZ类似，要求公差带和公差带相互之间必须保持理想的方位关系，是方向和位置，方向和位置哦。

     另外还要强调的是，SIM最大的特点在于， 它可以将不同形状的鸟笼连接起来。（这一点CZ和CZR是做不到的）。

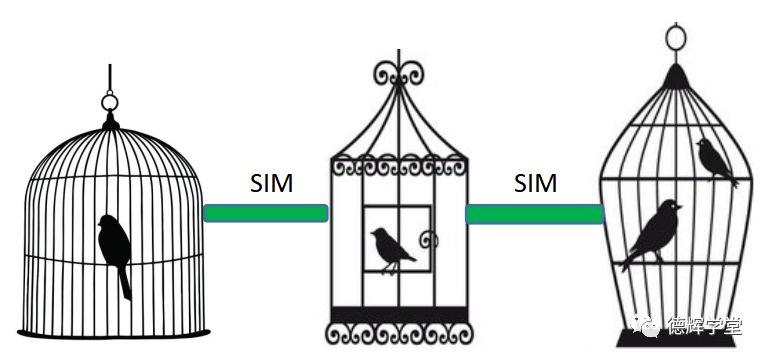
图15 SIM固定不同形状的鸟笼

     什么叫将不同形状的鸟笼连接起来？不扯犊子，上个图说明问题吧。见图16：

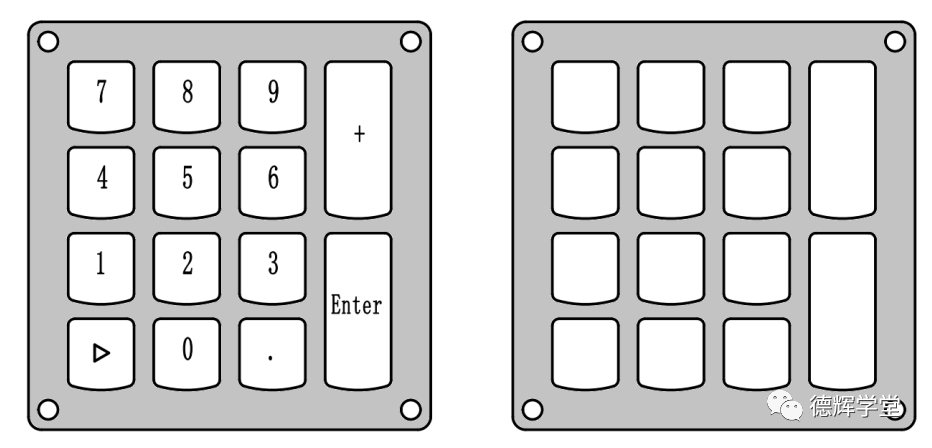
键盘                              键盘面板

图16 键盘和键盘面板

图16是键盘和键盘面板，在装配的时候，我们希望所有的按键孔，螺钉孔以及周边轮廓都能和PCBA上的元器件精确对应，使得装配时不发生干涉，如何控制键盘面板？

此时，对相同的特征除了采用CZ外，我们还可以采用SIM来约束不同特征之间的关系。键盘面板的具体标注如下图所示：

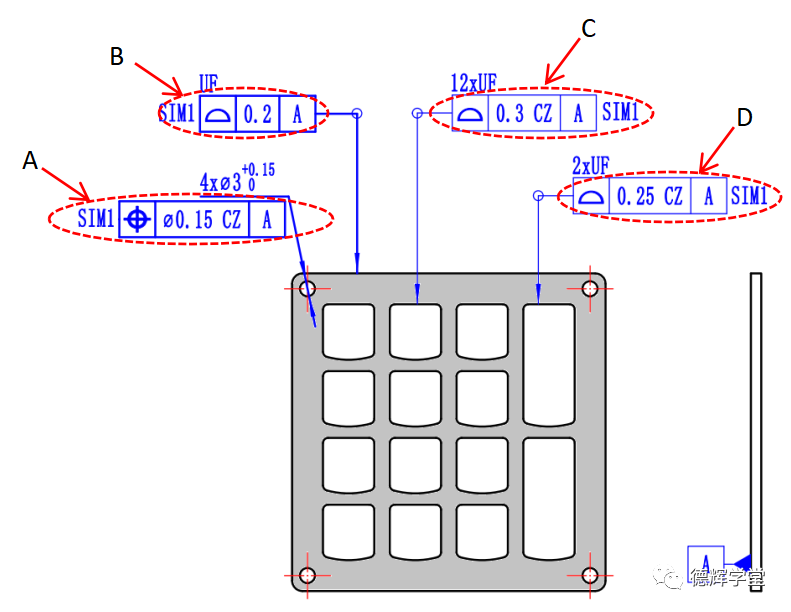
图17 键盘面板标注

图17就采用了SIM来控制，图中A,B,C,D这4个几何公差的公差带不仅仅要和基准保持关系，相互之间也必须保持理想的方位关系。尽管A,B,C,D这些几何公差的公差带大小，形状都不相同，但是作为人民群众，都必须团结一致，相互之间的方位关系必须绝对理想。见图18：

图18 相互关系（方位）绝对理想的公差带

图18中的所有的红色公差带相互方位关系绝对理想。这样控制，也就把四个圆孔（A），周边轮廓（B），12个方按键孔（C）和2个矩形按键孔（D）的相对位置都控制起来了，就能保证键盘面板和PCBA顺利装配。

能够控制不同特征之间的相对位置关系，是SIM的最大亮点，图18就是一个很好的说明！

另外需要说明的是，有时候，我们会看到图纸上会采用SIM1, SIM2，后边带数字的标注，这个很简单，就是归类，分团伙。比如“SIM1”表示所有带“SIM1”标记的几何公差是一个团伙的，他们内部公差带之间必须保持理想的方位关系；而所有带“SIM2”标记的几何公差属于另外一个团伙，同样，内部公差带相互之间保持理想的方位关系。

但是， “SIM1”团伙的公差带和 “SIM2”团伙的公差带相互之间没有任何关系，两个团伙的公差带不需要保持某种关系。

因为篇幅原因，本期文章先到这里，下次我们再继续探讨后边的章节，希望本期文章对你有所收获。

本章小结:

本期文章一开始我们构建了一个“鸟笼模型”来探讨几个关系：

1. 公差带和被测要素的关系（鸟笼和小鸟的关系）；

2. 公差带和基准的关系（鸟笼和晾衣杆之间的关系），即形成的外约束；

3. 公差带和公差带之间的关系（鸟笼和鸟笼之间的关系），即形成的内约束；

而本期的文章重点探讨的第3点，内约束。基于ISO5458：2018标准，内约束的标志有3个修饰符号，CZ, CZR和SIM，本文一一进行了讨论。

1. CZ，术语叫“组合公差带”，应用在“2x”，“3x”的几何公差，即当设计者用一个几何公差控制多个相同的特征的时候。要求公差带和公差带之间保持理想的方位关系（重要的事情说3遍，方位，方位，方位）。所以CZ是强调相同公差带之间的关系（用来固定相同的鸟笼的那个连接杆）。

2. CZR，术语是“仅约束方向的组合公差带”，同上，也是应用在一个几何公差控制多个相同特征的时候，要求公差带和公差带之间保持理想的方向关系（注意，仅方向，仅方向，仅方向）。所以CZR也是强调相同公差带之间的关系（用来固定相同的鸟笼的连接杆，只是连接杆上加了一个像天线一样的伸缩机构，只控制方向，不控制相互距离）。

3. SIM, 术语是“同时要求”, 和CZ和CZR不同的地方在于，它应用在多个几何公差，放在公差框的前后，表示这些几何公差的公差带相互之间要保持理想的方位关系（又是方位，方位，方位）。所以SIM针对的是多个几何公差的公差带，这些几何公差可以相同，可以不同。（用来固定不同的鸟笼，当然也可以固定相同的鸟笼的那个连接杆）。

内约束的本质是什么？

内约束针对的是多个特征（两个或两个以上），它的本质是就是想控制特征和特征之间的相互关系！

当然，对于好学的小伙伴来说，问题远远没完，比如：

1. 设计工程师如何根据功能选择内约束和外约束？

2. 美标（ASME）的内约束和外约束如何体现？

3. 内约束和外约束对测量评价有什么影响？

4. 采用了内约束后，对检具有什么影响？

5. 采用了内约束后，对工艺有什么影响？

这些问题都是我们企业里的工程师必须要面对的。你的理解是什么？评论区里面发表您的看法吧。